例谈用波利亚“怎样解题”的提示语解高考题*——以重庆市2013年理科第22题为例

杨孝斌，罗永超

(凯里学院数学科学学院，贵州凯里556011)

美籍匈牙利数学家、数学教育家G·波利亚在他的《怎样解题》一书中，首先给出了著名的“怎样解题表”.在怎样解题表中，波利亚指出，首先“你必须理解题目”.并给出了帮助解题者理解题目的几个基本问题：未知量是什么?已知数据是什么?条件是什么?理解题意是解题的最重要的环节.波利亚曾多次指出“理解了题意，相当于解决了问题的一半”，“理解了题意，往往能直接找到问题的解法”.理解题意的提示语中最常用的也是最关键的提示语主要有“它是什么”、“它有什么性质”、“它能如何表示”.这里的它，涵盖了题目中的所有对象，包括每一个已知量，每一个未知量，每一个式子，式子中的每一个符号，每一个符号的上标、下标，每一个图形，图形中的每一个元素等等.理解了题目中的所有的“它”，弄清了每一个“它”的性质，并找出这些所有的“它”之间的相互关系，就理解了问题，走出成功解决问题的第一步.

除了理解题意的提示语之外，“盯住目标”、“回到定义去”、“你以前见过它吗”、“有什么方法可以利用”，等等诸如此类的，是解题常用的提示语，以下把这些提示语统称为“怎样解题”的提示语.下面我们尝试用“怎样解题”的提示语来解重庆市2013年高考数学的第22题，此题是试卷的最后一题，即所谓的“压轴题”.

真题回放(重庆市2013年理科第22题)：对正整 数 n，记In= {1，2，…，n}，Pn=.试求：(I)求集合P7中元素的个数；(Ⅱ)若Pn的子集A中任意两个元素之和不是整数的平方，则称A为“稀疏集”.求n的最大值，使Pn能分成两个不相交的稀疏集的并.

此题新颖有创意，与以往压轴题的命题风格完全不同，题目有较大的开放度和灵活性，重点考查学生灵活运用分类讨论、反证法、构造法等几种重要的数学思想方法进行探索、分析与解决问题的综合能力，是一道以能力立意的好题目.该题虽有一定的难度，但所涉及的主要是一些基本概念、基本知识和常用的数学思想方法，同时考察学生对“新定义”的理解.下面我们尝试用“怎样解题”的提示语来分析并解决此题.

问题(I)：盯住目标!求什么?集合P7中元素的个数.

如此看来，问题(I)关键在于对Pn的理解，如果读不懂题，看不懂这个集合中的元素构成，实在是难以入手.同时，运用观察法对特殊值的考察也是考点之一.此外，对Pn的理解也直接影响到问题(Ⅱ)的解决，这充分说明了理解题意的重要性.

问题(Ⅱ)：盯住目标!求什么?求n的最大值.

n的最大值与谁有关?要满足什么条件?使Pn能分成两个不相交的稀疏集的并.分成两个不相交的集合的并，是什么意思?Pn=A∪B，且A∩B=φ.对A与B还有什么要求?A与B是稀疏集.稀疏集是什么?这个概念以前从未见过，题目里面是如何定义的?若Pn的子集A中任意两个元素之和不是整数的平方，则称A为稀疏集.也就是说，这里定义的稀疏集是Pn的子集，并且满足这个子集中的“任意两个元素之和不是整数的平方”.

接下来怎么办?考虑什么?根据问题(I)的解答，考虑Pn的元素构成.很容易看出In⊆Pn，而Pn=A∪B，且A∩B=φ，同时要求A与B是稀疏集，也就是集合A与B均要满足“其中任意两个元素之和不是整数的平方”.这里提到In，In是什么?In中的元素有什么特点?根据条件In={1，2，…，n}，In中的元素就是前n个正整数.

现在怎么办?从哪里入手?从最简单的情形入手，由于In⊆Pn=A∪B，不妨试试从前n个正整数入手.不妨设1∈A，因为1+3=22，故3∉A，于是3∈B，同理6∈A，10∈B，于是有15∈A，但是1+15=42，这与A为稀疏集矛盾.

这个结论说明了什么?当n≥15时，由于{1，2，3，…，15}中的元素不能全部放在两个稀疏集中，故In中的元素不能全部放在两个稀疏集中，因而Pn不能分成两个不相交的稀疏集的并，因此n最大不超过14.

下面考虑n=14的情形.当n=14时，有.

这样就可以了吗?问题到这里，到底想干什么?目标是什么?现在要考虑的问题是P14能否分成两个不相交的稀疏集的并?也就是寻找稀疏集A与B，满足P14=A∪B，且A∩B=φ.现在我们该怎么办?从哪里入手?仍然从简单的情形入手，首先考虑P14中的整数，其次是P14中的两个数的和为整数的情形，我们已经将P14进行了上述分解.此时我们要重点关注那些使为整数或分数的k的值，也就是k=1，4，9的时候的情形.因为如果k≠1，4，9，且k∈{1，2，…，14}，很显然有均为无理数，且这些元素与P14中的其它任何数之和都不是整数.

接下来我们该怎么办?分情况讨论.下面分四种情况讨论并最终解决问题.

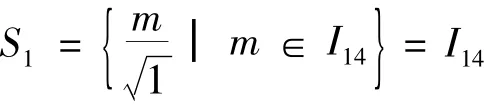
即I14)，剩下的元素组成的集合记为 S′4=，根据稀疏集的要求，可令，则A2，B2均为稀疏集，且A2∪B2=S′4.③同理，当k=9时，，去掉其中为整数的那些数(因为它们都属于S1即I14)，剩下的元素组成的集合记为，根据稀疏集的要求，可令，则A3，B3均为稀疏集，且 A3∪B3=S′9.④当k≠1，4，9，且k∈{1，2，…，14} 时，令.因此，集合C中的元素均为无理数，且这些元素与P14中的其它任何数之和都不是整数.

综上所述，令A=A1∪A2∪A3∪C，B=B1∪B2∪B3，根据上面的构造过程知，A与B均为稀疏集，并且满足P14=A∪B，A∩B=φ.因此，当n=14时，有P14能分成两个不相交的稀疏集的并.所以，n的最大值为14.

以上是利用波利亚“怎样解题”的提示语解数学题的一个实例，从上述过程可以看出，利用“怎样解题”的提示语解数学题，可以帮助学生弄清问题中的各个元素，从目标入手，找到已知量、未知量之间的联系，逐步深入问题的核心，从而解决数学问题.这些提示语，看似平淡无奇，但由于它们均是从问题中基本元素的定义和性质出发，层层深入、步步逼近问题的核心.因此，这些提示语在解题中的成功运用，往往能帮助学生抓住问题的本质，在解题过程中化繁为简、化难为易.

在数学教学中，教师可以尝试用“怎样解题”的提示语开展教学，利用这些提示语帮助学生理解题意、弄清问题、找到问题的解决办法.学生在教师的示范和引导之下，能够学会用“怎样解题”的提示语解数学题，并将其逐步内化，最终发展成为自己的解题提示语.

［1］(美)G·波利亚.怎样解题［M］.涂泓，等译.上海：上海科技教育出版社，2011.

［2］杨孝斌.数学教学思维导向的研究［M］.成都：四川大学出版社，2010.