注重方法形成过程 促进课堂智慧生成

●

(通州区兴仁中学 江苏南通 226371)

笔者有幸执教了一次初三中考数学总复习的公开课，授课时对等边三角形例题教学方法的探究受到当时听课专家的高度评价：“注重方法，智慧生成”．现结合笔者的课堂教学经验谈谈对学生解题方法形成的一点认识与思考，以抛砖引玉．

1 问题再现与初解

已知：等边△ABC的边长为a．

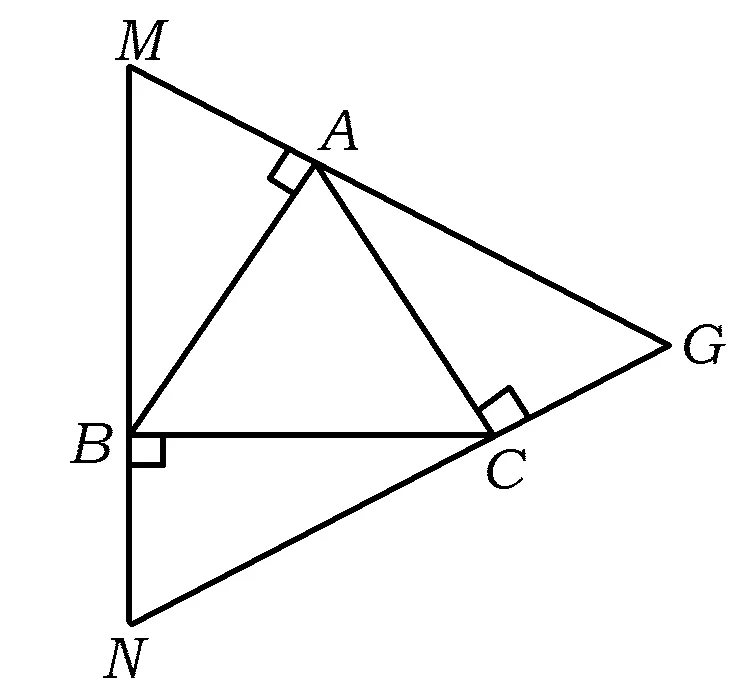
图1

探究2在等边△ABC内取一点O，过点O分别作OD⊥AB,OE⊥BC,OF⊥CA,垂足分别为点D,E,F.

(1)如图2，若点O是△ABC的重心，我们可利用三角形面积公式及等边三角形性质得到2个正确结论(不必证明)：

(2)如图3，若点O是等边△ABC内任意一点，则上述结论1和结论2是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．

图2 图3 图4

课前批阅作业发现，学生对于探究1会证明，对于探究2中的问题(1)也容易理解，对于探究2问题(2)中的结论1，学生初始解法是这样的(面积法)：如图4，联结AO,BO,CO，过点A作AH⊥BC于点H，由

S△ABC=S△AOB+S△BOC+S△AOC=

而

故

对于问题(2)中的结论2，学生开始没能做下去．课后询问学生了解到他们也想到与探究1有关，可能会用到前面的结论，但就是不知道如何联系起来.

2 教学片断及评析

2.1 在数学方法形成前，为其铺路引桥

课堂教学总是在“预设”与“生成”间交融进行.学生从接触探究(1)到解决探究(2)，特别是探究(2)的结论2，有一个较长的过程.这是由学生的认知水平和问题本身的难度所决定的.教师要明了其间的巨大落差，给学生充分的思考与讨论时间，在原有认知和现存问题之间合理设置阶梯，架设桥梁，帮助学生搭建解决问题的“脚手架”，让学生“跳一跳，就能摘到桃子”，在“最近发展区”不断完善自己的认知水平，提升思维品质.

图5

教学片断1(基于作业批阅)

师：我们先复习这样一个拓展问题：如图5,在△ABC中，AB=AC，D是底边BC上任意一点，DE⊥AB,DF⊥AC,CG⊥AB,垂足分别为E,F,G，则DE+DF与CG有何数量关系？请说明理由．

生1：DE+DF与CG的数量关系是DE+DF=CG.用面积法可以证明，联结AD，根据S△ABD+S△ACD=S△ABC很快可以证明DE+DF=CG．

师：如果点D是等边三角形一边上的点,其他条件不变，有同样的结论吗?

生(齐答)：当然有！

师：如果点D是等边三角形一边上的点,将CG这条高改为任意一边上的高，其他条件不变，有类似的结论吗?

生(稍作思考)：有！

师：请大家先独立思考然后小组内讨论，看哪个小组能首先证明探究2中问题(2)的结论1.

学生思考、讨论后,有学生回答.

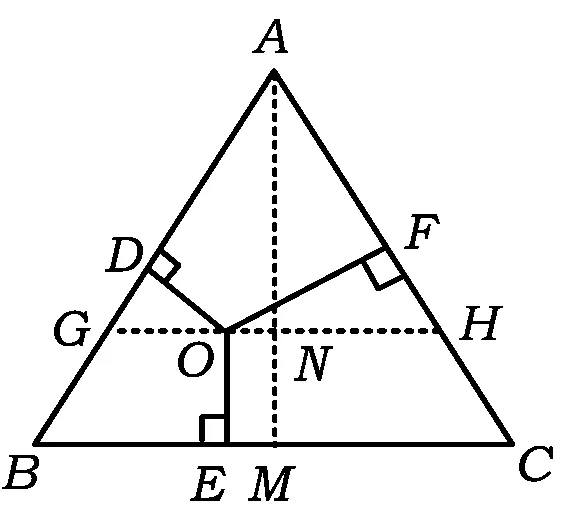
图6

生2：我们小组讨论出方法了，如图6，过点O作GH∥BC交边AB,AC于点G,H，过点A作AM⊥BC垂足为点M，交GH于点N，显然由上面的结论可得OD+OF=AN，从而

得证(转化法1).

笔者通过批阅学生作业时发现学生能轻松解决探究1，但对探究2存在疑惑，教学时没有急于直接向学生讲解，而是“反其道而行之”，先引入了拓展问题，让学生思考、讨论、合作分析，发挥集体智慧，为解决探究2成功地铺好道路，进而引发了学生对探究2中问题(2)的结论1证明的思考.正如预设那样，有了“转化法1”，顺利得到“智慧”的“生成”.

2.2 在数学方法形成时，将其化隐为显

心理学研究表明，学生的认知角度、数学方法的形成要经历潜意识阶段、明朗阶段、形成阶段和深化阶段.因此，学生头脑中的数学方法形成过程，实质上就是在新旧知识的认知冲突中探究与发现的过程.如果学生在此过程中未能突破，就迫切需要教师以典型的范例将其化隐为显.教师要及时促进学生对问题或其解答进行加工，并引导学生对问题解答进行自我解释，从中抽取出数学方法.

教学片断2

师：你觉得刚才解决问题的关键是什么?

生3：根据“等腰三角形底边上任意一点到2腰的距离之和等于一腰上的高”和“等边三角形3条高相等”添加了辅助线，将3条垂线段转化成等边三角形的高.

师：不错！等边三角形可以分解为特殊直角三角形，掌握这一性质对解题很有帮助！

生5：我们在解决探究1时就已经用了这一性质.

师：对！有没有发现图中有其他这样的直角三角形？从中你能看出对结论有什么帮助吗？请大家在小组内讨论，然后交流.

生6：利用这一性质不仅可以证明结论1，而且可以证明结论2.

图7

AD+BE+CF=

得证(转化法2).

图8

生7：将“过点G作GM⊥BC垂足为点M”改为“过点O作OM∥AB交BC于点M”(如图8)，又得到另一证法(转化法3)……

生8：过点O作其他平行线或垂线段还可以得到“转化法4”……

(与“转化法2”类似的一系列“转化法”，这里不再赘述.)

学生想到“转化法1”时，追问此方法的关键是什么；学生认识到等边三角形转化成直角三角形，利用特殊直角三角形的性质时，进一步追问这一性质对解决本题有何帮助，这样学生对问题的认识逐渐清晰，方法就逐渐明确化，进而产生了“转化法2、转化法3、转化法4”等一系列“转化法”.这时绝大多数学生对问题的理解趋向深刻，能从更高的层次、更新的角度进一步掌握、理解等边三角形的有关知识技能.不仅有利于学生形成良好的数学思维习惯，而且在解决问题过程中形成更高层次的数学思维能力.

2.3 在数学方法形成后，将其优化提升

作为教师，首先不仅要明确本题不止一种解法，而且要清楚哪一种解法最适合；其次，在了解学生完成一种解法后，应引导学生探求一题多解，并对方法作比较；第三，要引导学生对数学学习过程进行反思，总结解题思路，提炼数学方法，揭示问题本质，提升解题能力，进而不断生成智慧.

教学片断3

师：不同的解法来自于深入的思考，还有其他证明方法吗？

(学生沉默了一会.)

生9：我利用勾股定理得到AD2+OD2=AO2,BE2+OE2=BO2,CF2+OF2=CO2,但是下面好像不好做了，但是我觉得应该行得通.

师：是一种好的思路！实际上你是想利用勾股定理把线段AD,BE,CF之和转化为线段OD,OE,OF之和(如图4)，可知

AD2+OD2=AO2=AF2+OF2,

BE2+OE2=BO2=BD2+OD2,

CF2+OF2=CO2=CE2+OE2,

上述3个式子相加后整理可得

生：果然行！

图9

师：老师课前认真查阅过许多资料，发现有一本杂志上用了“旋转法”：如图9，由旋转的知识可以直观地看出结论是成立的,大家认为这一方法可行吗？

生10：可以是可以的，但过程不容易书写.

由BM=OG=GP,CH=BG可得

AP+BM+CH=AB.

再由

和

AD=AP+DP,BE=BM+ME,CF=CH+FH，

可得

图10 图11

又OF′=AD,OD′=BE,OE′=CF，从而

生：(惊叹)还可以这样！

师：请大家对这几种方法做一下比较，哪种方法最优？优点在哪里？

笔者认为“旋转法”虽然欠妥但它能引起学生的顿悟.实际上，学生能立即发现“转化法5”显然优于此法.利用勾股定理的方法步骤比较繁琐且对计算的要求也高，利用结论1的方法很难想到，对少数尖子生可以引导其思考，体现了“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”这一数学课程的总目标，同时还开阔了学生的视野，拓展了学生的思维，又将知识融会贯通，使初三数学总复习达到了综合、优化、提升的目的.

通过对问题多种解法的思考、比较，学生的学习兴趣将大大增加，思维能力将得到有效提升.通过解题后的反思，将会形成层次更高的经验，为进一步学习解决问题的最优化作准备.这样，学生掌握的不仅是一道题的解法，而是其本质；收获的不仅是知识，更有兴趣和智慧.