不等式恒成立问题参数范围的确定
●
(黄湾中学 安徽灵璧 234213)
对于不等式恒成立问题,参数范围的确定是一种较为常见的问题,主要表现为以下几类:(1)在给定区间上不等式恒成立;(2)不等式的解集为全体实数;(3)解析式的值恒大于(等于或小于)某值;(4)函数的定义域为全体实数.由于此类问题知识覆盖面较广,综合性很强,对解题的灵活性要求高,因此对学生来说有较大的难度.其实,若能灵活利用知识,对于不等式恒成立问题,其参数范围还是容易确定的.
1 利用一次函数的保号性
若原题可转化为一次函数型,则可利用一次函数的保号性求解,过程将会变得简捷.
例1已知y=(log2x-1)(logab)2+log2x-6log2x·logab+1>0(其中a>0,a≠1),当x∈[1,2]时,y的值恒为正,求b的取值范围.
解由
y= (log2x-1)(logab)2+log2x-6log2x·logab+1=
[(logab)2-6logab+1]log2x-(logab)2+1.
设t=log2x,x∈[1,2],则
y=f(t)=[(logab)2-6logab+1]t-(logab)2+1,
其中t∈[0,1],于是该问题转化为当t∈[0,1]时,f(t)>0恒成立,求b的取值范围.由
解得
故当a>1时,
当0 即 亦即 从而 解得 例3不等式(a2-1)x2-(a-1)x-1<0对x∈R恒成立,求实数a的取值范围. 解(1)当a=1时,-1<0,不等式恒成立;当a=-1时,不等式对x∈R不恒成立. (2)当a2-1≠0时,有 解得 综上可得 ( ) A.-7 B.6 C.7 D.8 2-ax-x2<3(1-x+x2), 即4x2+(a-3)x+1>0对任意x∈R恒成立,故 Δ=(a-3)2-16<0, 解得 -1 由题意知t1+t2=-1+7=6.故选B. 若原题较容易分离出变量,而令一边为常见函数,则可转化为这些常见函数的最值问题求解. 例5若不等式sin2x+2acosx-a2+2a-3<0对任意实数x∈R恒成立,求a的取值范围. 解原不等式可化为 cos2x-2acosx+a2-2a+2>0, 设t=cosx,则 f(t)=t2-2at+a2-2a+2= (t-a)2-2a+2, 其中t∈[-1,1],从而问题等价转化为f(t)>0在t∈[-1,1]上恒成立,即f(t)在t∈[-1,1]上的最小值大于0. 于是a的取值范围为(-∞,1)∪(3,+∞). 例6设函数f(x)=ax2-2x+2对1 解由题设得 即 适当地引进新变量进行代换,可以简化原题的结构,实现问题的转化和变通. 解由f(x)是奇函数,知 f(-2)=-f(2), 则 f(sin2x-msinx+m)>f(2). 又f(x)是减函数,知 sin2x-msinx+m<2, 令sinx=t,则0≤t<1,从而 t2-mt+m<2, 即 m(1-t)<2-t2, 解得 [g(t)]min=g(0)=2, 从而 m<2. 例8已知实数x,y满足x2-2x+y2=0,求使x+y+k≥0恒成立的实数k的取值范围. 解将x2-2x+y2=0化为 (x-1)2+y2=1. 因为 分析本题若直接求解难度会很大,为此可从简单情形入手: 当n=2时,满足条件的m的取值范围为m≤41; 当n=3时,满足条件的m的取值范围为m≤44; 当n=4时,满足条件的m的取值范围为m≤45; …… 为此有如下猜测:m的取值范围为m≤41. 改变观察和思考问题的角度,采用数形结合的方法求解不等式恒成立中参数的范围,能使问题化抽象为直观,取得避繁就简的效果. 例10若|x+3|+|x|≥m对任意x∈R恒成立,求m的取值范围. 分析显然只要求得|x+3|+|x|的最小值即可,而|x+3|+|x|的几何意义是数轴上到-3的点的距离与到原点的距离之和,此和的最小值从数轴上不难知道是3,故m≤3. 图1 对于有些不等式恒成立求参数取值范围的问题,由于综合性强,涉及的知识点多,在求解时,需要综合利用各方面的知识,找到多种求解方法.这有利于提高我们思维的灵活性和创新能力. 例12已知不等式2x2-9x+m≤0在区间[2,3]上恒成立,求m的取值范围. 解法1(解不等式)根据题意,不等式的解集非空,Δ≥0,此时解集为 故 解得 m≤9且m≤10, 故 m≤9. 点评求出不等式的解集,根据解集与给定区间的关系列出含有参数的不等式或不等式组,从而获解.这是一种常规思路,求解过程通常较繁琐. 解法2(讨论方程的根)根据题意,方程2x2-9x+m=0有实根,且2个根分别在区间(-∞,2],[3,+∞)上. 设f(x)=2x2-9x+m,则f(2)≤0且f(3)≤0,从而m≤9且m≤10,故m≤9. 点评不等式的解往往与方程的根有联系,不等式的解集中的端点常常是对应方程的根,因此当原不等式为二次不等式时,应与韦达定理、实根分布相联系. 解法3(函数的最值) (1)从数的角度看. 方法1设f(x)=2x2-9x+m,x∈[2,3],问题等价于f(x)max≤0,而 得 m-9≤0, 即 m≤9. 方法2(分离参数法)问题等价于不等式m≤-2x2+9x在区间[2,3]上恒成立. 设g(x)=-2x2+9x,x∈[2,3],则问题等价于m≤g(x)min,而 即m≤9. (2)从形的角度看. 方法1当x∈[2,3]时,f(x)=2x2-9x+m的图像始终不高于直线y=0,也就是函数f(x)=2x2-9x+m的图像的最高点在直线y=0的下方或者在该直线上,即f(3)≤0,从而m≤9. 方法2(分离参数法)问题等价于不等式m≤-2x2+9x在区间[2,3]上恒成立. 点评通过对该例(最常见的恒成立问题)的一题多解,揭示了含参数不等式恒成立问题实质上体现了函数、方程、不等式之间的有机联系.因此求解此类问题常常从不等式的解、方程的根、函数的最值这几个方面入手,结合图形,灵活转化,选择最佳解题策略.
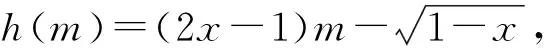

2 利用二次函数的判别式

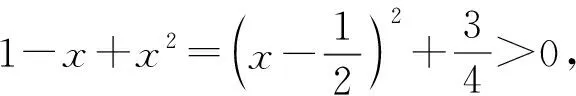

3 分离参数利用函数的最值





4 设参引元,利用函数的单调性




5 先探索猜测,再证明

6 以形代数,化抽象为直观


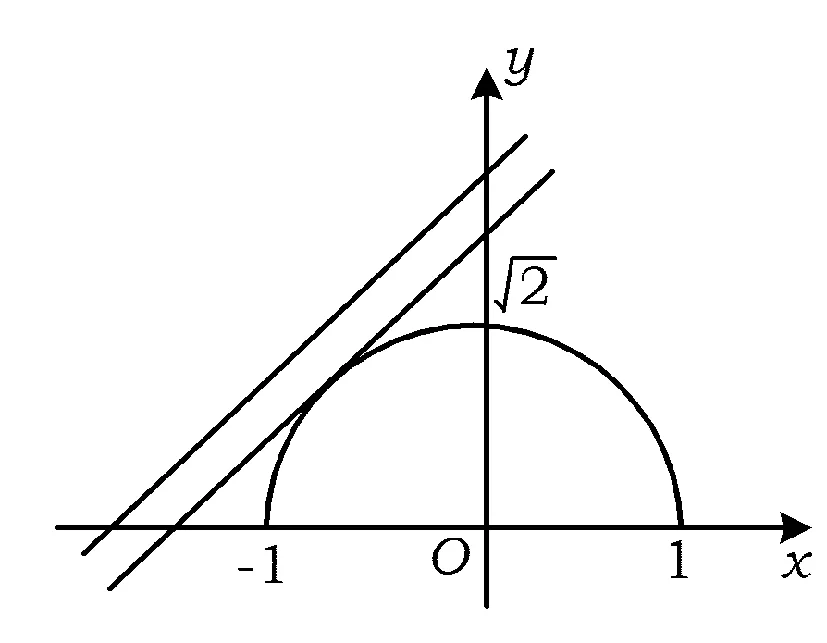

7 多法并用,一题多解



