社区公交接驳地铁路径优化研究

熊 杰,关 伟,黄爱玲

(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044)

社区公交接驳地铁路径优化研究

熊 杰,关 伟*,黄爱玲

(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044)

社区公交在公共交通运输服务体系中起着重要的微循环作用,其路径的优化问题对于出行者及运营企业均具有重要意义.本文在给定的路网条件下,首先从路段角度定义了路段的需求潜力指标,并以最大化路径需求潜力为目标建立目标函数,并兼顾路径旅行时间及圈点线路约束建立了求解一条圈点线路的数学模型.在求解过程中,本文设计了一套路段交叉变异算法并利用遗传算法实现了模型的启发式求解.最后,本文以北京天通苑社区为例,利用该社区居民的出行数据并分别应用遗传算法及深度优先搜索算法对服务于该社区的公交路径进行优化设计.实验结果表明,遗传算法在该实例中已得到最优解,证明遗传算法在求解该问题上具备可行性.

综合交通运输;路径优化;遗传算法;社区公交;接驳;地铁

1 引 言

近年来城市近郊大型社区规模不断扩大,衍生出大量地铁出行需求,不同交通方式间的换乘问题也日益显著.而社区公交由于其自身机动、灵活的特点,在公共交通系统中起着不可替代的微循环作用.因此对社区公交开行路径进行优化,以使其能够更好地与地铁相接驳,对于提高公共交通系统的整体运营效率以及降低社区居民出行成本都有着重要意义.

在过去几十年中,国内外许多学者都对类似于社区公交服务性质的机动班车的行车路径进行过大量研究.机动班车路径的优化研究依赖于特定的路网结构条件,以往文献中对于路网结构的设定主要分为三种情况:基于简化的路网结构、半现实路网结构,以及现实路网结构.基于简化的路网结构往往将路网简化为由若干条水平与竖直的道路构成,进而设计出一条或多条相互平行的班车路径. Chang 和 Schonfeld[1]提出了在一个简单的长方形服务区域内设计班车路径问题,并指出多对一的需求模式对于服务质量和费用都具有一定弹性; Chien 和 Schonfeld[2]提出了一种用于优化一条铁路线路与 多 条 公 交支 线相 互换 乘的 模型;Chien等[3]比较了服务于一个矩形区域的固定和灵活支线服务,并得出最好的方案为在高峰时期运行传统班车服务,而在非高峰时期运行机动支线服务.类似文献还可参见 Chang 和 Lee[4],Chang 和 Yu[5].

基于半现实路网结构的班车路线优化问题所给出的服务区域大多为不完全网格结构,而班车开行路径必须沿可行驶路段进行延伸,因此最终生成的班车路径往往并非一条直线,也打破了简化路网结构下线路间相互平行或垂直的格局.Chien[6], Chien 等[7]设计了一种网格状路网条件下服务于综合交通换乘中心的公交支线的生成方法,并考虑了地理条件、客流量及预算限制等约束条件; Ceder[8]提出了班车的潜在需求指标这一概念,并以需求指标最大化为原则建立模型,之后应用分阶段、多目标的原则设计了一套班车管理运营系统,并从智能化、可视化等方面对系统进行了检验.

基于现实路网结构的班车路线优化问题完全以实际路网为基础,在处理该类问题时,一般先将路网节点进行编号,而后进行路段间关联性分析,进而将节点按照一定顺序相连接形成可行解,之后一般根据目标函数的表达形式并通过遗传算法搜寻近似最优解.Fan 和 Machemehl[9]对可变需求下公交路径优化问题的潜在特性进行了较深入分析,并提出了一种多目标非线性混合整数规划模型; Shrivastava 和 Mahony[11]对接运于某一火车站的若干条公交支线进行了路径及行车时刻表的优化研究,并根据已有火车运行时刻表对接运公交支线的发车间隔进行调整,最终同时生成了优化的公交路径及时刻表.类似文献还可参见Shrivastava 和Dhingra[11-12].

本文以现实路网条件为基础,在对给定路网下具体路段进行分析时,定义了路段的需求潜力指标.在建模过程中,以最大化整条路径的需求潜力为目标,兼顾路径走行时间约束与圈点线路的特征条件约束,构建了一种求解圈点线路的数学模型.在模型求解中,利用 GA 的算法思想并对选择、交叉及变异算子进行了设计,实现了模型的求解.最后,利用通过手机基站得到的天通苑社区内部早高峰出行 OD 数据,对该区域内进行了圈点线路的优化设计,证明了模型与算法的可行性.

2 模型建立

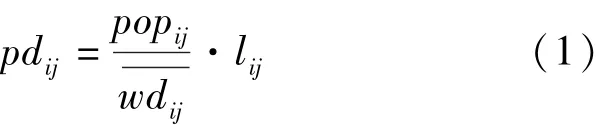
社区公交线路设计原则应为,尽可能用较短的线路走行时间搭载尽可能多的旅客到达相邻的地铁站点.本文以路段为研究对象,并针对路段定义了路段开行公交的潜在需求这一指标,如式(1)所示:式中 pdij为 路 段 (i,j) 开 行 公 交 的 潜 在 需 求; popij为路段 (i,j) 所集结的出行需求;为路段(i,j) 所吸引的乘客至该路段的平均距离;lij为路段 (i,j) 至接驳站点距离,本文假设其为路段中点至接驳站点的直线距离.

由式(1)可知,路段潜在客流需求与相应集结区内出行需求、路段至接驳站点距离成正比(由于路段距地铁站点越远,乘坐公交出行需求越大),而与集结区内乘客步行至该路段的平均距离成反比.

另外,为方便计算区域内各路段所集结的客流需求 (popij)及各路段对应的乘客平均距离,需首先对研究区域进行交通出行小区划分.交通出行小区为具有一定出行关联度和相似度的节点集合,且随时间、关联度和相似度的变化而变化,它反映了该区域内居民出行的特征.本文对研究区域进行小区划分正是为了利用小区内出行具有关联度及相似度的特性,方便地将区域内客流需求匹配至相应路段.而区域的小区划分情况势必会决定客流匹配结果,进而对本文后续计算产生重要影响,在实际工程操作中,应按以下原则对区域进行出行小区划分:

(1)同质性与稳定性.同一出行小区内部应尽量具有相似的出行特性,如相似的出行强度、交通状态等,且各小区的出行情况不会随时间出现频繁变动,应保持相对稳定或呈现周期性变化规律.

(2)小区的面积及数量应适当.如分区过大,则同一区域内的出行需求很难被集计加载至某一特定路段,反之则会加大计算的繁复程度,失去出行小区划分的意义.因此需结合区域内道路网的具体情况及客流走行距离综合考虑小区的划分情况.

(3)控制区内出行的比例.由于区内出行数据无法被分配到路网,因此过高的区内出行比例将使分配结果无法真实反映区域出行情况,原则上,区内出行比例应控制在 5%-15%.

(4)当区域内存在地铁站、大型公交枢纽站点时,应尽量保证这些设施处于相应出行小区内部,避免被不同小区分割.

基于上述原则,在实际出行小区划分时,首先应对区域内居民出行情况进行充分调查,调查对象为去往相应地铁站的居民,掌握其到达地铁站前的出行信息;之后可利用空间聚类分析的方法将具有相似出行特性的个体划定在同一出行小区之内,进而实现区域内出行小区的划分.本文为简化起见,将研究区域进行网格化处理,即将每一网格视为一个交通出行小区,如图1 所示,并提出如下假设:

(1)同一网格内的乘客均被匹配至同一路段,不同网格的乘客可分配至不同路段;

(2)各网格内乘客至匹配路段的距离为从网格中点至相应路段的最短距离.

基于此,本文利用 Logit模型将各网格内的乘客分配至区域内唯一路段,分配概率如式(2)所示:

式中 P(k,ij) 为网格 k 被分配至路段(i,j) 的概率;为网格k内乘客匹配至路段(i,j) 的距离;A为区域内路段集合.

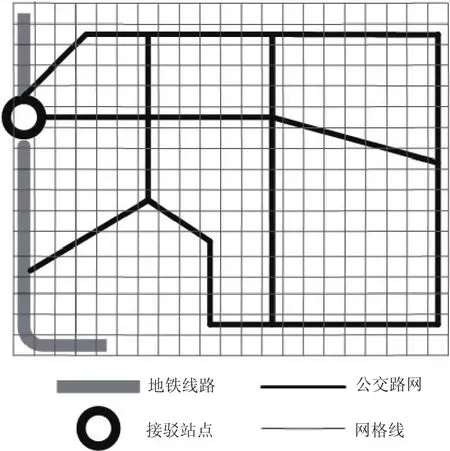
图1 研究区域示例Fig.1 Example of study area

因此,按照式(2)可将各网格分配按照一定概率至区域内唯一路段,进而求得各路段所吸引的客流量及所对应平均匹配距离:式中 popk为网格 k 内客流需求;U 为区域内所有网格集合. 如果网格 k 被分配至路段(i,j),则f(k,ij)= 1,否则 f(k,ij)= 0.

在路径生成方面,本文借鉴 Ceder[13]中生成一条圈点线路的模型,设 G={N,A} 表示某区域内路段集合,N表示节点集合,A 表示路段集合.而每条路段 (i,j) 都对应一个平均旅行时间 tij和需求潜力指标 pdij.求解模型可产生一条开始并终止于接驳地铁站点 n1的圈点线路.该模型可使乘客的潜在需求量达到最大,同时又满足最大旅行时间T的限制,因此模型描述如下:

约束条件:

式(6)表示线路最大旅行时间约束;式(7)-式(8)为在路网中新建一条圈点线路的限制条件,式(7)表示进出每个节点的路段数量守恒,式(8)保证了线路闭合;式(9) 中 yij=1 表示路段 (i,j) 为路径的一部分,反之 yij=0.

3 遗传算法求解

在应用遗传算法(GA)求解路径前,首先将实际路网拓扑为仅由若干水平及竖直道路组成的简单路网.而由于圈点线路具有起止于同一点且闭合的特性,因此在生成道路时可将拓扑后的路网以某边界为轴进行对称操作,之后按照一定顺序(如从左至右)对线路进行生成.例如图1 中路网可拓扑并以右边界为轴进行对称,得图2所示路网.

图2 路网拓扑结构图示例Fig.2 Example of the topological structure of network

在图2所示路网条件下,社区公交的开行路径只能沿实线进行延伸,本文规定路径的生成方向为由左至右,因此可将路段中各节点按照所能提供的走向不同进行分类并赋值.具体情况如图3所示,可将路网中所有节点按照所能提供走向的不同分为8 种情况,并分别赋予 0-7 中的一个数值,且每种情况唯一对应一种线路走向集合,线路的基本走向分为向上、向右、向下 3 种,分别赋予数值 1,2, 3.因此,由路径的生成表示法得到的最终路径表达形式为由数字 1,2,3 组成的长度不定的矩阵.例如,图2中路网及路径矩阵如图2中所示.

图3 节点及走向赋值情况Fig.3 Assignment of nodes and directions

上述方法可对给定拓扑路网下任意路径进行表示与生成,因此为遗传操作打下基础.之后,直接以线路矩阵 route 作为染色体进行选择、交叉与变异操作.在遗传操作中,适应度函数直接选取为模型目标函数,并采用轮盘赌思想,即个体被选择概率与其潜在客流需求成正比.假设种群规模为NIND,遗传代沟为 GGAP, 第 i 个个体适应度为pdij,则每个个 体 被选择 的概率最终选出 NIND′=NIND × GGAP 个个体进行后续的交叉与变异操作.

在交叉操作中,确定两条路径能在点O处交叉需同时满足以下4项条件:

(1) 两条路径至少存在一个公共点 O;

(2)两条路径在公共点 O 的前段与后段均不可完全重合;

(3)当两条路径在某竖直路段部分或完全重合而O点恰好位于重合路段上时,不可直接在O点进行交叉,需同时对一条子路段的末尾与另一条子路段的起始元素进行不断剔除,直至交叉后路段中不包含[1 3] 或[3 1] 子段为止;

(4)新生成路径应满足最大旅行时间约束,否则视两路径不可交叉.

交叉操作的具体步骤如下:

(1)设定交叉率 Pc,最大尝试交叉次数 Nm;

(2) 对变量 l 取 1 至 NIND′重复步骤(3)-(5);

(3)随机生成一个 0,1 之间的数 pick,若 pick≤ Pc,进行步骤(4),否则返回步骤(2);

(4)随机选取两条路径,按照一定顺序检验两路径公共点,判断各公共点是否满足上述 4项条件,若满足,则在该点进行交叉,返回步骤(2),否则尝试交叉次数加1,进行步骤(5);

(5)判断尝试交叉次数是否大于 Nm,若是,该循环下交叉失败,返回(2),否则返回(4).

在变异阶段,染色体均为代表线路的 route 矩阵,若随机改变其中某元素的值,会导致使新生成染色体无法再表示一条可行路径,因此在变异中采取重新生成新路径替换被选择路径的方法.具体步骤如下:

(1)定义变异率 Pm;

(2)对变量 l取 1 至 NIND′重复步骤(3);

(3)随机生成一个0,1之间的数pick′,若pick′≤ Pm,则随机生成一条线路,并检验该线路是否满足旅行时间约束条件,若满足,用该线路替换第 l条线路,否则继续随机生成线路直到满足条件为止.

最后将经过选择、交叉及变异后得到的NIND′个个体插入到父代中.插入时仍基于个体适应度大小对其进行插入,即新产生路径的潜在客流需求越大,则被插入到父代的概率越大,父代中路径的潜在客流需求越小,则被新路径替换的概率越大.最终仍得到 NIND 个个体作为子代,以保证种群规模不变.

4 实例分析

选择北京市天通苑社区为试验区域,地铁5号线垂直穿过该区域,并设地铁天通苑站为接驳站点.首先,利用该区域内手机基站的记录信息得到一天内各基站至接驳站点间的 OD 数据.该区域共被六个基站所覆盖,其编号分别为 683、684、658、659、660、661,各基站覆盖范围可参见图4.各基站信息如表1 所示(表中客流需求数据为 2012.2.3-2012.2.9 日全日 OD 数据并取平均,并假设产生或到达区域 683 的客流均为乘坐地铁客流,基站面积及出行数据均由中国移动提供).但由基站所划分的出行小区形状不规则且面积较大,很难细致地将出行信息加载至各路段,因此采用区域网格化的方法,将该区域划分为 20×20 个网格,每个网格实际代表一个 150 m ×120 m 的矩形出行小区,如图4 所示.

图4 天通苑社区基站分布及路网示意图Fig.4 Service areas of base stations and network of Tian TongYuan Community

表1 各基站辐射区域面积及出行需求Table1 Value of each service area and traffic demand

假设各基站内出行客流密度一致,结合表1数据与式(2),可计算得到各网格的路段匹配情况,各网格客流需求,以及各网格至路段的匹配距离.之后假定公交车运行速度为 14 km/h,得到各路段旅行时间.再利用式(1)、式(3)、式(4)计算得到各路段所集结的客流需求 popij,各路段所对应乘客的平均匹配距离,最终计算出各路段开行公交的需求潜力指标,相关数据见表2( 假设 pdij=pdji,因此表2仅记录单向路段各指标数值).

表2 各路段相关数据Table2 Some related data of each route segment

基于天通苑实际路网图建立拓扑路网图(现实路网中不存在的路段用虚线连接),之后以右侧边界为轴对拓扑路网图进行对称操作,并将潜在客流需求数据加载至相应路段,如图5所示.

图5 对称后的拓扑图及路段潜在客流需求指标Fig.5 Symmetrical topological structure and potential passenger demand of each segment

在进行遗传操作中,相关参数取值如下:种群规模 NIND=40,最大遗传代数 MAXGEN=20,代沟 GGAP=0.9,最大尝试交叉次数Nm=20,交叉率Pc=0.7,变异率 Pm=0.4,并设定最大旅行时间T=75 min,得到路径潜在客流需求迭代曲线,如图6所示.

图6 潜在客流需求迭代曲线Fig.6 Iterative curve of total potential passenger demand

如图6 所示,目标函数在遗传至第 10 代后趋于稳定,最大潜在客流需求值为 2 898.7 人.并同时得到相应路径的 route 矩阵为 route*=[3 3 2 1 2 2 2 1 1 2 3 3 3 2 1 1 2 2 3 2 3 2 1 1],相应拓扑图中的路径如图7所示.

同时输出式(5)中变量 yij的取值,如表3 所示.

图7 拓扑图中最优路径Fig.7 Optimal route in topological network

表3 yij取值列表Table3 Values of yij_

表3中,若 yij=1,则表明有向线段 (i,j) 为实际路网下最优路径的一部分,因此依照表3结果并结合图7,逆着拓扑图的生成方法可将拓扑图中最优路径还原至现实路网中,如图8所示.

图8 实际路网中最优路径Fig.8 Optimal route in realistic network

为证明遗传算法所得解的准确性,在拓扑路网下应用深度优先搜索算法(DFS)遍历所有可行路径,共生成路径 576 条(按照一定顺序),其中 565条满足最大旅行时间约束.对所有满足最大旅行约束时间的路径计算其潜在客流需求指标,并绘制成折线图如图9所示.

图9 利用 DFS 生成所有可行路径的潜在客流需求Fig.9 Potential passenger demands of all routes obtained by DFS

由图9可知,遗传算法所得最大目标函数值与遍历搜索所得值相等(均为 2 898.7),且相对应的最优路径相同,因此可认为遗传算法已在该实例中得到最优解.而遗传算法对于更大规模的路网在计算效率上也存在较大优势. ________________________________________________________________________

5 研究结论

本文首先定义了路段潜在客流需求指标,用以衡量某路段在某一区域内吸引乘客的能力,并基于此指标建立了求解一条最优圈点线路的数学模型.在模型求解中,首先提出了路网的变化方法及路径的生成方法,进而设计交叉与变异算子以实现遗传算法在路径优化问题上的求解.最后,通过实例证明了上述模型及算法的可行性,并通过遗传算法与深度优先搜索运算结果的比较,证明了遗传算法的准确性.而对于更加复杂路网情况下,遗传算法在解决路径优化问题上所能达到的精度及计算效率的提高程度则是今后研究的重点.

[1] Chang S K,Schonfeld P M.Multiple period optimization of bus transit systems[J].Transportation Research, 1991,25B:453-478.

[2] Chien S,Schonfeld P M.Optimization of grid transit system in heterogeneousurban environment[J]. Journal of Transportation Engineering,1997,123(1): 28-35.

[3] Chien S I,Spasovic L N,Elefsiniotis S S,et al. Evaluation of feeder bus systems with probabilistic time-varying demands and non-additive time costs[J]. Transportation Research Record,2001,1760:47-55.

[4] Chang S K J,Lee C J.Welfare comparison of fixedand flexible-route bus systems[J].Transportation Research Record,1993,1390:16-22.

[5] Chang S K,Yu W J.Comparison of subsidized fixedand flexible-route bus system[J].Transportation Research Record,1996,1557:15-20.

[6] Chien S.Optimization of headway,vehicle size and route choice for minimum cost feeder service[J]. Transportation Planning and Technology,2005,28: 359-380.

[7] Chien S,Yang Z,Hou E.Genetic algorithm approach for transit route planning and design[J].Journal of Transportation Engineering,2001,127:200-207.

[8] Ceder A.Stepwise multi-criteria and multi-strategy design of public transit shuttles[J].Journal of Multi-Criteria Decision Analysis,2009,16:21-38.

[9] Fan W,Machemehl R B.Optimal transit route network design problem with variable transit demand: genetic algorithm approach [J]. Journal of Transportation Engineering,2006,132(1):40-51.

[10] Shrivastava P,Mahony M O.A model for development of optimized feeder routes and coordinated schedules-A genetic algorithms approach[J].Transport Policy, 2006,13:413-425.

[11] Shrivastava P,Dhingra S L.Development of feeder routes for suburban railway stations using a heuristic approach[J].Journal of Transportation Engineering, 2001,127:334-341.

[12] Shrivastava P,Dhingra S L.Development of coordinated schedules using genetic algorithms[J].Journal of Transportation Engineering,2002,128:89-96.

[13] Ceder A.Public transit planning and operation:theory, modelingand practice[M]. Burlington, MA: Elsevier,2007.

Research on Optimal Routing of Community Shuttle Connect Rail Transit Line

XIONG Jie,GUAN Wei,HUANG Ai-ling
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University,Beijing 100044,China)

Community shuttle plays an important role in the efficient operation of public transit microcirculation.The optimization of community shuttle routes is also an important work to enable community shuttles to connect rail lines well.This paper defines the potential passenger demand indicators from the view of segments in a given network first,then aims at generating a cyclic route with the objective of maximizing the potential passenger demand,considering the maximum travel time constrain and the characteristics of the cyclic routes.In solving the problem,a set of algorithm for crossover and mutation of route segments is presented,by this a genetic algorithm(GA)can be carried out smoothly to solve the problem as a heuristic algorithm.At last,a case study of Tiantongyuan Community in Beijing is presented.GA and a depth first search(DFS)are both presented to work out the optimal shuttle route serviced for the community based on the passenger count data.The results show that the solution obtained by GA is the optimal route in this case, so GA is feasible in solving this kind of problem.

integrated transportation;route optimization;genetic algorithm;community shuttle; connection;transit line

1009-6744(2014)01-0166-08

U121

A

2013-05-30

2013-08-18录用日期:2013-08-29

国家自然科学基金(71131001-2);“973”国家重点基础研究发展计划(2012CB725403-5);北京交通大学优秀博士生科技创新基金资助项目(2013YJS045).

熊杰(1988-),男,黑龙江哈尔滨人,博士生.*通讯作者:weig@bjtu.edu.cn