“变”中找“定”
——浅析平面向量几何法
● (云和中学 浙江云和 323600)
物质世界中的万事万物都处在相互作用的普遍联系之中,都处在不断产生、不断消亡的运动、变化和发展的永恒过程之中,运动是永恒的、静止是相对的,运动和静止之间存在普遍的联系.在数学中也是如此,我们经常会遇到一些变化和运动的问题,而合理的分析和利用变化中的不变性,让“变”与“定”有机地结合起来,对于解决问题往往能起到一针见血的作用.下面结合平面向量几何法的教学实践浅析“变”与“定”之间的对立统一关系.
平面向量丰富了高中数学内容,同时作为工具性知识,可以与很多知识联系.平面向量具有双“二维”性,即本身有方向、大小,运算有代数、几何,大大地提高了学生学习这块知识的能力要求.在高考中大多以选择题和填空题的形式出现,题目灵活、多变,部分题目以能力立意命题,要求学生有一定的数形结合思想和能力.教师在平面向量的课堂教学和复习中经常会用到向量的几何法,渗透数形结合的思想,但学生对于数形结合能力的掌握却不一定到位,“光有思想没有能力”是很多学生在学习平面向量时的困惑.
在平面向量的几何法中,紧扣向量运动变化中的定性,结合定值,合理作图,可以使很多抽象的问题变得直观、具体,易于切中要害,立竿见影.平面向量的几何运算中往往涉及长度、夹角、和、差、数量积、投影等概念和知识点,如能把握上述量中的不变量,就可以轻松地在变化和运动中求解一类定值和最值问题.
1 向量的长度为定值问题
在平面向量的教学中,有这样的问题:把平面内所有的单位向量移到同一起点,则终点构成什么样的图形?答案是单位圆.这类问题中向量的方向任意变化,而长度为定值,可以结合到定点的距离等于定值的点的轨迹为圆,数形结合几何作图,利用圆的性质解决问题.


(2011年浙江省数学高考理科试题)

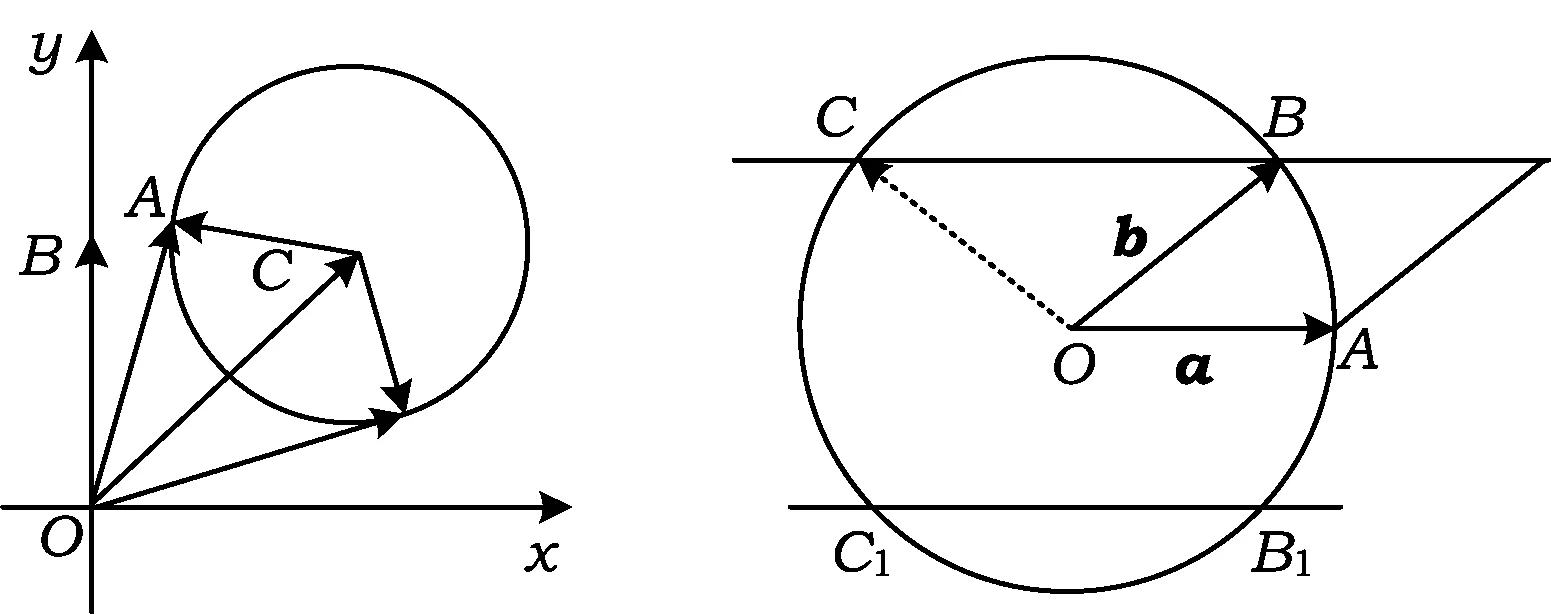
图1 图2
2 2个向量的夹角为定值问题
平面向量的方向一般不单独考查,但2个或多个平面向量放在一起研究时,由于有了参照物,就可以研究2个向量的夹角问题.当2个向量的夹角为定值时,可以结合同弧(弦)所对的圆周角相等作出点的轨迹,数形结合解决问题.
例2(1)已知平面向量α,β(α≠0,α≠β)满足|β|=1,且α与β-α的夹角为120°,则|α|的取值范围是______.
(2010年浙江省数学高考理科试题)

(2011年全国数学高考试题)

故

图3 图4
3 平面向量基本定理和三点共线问题
平面内任意2个非零不共线向量都可以作为一组基底,平面内任意一个向量都可以由这一组基底唯一线性表示,平面向量基本定理中蕴含着基底的思想和意识.特别是在一些数量积运算中,把已知信息最多的2个向量作为一组基底,先将要进行数量积运算的2个向量转换成用基底线性表示,再用基底线性表示结果来进行数量积运算,可以起到以不变应万变的效果.平面向量基本定理的一种特殊情况,当向量的起点相同,基底线性表示的系数和为1时,就有了3个向量的终点在同一直线上的三点共线问题.这类问题要求对线性表示的系数有敏锐的观察力和简单的处理技巧,只要方法到位,就可以将代数运算转换成几何运算,减少不必要的化简过程,较好地从几何角度理解和诠释问题的背景.

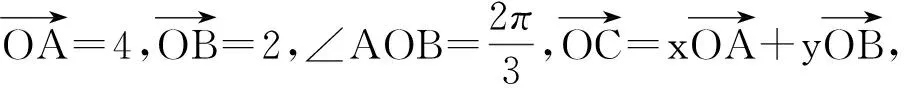
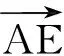



图5 图6


4 向量数量积问题中投影为定值问题
向量的数量积运算包括几何法和坐标法,在几何法中,a·b=|a||b|cos

图7 图8
例4(1)已知a是平面内的单位向量,
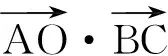
(2012年浙江省数学高考调研试题)
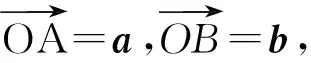

因此









5 数量积运算中2个向量的和或差为定值问题
极化恒等式是泛函分析中的知识,它表示内积可以由它诱导出的范数来表示.极化恒等式在高中平面向量中的简化应用为恒等式
而这个公式可以更加形象地记忆为“积化和差”公式.在平面向量求数量积的问题中,若2个向量都是变量,而2个向量的和或差为定值,可以利用“积化和差”公式减少变量个数或转化成为研究定值问题.

(2012年浙江省数学高考理科试题)

图9 图10

( )
A.∠ABC=90° B.∠BAC=90°
C.AB=ACD.AC=BC
(2013年浙江省数学高考理科试题)


“变”与“定”是对立的,“变”与“定”又是统一的.合理地处理好“变”与“定”之间对立统一的关系,能更深刻地理解数学,更科学地看待变化,更清晰地认识世界.

