例谈椭圆与直线的相切问题——2014年浙江省数学高考理科第21题赏析

● (杭州第十四中学 浙江杭州 310006)

直线与圆锥曲线的综合问题是高中解析几何的一个重点内容，在历年高考中都是区分题的载体，比如2014年浙江省数学高考理科第21题.据了解，这个满分15分的解析几何题，全省平均分5分左右．

2014年浙江省数学高考理科第21题如下：

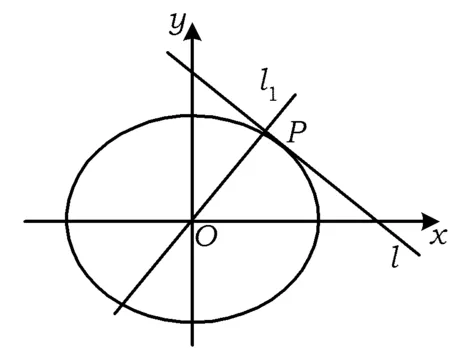
图1

(1)已知直线l的斜率为k，用a,b,k表示点P的坐标；

(2)若过原点O的直线l1与l垂直，证明：点P到直线l1的距离最大值为a-b．

看到此题，笔者的第一感觉是这个题目很常规、很普通，主要考查了直线与椭圆的位置关系、点到直线的距离等基础知识，以及对分式的处理、基本不等式的应用等综合能力．考生经历了3年的高中数学学习，特别是高三的复习，应该具备了应对此类问题的能力．但从考生反映及阅卷情况来看，这个题目的完成情况不那么理想，值得推敲.这里笔者将自己的一些体会记录下来，与大家分享．

1 解决问题——欲善其事，先利其器

1．1 第(1)小题的解决

该小题宽口径，入手方法多，考查学生的分析能力、应变能力，尤其是运算能力，能够起到高考选拔优质生源的作用．

思考角度1直线与椭圆的相切问题，掌握切线方程是首选．

解法1设P(x0,y0)，则过点P的切线方程为

得

(1)

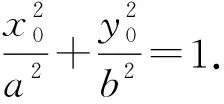
(2)

结合式(1)、式(2)及点P在第一象限，得

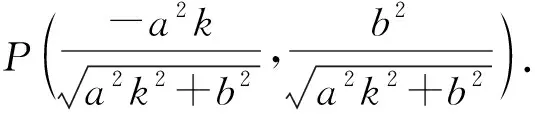
注这里得到斜率后，联立方程(1)和方程(2)，消元求解是关键．

思考角度2结合导数的定义，利用导数来处理相切问题，不失为一条捷径．

以下同解法1．

注这里的求导过程涉及二元函数“隐函数”求导，普通学生未必能够掌握，于是解法3引入2个交点，由“点差法”简化运算，并利用“切线是割线的极限”这一思想来解决问题．

解法3设P(x0,y0)，假设直线l与椭圆C有2个交点，分别记为P1(x1,y1)，P2(x2,y2),由点P1,P2在椭圆C上，得

(3)

(4)

式(3)-式(4),得

(5)

由椭圆切线的几何意义，对式(5)求极限得

从而

以下同解法1．

思考角度3考虑到直线与椭圆相切的代数意义，即联立直线与椭圆的方程组有且只有1组解，故可利用判别式法来求解．

解法4设直线l的方程为

y=kx+m(其中k<0,m>0)，

联立方程组

消去y得

(a2k2+b2)x2+2a2kmx+a2m2-a2b2=0,

从而

Δ=4a4k2m2-4(a2k2+b2)(a2m2-a2b2)=0，

于是

m2=a2k2+b2.

由题意m>0,得

求得

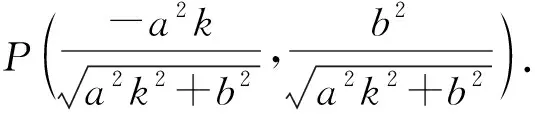
解法5设P(x0,y0),直线l的方程为

y-y0=k(x-x0)，

联立方程组

整理得 (b2+a2k2)x2+2a2(ky0-k2x0)x+

由题意知Δ=0，化简得

(6)

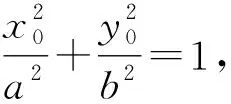
(7)

即

从而

以下同解法1．

注解法4采用直线方程的“斜截式”，解法5采用直线方程的“点斜式”，虽然前者引入新的参数m，但是计算过程较简单；而解法5计算量大，式(7)的变形也不容易想到，作为方法可以介绍给学生，但不值得推荐．

思考角度4相比直线与椭圆相切，直线与圆的相切问题比较容易解决，故考虑通过坐标变换，将椭圆方程变成圆方程来处理．

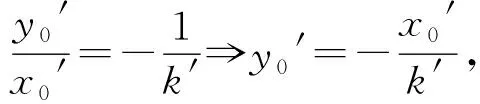
代入x0′2+y0′2=1得

从而

还原为x0,y0坐标，即

由点P在第一象限，且k<0，开方得

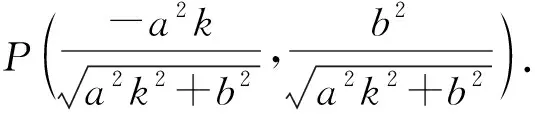
思考角度5考虑椭圆的参数方程，避开解方程的过程，从三角函数的变换性质入手，直接求切点坐标．

解法7设P(x0,y0)，则过点P的切线方程为

(8)

从而

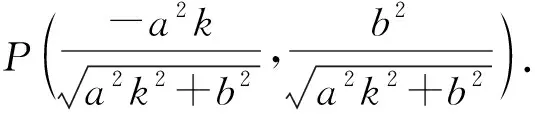
1．2 第(2)小题的解决

该小题从点到直线的距离公式入手，要求学生掌握基本的处理分式的方法，并能灵活应用基本不等式得到最大值．是否具备处理分式的综合能力一直以来都是浙江省高考命题组对理科考生的考查内容[1]，该小题也很好地体现了这点．

2 追溯问题——他山之石可以攻玉

2．1 透过竞赛看高考

2004年全国高中数学联赛四川省初赛第16题：

解设A(x1,y1),B(x2,y2),直线AB的方程为：y=kx+m．因为点A既在椭圆上，又在直线AB上，从而

消元得 (a2k2+b2)x2+2kma2x+a2(m2-b2)=0.

由于直线与椭圆相切，故

Δ=(2kma2)2-4(a2k2+b2)a2(m2-b2)=0,

(9)

同理，由点B既在圆上又在直线AB上，可得

(10)

由式(9)、式(10)得

从而 |AB|2= (1+k2)(x2-x1)2=

2．2 透过其他省份看浙江高考

2013年山东省数学高考理科卷压轴题：

(1)求椭圆C的方程；

(2)点P是椭圆C上除长轴端点外的任一点,联结PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围；

3 教学建议——前事不忘，后事之师

3．1 重视基础

在教学中，首先应落实解析几何的一些基本概念，如直线的倾斜角、斜率、截距、圆锥曲线的长短轴、焦距、离心率、焦半径等.其次应掌握基本公式，如直线方程的各种形式、两点间距离公式、点到直线的距离公式、斜率公式、弦长公式、切线公式等.再者要熟悉处理解析几何问题的基本方法，如求圆锥曲线轨迹方程的方法：定义法、直接法、相关点法、参数法、几何法、待定系数法等；判断直线与圆锥曲线位置关系的方法：判别式法、几何法等．

3．2 强调能力

在解析几何复习过程中，教师除了要教会学生“怎么做”，应更多地着眼于让学生体会到“为什么这么做”．课堂上少一点高高在上的“满堂灌”，多一些接地气的启发式提问．碰到难题，教师要避免“一条龙”地包干到底，应鼓励学生自己找到问题的突破口，并通过繁复的计算解决问题．对于例题、课后习题的选择，也应立足于“精”，而不在于“多”，应鼓励学生一题多解，善于用不同方法解题，培养学生多角度思考问题的能力，提升思维水平，提高数学素养．

参 考 文 献

[1] 夏霖,马茂年．从分式运算对理科学生的解题要求谈起——对浙江省数学高考试题的几点思考[J]．中学教研(数学)，2013(8)：11-12.

[2] 赵似花．多角度思考 全方位突破——2013年山东省数学高考压轴题的解法探究[J]．中学教研(数学)，2013(8)：42-45.