研究教材 用好教材——以“椭圆的概念及标准方程”课为例

● (菱湖中学 浙江湖州 313018) ● (杭州第四中学 浙江杭州 310018)

1 问题的提出

随着新一轮课程改革的深入，“不是教教材，而是用教材教”的教材使用观越来越得到广大一线教师的认同和研究．但是在实际的课堂教学中，也有部分教师没有真正理解“不是教教材，而是用教材教”的内涵，从而出现了片面脱离教材进行课堂教学的情形，甚至在部分教师的课堂上，学生从头至尾都没有翻阅教材．

笔者近日听了几堂椭圆概念的新授课，也看了几篇“椭圆的标准方程”同课异构课的教学设计，都给人一种意犹未尽之感．

遗憾1由于时间太仓促，一节完整的椭圆概念课，被分成了2天2节课来实施教学，知识点之间失去了连贯性．大部分任课教师为了一节课的完整性，都掐掉了从圆到椭圆的演变过程，没有考虑学生对椭圆第一认识的感官知觉，对课前的引入素材没有作事后的论证．

遗憾2没有很好地使用课本提供的素材，比如本节开头提供的动手操作探究部分；更没有对课本素材进行深挖掘，比如课本提供的例2；课后的探究与发现部分，也没有为后续知识的教学提供相适应的铺垫．

由于以上原因，笔者做了一次尝试，通过换课，一天内2节课连上，使课堂有了充足的时间保证，并对“椭圆的标准方程”作了再设计，将其定义为“椭圆的概念及标准方程”．

2 教学再设计

2.1 情景引入

师(拿起预先准备的圆柱形玻璃水杯)：同学们，请看杯子里的水面是什么形状的？

生(众)：圆形．

教师把杯子稍作倾斜，再次问：现在的水面又是什么形状呢？

生(众)：椭圆．

师：很好！的确是一个椭圆．是否可以说圆柱的斜截面是一个椭圆呢？椭圆和圆之间又有什么联系呢？

生1(稍作思考后)：圆柱的斜截面是一个椭圆，而且，由刚才玻璃杯水面形状的变化特点，我认为椭圆可以由圆经过拉伸或压缩而得到．

2.2 概念的形成与概括

(以下是对教材探究部分的教学.)

师：不错，椭圆的确可以由圆经过不同程度的拉伸或压缩而得到．那么，什么是椭圆呢？总要给椭圆一个属于自己的定义，并给出椭圆的方程形式．这节课我们就来学习“椭圆的概念及标准方程”．

师：下面请同学们拿出昨天要大家准备的细绳、厚一点的硬纸板、2颗图钉，将细绳的2端用1个图钉固定在纸板的同一点处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖(动点)画出的轨迹是什么？

生(一齐)：是一个圆．

师：能解释一下以上作图中的几何原理吗？

生：平面上到一个定点(图钉)的距离等于定长(绳子折叠后的长)的点(笔尖)的轨迹为圆．

师：下面，我们再画一次，将细绳的2端拉开一段距离，分别用图钉固定在纸板的2个点处，套上铅笔，拉紧绳子，移动笔尖，画出的轨迹又是什么曲线？

评注从2个点重合到2个点分开，在实际操作中，体验从圆到椭圆的演变过程．

学生(一齐)：是一(半)个椭圆．

师：的确是一个椭圆，得到半个椭圆的同学是少画了2个图钉的下方部分或上方部分．那么，谁能说出，在这次画图过程中，移动的笔尖(动点)所满足的几何条件？

生2(稍作思考)：由于在笔尖移动的过程中，绳子的长度保持不变，2个图钉可以看成2个定点，因此笔尖满足的几何条件是：笔尖(动点)到2个定点(图钉)的距离等于定长(绳子的长度)，另外，由于绳子在2个图钉间的部分是宽松的，因此，这个定长大于2个定点之间的距离．

师：非常好，生2其实已经道出了椭圆的定义：我们把平面内与2个定点F1,F2的距离和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．这2个定点叫做椭圆的焦点，2个焦点间的距离叫做椭圆的焦距．

图1

师：请同学们参看图1，并结合椭圆定义，对照椭圆定义的文字语言和图形语言，试着将其转化为符号语言．

生3：设M是椭圆上的任意一点，则椭圆可以表示成以下点的集合：

{M||MF1|+|MF2|=2a，2a为大于|F1F2|的常数}．

师：非常不错，现在我们有了椭圆的文字定义、图形与符号定义，有了这些，我们就可以解决为什么圆柱的斜截面是椭圆的问题.下面，请同学们翻到课本第42页，仔细阅读“探究与发现——为什么截口曲线是椭圆”，并试着解决“为什么圆柱的斜截面是椭圆的问题”．

很快，不少学生仿照证明圆锥的斜截面是椭圆的方法证明了“圆柱的斜截面是椭圆”．

评注与课堂引入相呼应，解决了茶杯倾斜后的水平面是椭圆的问题，并加深了学生对椭圆定义的理解．

2.3 椭圆标准方程的推导

通过研究曲线的图形和方程可以得到它的各种性质，也就是所谓的“数形结合”．下面，我们根据椭圆定义的文字表示和符号表示，并结合图形特点，来推导它的方程．

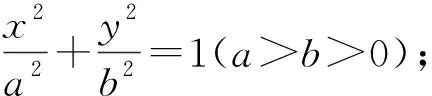
评注这一过程与大多数任课教师的设计相差不大，笔者不再赘述．

2.4 例题设计，深化概念

通过例题设计，加深学生对椭圆标准方程的把握和椭圆定义的理解．

例1判断下列椭圆的焦点在哪个轴上，并写出焦点坐标：

例2分别求适合下列条件的椭圆的标准方程：

(1)a=4，b=3；

(2)焦点F1(0,-3),F2(0,3)，a=5；

(4)经过点A(-7,0),B(0,4)．

评注通过例1及例2，特别是例2的第(1)小题，使学生能正确区分或考虑焦点在x轴或y轴上2种情形，并解决a2,b2与a,b容易相混淆的问题；通过例2第(3)小题的2种解法，向学生渗透待定系数法(解方程思想)与定义思想的运用；通过例2第(4)小题的教学，向学生渗透数形结合思想与待定系数法(解方程思想)．

2.5 与引入呼应，再次探究

例3如图2，在圆x2+y2=a2(a>0)上任取一点P，过点P作x轴的垂线PD，当点P在圆上运动时，线段PD中点M的轨迹方程是什么？

图2

解设点M(x,y)，点P(x0,y0)，则

因为点P(x0,y0)在圆x2+y2=a2上，所以

x2+4y2=a2，

即

因此点M的轨迹是一个椭圆．

评注此例题以教材中的例2为蓝本进行改编，增强了知识的一般性与探究的连续性．

师：通过这道例题，我们是否能从点的角度，并以代数为媒介，剖析圆与椭圆的关系？

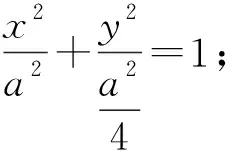
师：非常不错！生4向我们解释了从圆到椭圆的演变过程．谁能结合例3的方法再次解释一下为什么“茶杯倾斜后的水平面是椭圆”的问题．

图3

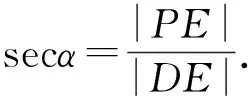
师：很好！生5从代数方程的角度说明了为什么茶杯倾斜后的水平面是椭圆．

2.6 设计操作串，构建圆到椭圆的演变链

师：前面我们知道了什么是椭圆、椭圆的标准方程及椭圆与圆的关系．下面请同学们再次动手，拿出细绳、厚一点的硬纸板、2颗图钉，将细绳的2个端分别用一个图钉固定在纸板的2个点处，套上铅笔，拉紧绳子，移动笔尖，画出椭圆；接下去，再将2颗图钉沿着2颗图钉确定的直线向外平移相同的距离，再次画出椭圆；如此多重复几次，观察随着图钉的外移，椭圆发生了什么变化．

生：椭圆越来越扁．

师：我们用离心率e来表示椭圆的宽扁程度，既然称为离心“率”，那肯定是一个比值．从刚才2颗图钉从重合到分离，到距离越来越大，导致图形由圆变化到椭圆，再慢慢变扁的过程，我们可以用哪2个量的比值来表示离心“率”呢？

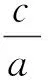
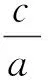
评析将此部分内容提前，建立从圆到椭圆变化的完整知识体系．

3 结语

调研表明，出现脱离课本进行教学的原因主要有以下几个方面：

第一，许多教师认为教材内容太“简单”，不足以应付高考．诚然，教材的“基础性”与高考的“选拔性”的确有一定的目标差异，但学好教材一定是高考取得好成绩的前提，教师的主要精力应当放在帮助学生熟练掌握教材内容上．

第二，由于目前现成的教辅资料、学案、课件、教案比比皆是，教学中拿来主义的现象比较严重，导致许多教师不善于或不愿意花大力气研究教材．

第三，误解课改提倡的“不是教教材，而是用教材教”，要“创造性地使用教材”的真正意图．我们要创造性地使用教材，但创造性地使用教材不是脱离教材．毕竟教材的结构体系、内容顺序是专家反复考量的，语言是字斟句酌的，例题是反复打磨的，习题是精挑细选的．因此，在教学中，要仔细分析教材的编写意图，将教材的编写思想渗入我们的课堂教学中．在处理教材时，内容的调整、顺序的调整要十分小心(否则容易导致教学目标的偏离)，要根据知识结构的特点和学生的实际认知而行，案例和例题可以根据学生基础和当地教学环境替换，但所换的案例和例题要反映教科书的编写意图，要能承载教材中案例和例题的教学任务．

教之道在于“度”，学之道在于“悟”．在课堂教学中，我们要不断地研究教材，研究教材的编写意图，创造性地使用教材，才能很好地把握教材使用的“度”．