“定论问题”的类型与求解策略

● (海门中学初中部 江苏海门 226100)

在近几年各地的数学中考中，常常出现这样一类问题：某些代数式、函数式、方程、坐标或几何问题等，无论其中的字母或待定系数如何取值、图形位置如何变化、动点如何运动等，问题始终保持原有的性质、结论不变(即问题的性质、结论与字母或待定系数的取值、图形位置变化无关)，不妨称之为“定论问题”.本文以中考试题为例，对其类型与求解策略作一阐述.

1 “定论问题”的类型

“定论问题”一般有：求代数式的值、特定条件下待定系数的值(范围亦或系数间关系式)、定点坐标、定直线解析式、特设条件下的一般函数解析式；证明图像恒过定点、点恒在定直线上；判断数学概念是非问题；探究说明某几何量为定值、图形恒有某确定的位置关系、某特定的性质等类型.

2 “定论问题”求解策略

2.1 利用主元与无关思想

把多元代数式按某个字母(即取值与之无关的字母)为主元整理，按无关思想令主元的各系数为0，求出待定系数的值，则问题获解.

例1若代数式(x2+ax-2y+5)-(bx2-2x+6y-1)的值与字母x的取值无关，求(a+b)2 013的值．

分析这是确定系数值,进而求代数式值的问题.把原式化简整理为以x为主元的代数式,得

原式=(1-b)x2+(a+2)x-8y+6.

因为原式取值与x无关，所以上式中不含x，从而

1-b=0且a+2=0，

解得

a=-2，b=1，

故

(a+b)2 013=-1．

2.2 配方

通过配方，以其“以偏概全”包罗取值的任意性、无限性之功能，结合非负数的性质使定论问题获解.

例2已知二次函数y=x2+ax+a-2.

(1)证明：不论a取何值，抛物线y=x2+ax+a-2的顶点Q总在x轴的下方；

(2)略.

(2002年浙江省杭州市数学中考试题)

分析证明抛物线顶点的纵坐标为负即可．易得抛物线的顶点为

其纵坐标配方得

因此，不论a取何值，抛物线的顶点总在x轴的下方．

说明本题还可以用下面所述的“方程理论”求解(因为抛物线开口向上，所以只需结合配方法证明判别式Δ>0即可).

2.3 取特殊值

通过取特殊值(虽具有任意性,但一般取简单且易于求解的值)推理运算，根据“一般与特殊”的关系化抽象为具体、化繁杂为简单，从而使定论问题获解.

例3无论a取什么实数，点P(a-1,2a-3)都在直线l上，点Q(m，n)是直线l上的点，则(2m-n+3)2的值等于______.

(2012年江苏省南通市数学中考试题)

分析这是求值类问题.既然点P在直线l上，与a取值无关，不妨取a=0,得P1(-1，-3)；取a=1,得P2(0，-1).由此得直线l的解析式为

y=2x-1.

因为Q(m,n)在直线l上，所以

2m-n=1，

故

(2m-n+3)2=16.

说明本例还可用主元与无关思想及下面所述的消元法、方程理论、多项式相等理论求解.

2.4 消元

构造联立函数式，通过消元确定定论问题所求的解析式.消元法对于求定直线等函数式类定论问题十分简捷.

例4抛物线y=ax2+2x+3(a≠0)对任意实数a，其顶点都在某直线l上,求直线l的解析式.

(2003年山东省济南市数学中考试题)

说明本例也可以用特殊值法求解，但没有消元法简捷.

2.5 利用方程理论

(1)关于x的一元一次方程ax=b有无数个解⟺a=b=0.

(2)关于x的一元二次方程ax2+bx+c=0(或二次函数y=ax2+bx+c，其中a≠0)有2个不相等的实数根(或二次函数与x轴有2个交点)⟺Δ>0；有2个相等的实数根(或二次函数与x轴有且只有1个交点)⟺Δ=0；没有实数根(或二次函数与x轴没有交点)⟺Δ<0.

运用上述方程理论求解某些定论问题十分便利，但运用一元二次方程判别式时常常需要用到配方法，并结合非负数的性质.

例5使函数值为0的自变量的值称为函数的零点．己知函数y=x2-2mx-2(m+3)(m为常数).

(1)略；

(2)证明：无论m取何值，该函数总有2个零点．

(2011年湖南省长沙市数学中考试题)

分析函数总有2个零点即方程x2-2mx-2(m+3)=0总有2个不相等的实数根，把判别式配方得Δ=4(m+1)2+20>0,由方程理论(2)知，无论m取何值,函数y=x2-2mx-2(m+3)总有2个零点．

2.6 利用多项式理论

有些定论问题可以运用这2个多项式相等理论来求解.关于x的多项式：

(1)anxn+an-1xn-1+…+a1x+a0=0⟺an=an-1=…=a1=a0=0；

(2)anxn+an-1xn-1+…+a1x+a0=bnxn+bn-1xn-1+…+b1x+b0⟺an=bn，an-1=bn-1，…，a1=b1，a0=b0.

例6对于二次函数y=x2-3x+2和一次函数y=-2x+4，把y=t(x2-3x+2)+(1-t)(-2x+4)(t≠0)称为这2个函数的“再生二次函数”，其图像记作抛物线E．

(1)略.

(2)二次函数y=-3x2+5x+2是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，请说明理由．

(2012年江苏省镇江市数学中考试题)

分析这是探索概念是非的问题.函数

y=t(x2-3x+2)+(1-t)(-2x+4)

可化为

y=tx2-(t+2)x-2t+4.

若y=-3x2+5x+2是“再生二次函数”，则

tx2-(t+2)x-2t+4=-3x2+5x+2.

根据多项式相等理论,得

t=-3,-(t+2)=5,-2t+4=2

应同时成立,显然这是不可能的.故y=-3x2+5x+2不是“再生二次函数”.

2.7 利用函数性质

有些定论问题可以运用这些函数性质来求解.

(1)对于函数y=ax2+bx+c(或代数式ax2+bx+c，其中a≠0):

①若a>0,Δ<0,则y>0(或ax2+bx+c>0)；

②若a<0,Δ<0,则y<0(或ax2+bx+c<0).

(2)若2个函数y1,y2的图像有2个交点、1个交点、0个交点，则这2个函数式联立组成的方程组有2个解、1个解、没有解，即消元后所得的一元二次方程的判别式Δ>0，Δ=0，Δ<0，反之亦然.

例7a,b,c为三角形的3条边长，证明：不论x为何实数，总有b2x2+(b2+c2-a2)x+c2>0.

证明因为b2>0，且

Δ= (b2+c2-a2)2-4b2c2=

(b2+c2-a2+2bc)(b2+c2-a2-2bc)=

(b+c+a)(b+c-a)(b-c+a)(b-c-a)<0,

由函数性质(1),得

b2x2+(b2+c2-a2)x+c2>0.

2.8 运用几何原理

几何定论问题一般运用几何原理来求解.

图1

例8如图1，⊙O的直径AB=2,射线AM,BN为半圆的切线，在AM上取一点D，联结BD交半圆于点C，联结AC．过点O作OE⊥BC于点E，交BN于点F；过点D作DP切半圆O于点P，交BN于点Q．

(1)(2)略；

(3)求证：当点D在AM上移动时(点A除外)，点Q始终是线段BF的中点．

(2011年山东省潍坊市数学中考试题)

分析这是几何定论问题.易得△ABD∽△BFO，从而

于是AD·BF=2.

(1)

由切线长定理,得

DA=DP，QB=QP.

过点Q作QK⊥AM于点K，在Rt△DQK中，

DQ2=KQ2+DK2，

即

(AD+BQ)2=22+(AD-BQ)2,

得AD·BQ=1.

(2)

由式(1)和式(2)，得

BF=2BQ，

故点Q为BF的中点．

2.9 综合法

有的定论问题需要综合运用多种方法求解才能奏效.

分析抛物线解析式可化为关于a的方程

2(2x+1)a=4y-4x2-4x-1.

因为a可任意取值，即方程有无数个解，所以

于是

消去a，得所求抛物线的解析式为

说明本题运用了方程理论(1)、消元法，当然求定点也可用主元与无关思想、特殊值法等.

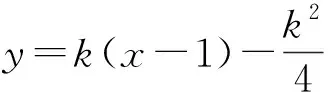
(2012年广西壮族自治区南宁市数学中考试题)

分析这是求值(进一步确定函数解析式)问题.联立2个函数，消去y，整理得

4ax2+4(b-k)x+k2+4k+4=0.

因为2个函数图像对任意的实数k都只有1个公共点，所以由函数性质(2)得上述方程的判别式Δ=0，即

(1-a)k2-2(2a+b)k+b2-4a=0.

由于此式对任意的实数k都成立，根据主元与无关思想或多项式相等理论有

1-a=0，2a+b=0，b2-4a=0，

故a=1，b=-2(函数解析式为y=x2-2x+1)．

说明本题运用了主元法、函数性质、多项式相等理论等.

求解定论问题要通过相应策略在变中寻不变，化动态为静态，抓住不变情形应对.需要指出的是，同一题目有时有多种策略求解(如例3有5种策略)，有的题目又需要综合运用多种策略协同作用才能奏效.因此，具体解题时要针对题型选用最优的方法应对.