例说2道概率题目的深层剖析

● (玉门市第一中学 甘肃玉门 735211)

自2010年甘肃省实施新课程以来,“条件概率”便进入了高中数学.4年来,大部分数学教师已讲授过该内容,也有一部分教师初次学习并讲授“条件概率”等内容.面对新的问题,因缺少经验,在教学过程中他们像学生一样容易犯种种错误.为了有效应对在“条件概率”教学中发生的各种困局,下文举2个例子深度剖析原因,以飨读者.

1 高考题目参考答案中的“·”

在高三集体备课会上,一个偶然的机会,教师1提出了2012年安徽省数学高考理科试题第17题的参考答案是错误的.同时,他对参考答案进行了错误分析,并给出了自己的解法.

1.1 题目及参考答案

例1某单位招聘面试,每次从试题库随机调用一道试题,若调用的是A类型试题,则使用后,该试题回库,并增补一道A类试题和一道B类型试题入库,此次调题工作结束;若调用的是B类型试题,则使用后该试题回库,此次调题工作结束.试题库中现共有m+n道试题,其中有n道A类型试题和m道B类型试题,以X表示2次调题工作完成后,试题库中A类试题的数量.

(1)求X=n+2的概率;

(2)(略).

解(1)记“第i次调题调用到A类试题”为事件Ai(i=1,2)，则

1.2 教师1对参考答案的分析及提供的解法

接着,教师1提供了自己的答案如下:

将调题工作按首次是否调用A类试题分为2类:(1)若首次调用A类试题,则第1次调题有n种方法,第2次调用试题有m+n+2种方法;(2)若首次调用B类试题,则第1次调题有m种方法,第2次调用试题有m+n种方法,故2次调题工作,共有n(m+n+2)+n(m+n)种方法.当X=n+2时,调题方法数为n(n+1),依古典概率模型有

P(X=n+2)=P(A1A2)=

由上可知,高考试题所提供的答案是错误的,原因是将X=n+2时的概率错误地认为P(A1)·P(A2),忽视了判断事件A1与事件A2的相互独立性(只有当2个事件相互独立且都发生时,计算概率才用“·”).

1.3 对以上2种解法的深层剖析

初看教师1对参考答案的分析与提供的解答,合情合理,天衣无缝,令全体教师有口难辩.顿时,时间像停止了一样,但大家觉得高考答案不可能有误,那问题出在哪里呢?会后,经笔者仔细分析,过程如下：

先讨论教师1提供的“答案”,他将调题工作分为2类,首次调用A类试题和首次调用B类试题.依分类加法计数原理共有n(m+n+2)+n(m+n)种方法,而满足X=n+2的方法有n(n+1)种,由古典概率模型可得

在该过程中利用了“分类加法计数原理”与“古典概率模型”这2个概念,为了清楚无误地解说过程,我们从概念出发,从中剖析问题的根源.

分类加法计数原理完成一件事有2种不同方案：在第1种方案中有m种不同的方法;在第2种方案中有n种不同的方法,那么完成这件事共有m+n种不同的方法(2种不同方案中的方法数互不相同).

古典概率模型我们将具有以下2个特点的概率模型称为古典概率模型：

(1)试验中所有可能出现的基本事件只有有限个;

(2)每个基本事件出现的可能性相等.

对于分类加法计数原理,该教师做到了2种不同方案中的方法数互不相同,对于古典概率模型的特点(1)不言而喻.而对特点(2),本题共有n(m+n+2)+n(m+n)个基本事件,每个结果发生的可能性是否相同呢?经仔细研究,举例如下:

记“第1次调用A类试题”为事件A1,“第2次调用A类试题”为事件A2,“第1次调用B类试题”为事件B1,“第2次调用B类试题”为事件B2,因为事件A1与事件A2,事件B1与事件B2为条件关系,所以

P(A1A2)=P(A1)P(A2|A1)=

P(B1B2)=P(B1)P(B2|B1)=

由此可见,P(A1A2)≠P(B1B2),因此首次调用A类试题和首次调用B类试题所对的基本事件发生的可能性不相等,不满足古典概率模型的基本概念.

再讨论教师1对“参考答案”的分析,在参考答案中事件A1与事件A2不相互独立,故P(A1A2)≠P(B1B2)成立,而事件A2是事件A1发生的条件下发生的,于是利用条件概率公式有

成立.

教师1没有认识到条件概率公式,误以为是使用公式

通过以上分析，对于“·”的使用,我们有了更清楚的认识：当事件A,B相互独立时,

P(AB)=P(A)·P(B);

当事件A发生的条件下,事件B发生时,

P(AB)=P(A)·P(B|A).

2 课本例题解答过程中的“10”与“9”

同样,在集体备课会上,教师2提到人教A版《数学选修2-3》第53页：例2中的第(1)小题解答中“10”与“9”可能写反了.大家随即展开讨论,现将过程整理如下：

2.1 例2及解

例2一张储蓄卡的密码共有6位数字,每位数字都可以从0～9中任选1个,某人在银行自动提款机上取钱时,忘记了密码的最后1位数字,求:

(1)任意按最后一位数字,不超过2次就按对的概率;

(2)略.

2.2 教师2对例2的解的分析及质疑

2.3 对以上质疑的深层剖析

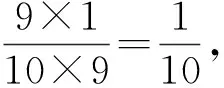
3 感悟

面对新增加的知识要提前做好培训工作.2011年和2012年暑假教育部组织专家轮流对甘肃省教师进行了新课程培训工作,在教育教学理念等方面得到不断提升,但在具体知识的细节方面,没能得到细致指导.作为学校单位,虽然在教研组集体研究学习,也未能预防该类问题的发生.

当然,在平时的教学过程中,应提倡勤钻细研,在面子前讲真理.本文例子中2位教师都从大家不起眼的细节出发,通过努力推敲,面子前讲真理,敢于发表所想,才能给予大家研讨的机会,在研讨中理解知识,形成、建立和交流数学知识,相互学习,共同提升,改进做法,才能提高教学成绩.

最简单的基本思考,最原始的错误理解,也许是每个人学习过程中都需经历的,只要我们善于思考,从问题的概念、原理等出发遵守规则进行推理,搜集文本,挖掘资源,捕捉课堂中鲜活的事例,由点到面,由此及彼,丰富课堂教学内容,提升课堂厚度.唯此,才能使自己的专业得到快速成长.