核截面不确定性引起的keff不确定度的直接蒙特卡罗方法计算

王新哲，喻 宏，王文明，胡 赟，杨晓燕

(1.中国原子能科学研究院 快堆研究设计所，北京 102413；2.中国原子能科学研究院 核物理研究所，北京 102413)

核装置的有效增殖因数keff在核装置设计中起至关重要的作用，其准确度直接影响核装置设计的精度，keff计算的不确定度主要源于以下3个方面：1) 数据的不确定性，包括核数据、装置尺寸以及装载量等数据的不确定度造成的不确定性；2) 计算模型建立中的简化、近似造成的不确定性；3) 计算方法与计算过程中的简化、近似造成的不确定性。随着计算机硬件及计算方法的不断发展，模型建立及计算方法导致keff的不确定度越来越小，影响核装置keff不确定度的重要因素在于数据的不确定性，这其中又以核截面数据的不确定度为主。

现阶段确定核截面数据不确定性对核装置keff计算不确定度的影响的方法主要为灵敏度-不确定度分析方法(S-U方法)[1]，该方法的主要思想是：首先通过直接微扰或共轭方法(广义微扰)确定核装置keff对各核素各截面数据的灵敏度，然后再与协方差矩阵进行数学处理，即可得到核截面数据不确定性造成的装置keff计算不确定度。该方法对于一、二维情况，具有计算速度快并可计算各种核素各截面灵敏度与不确定度的优点，同时，能进行不确定度来源分析，为改善核数据指明方向。但对于三维情况，该方法需用输运或蒙特卡罗方法计算通量的价值函数，在现阶段仍存在计算时间长、计算精度差、计算较繁琐等问题。本文利用直接蒙特卡罗方法计算核截面数据不确定性对核装置keff计算不确定度的影响，以能在现有计算平台上简单、有效地给出keff计算不确定度结果。

1 理论分析

蒙特卡罗方法的主要思想是当所求问题的解是某事件的概率，或某随机变量的数学期望，或与概率、数学期望有关的量时，通过某种试验的方法，得出该事件发生的频率，或该随机变量若干个具体观察值的算术平均值，通过它得到问题的解[2]。

直接蒙特卡罗不确定分析方法在反应堆物理领域，由于计算条件及各种核数据不确定度之间的强相关性等原因，尚未采用。

核装置keff计算中使用的核截面数据，主要由实验测量得到及对测量数据进行数学加工得到。这两种过程中，均会产生一定的不确定度。同时，由于实验测量中的系统误差等因素，各核数据的不确定度相互关联。在评价核数据库中，用协方差数据的形式来描述核数据的不确定度及其相互关联程度[3]。

直接蒙特卡罗方法求解核截面数据不确定性对核装置keff影响的基本思路为：1) 产生1组符合所给截面及相应协方差数据的随机截面数据；2) 运用该组核截面数据通过堆芯计算程序进行keff计算，并记录keff；3) 重复上述两步，直到达到要求的模拟次数；4) 对keff进行统计，得出该组数据的期望值及标准差，所得结果即为keff因核截面数据不确定性导致的不确定度。计算流程如图1所示。

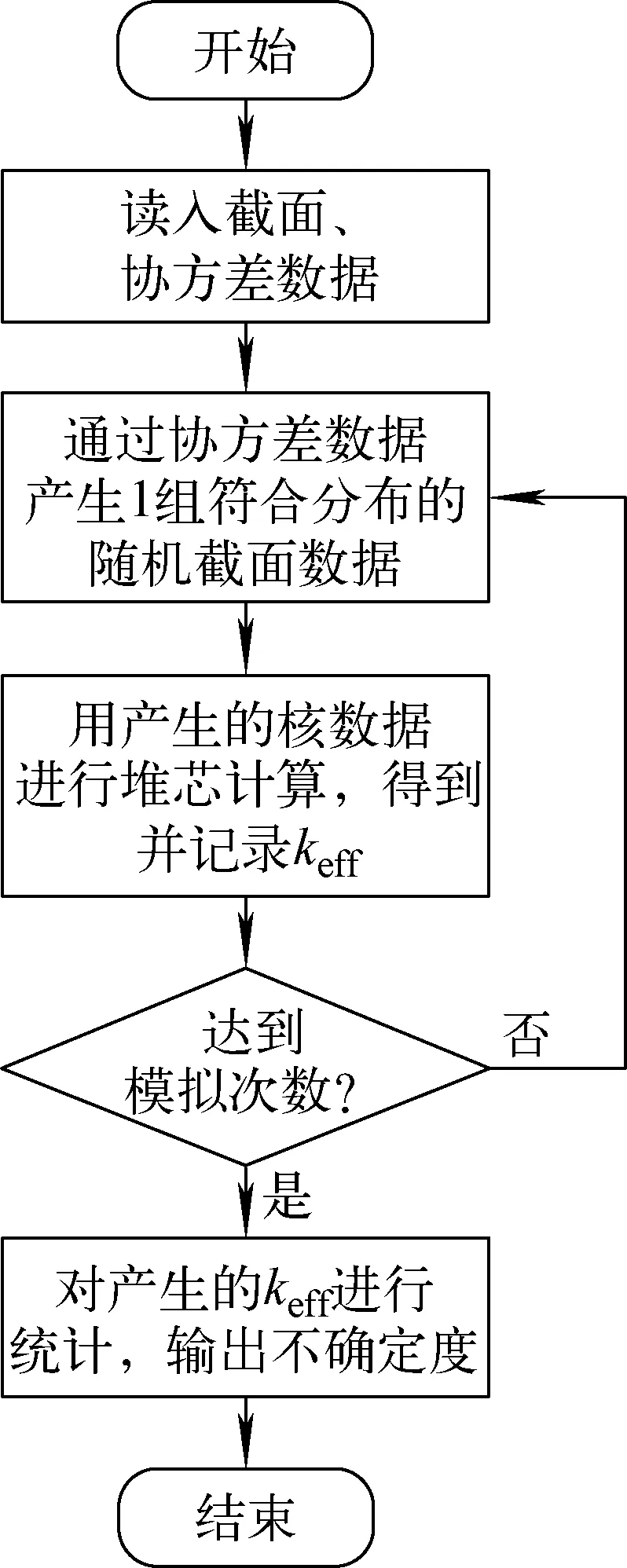
图1 直接蒙特卡罗方法流程图

1.1 随机截面数据产生

从计算流程可知，随机截面数据的产生是直接蒙特卡罗方法中最关键的一步。本文计算过程中假定截面数据的分布符合正态分布，这就要求产生的截面数据既要各自满足正态分布标准，同时又要符合协方差数据要求。由于数据限制，本文仅使用各反应道自身群截面协方差数据，但只要能获得相关数据，即可很容易地扩展到不同反应道之间的计算。

产生n群随机截面数据，首先要求产生n维相互无关符合标准正态分布的随机向量，该随机向量可通过Box-Muller方法[4]由式(1)两两产生：

(1)

其中：U1、U2为在[0，1]上符合均匀分布的随机数；X1、X2为符合(0，1)分布的正态相互无关随机数，通过上述方法，即可产生n维相互无关正态向量X，X～(0，I)(X符合(0，I)分布，其中，I为n维单位矩阵)。

由正态变量的线性变换不变性，即n维随机向量X～(a，B)，若B为n维正定矩阵，C为m×n阶矩阵，且行向量线性无关，则m维随机向量Y=CX～(Ca,CBCT)，其中，CT表示矩阵C的转置[5]。利用该条性质，可将X～(0，I)变换成符合要求的随机向量Y～(sig，C)，sig为核数据中的截面向量。

由于假设核截面数据符合n维随机正态分布，故其协方差阵C对称正定[6]，对于对称正定阵，可通过Cholesky分解得到一个下三角与一个上三角且互为转置的两个矩阵的乘积[7]，如式(2)所示，其中，D为上三角矩阵。

C=DTD

(2)

则对X～(0，I)，有：

DX～(DT0,DTID)～(0,C)

(3)

对DX向量进行平移，即得：

Y=sig+DX～(sig,C)

(4)

其中，sig为未经抽样原始截面数据。通过上述过程，即可产生符合Y～(sig，C)的随机截面数据。

1.2 计算结果分析

本文采用的堆芯计算程序为基于有限差分方法的CITATION程序[8]和基于粗网格节块扩散方法的NAS程序[9]，其基本计算原理均源自多群扩散方程，故只需讨论扩散方程中计算结果的分布即可。算符形式多群扩散方程为：

(5)

其中：M为消失项算符；F为产生项算符；Σf、ΣR分别为宏观裂变截面和宏观移出截面；χ为裂变中子谱；ν为有效裂变中子数。对于核截面数据引起的不确定度分析，可假定除截面外其他各量均为常量，同时截面向量符合正态分布。对于算符F，其中每项均符合正态分布，则由正态向量运算法则可知，FΦ为正态随机向量。对于算符M，除泄漏项外各项皆符合正态分布，泄漏项经过差分后变成扩散系数D的线性运算，因此只需讨论D的分布即可。

按照扩散理论，D的分量Dg为：

(6)

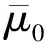
(7)

Dg的分布为倒数正态分布，当μ≥σ时，Dg近似符合正态分布。在核数据尤其是少群核数据中，该假设成立，则：

(8)

其中，X、Y均为多维正态列向量。此时，式(4)可改写为：

kX=Y

(9)

由扩散方程物理意义可知，X、Y中各元素均大于0，故一定存在各项皆为正数的行向量x-1，使得：

x-1X=1

(10)

将式(9)等号两边均乘x-1，即可得：

k=x-1Y

(11)

则由正态变量的线性变换不变性，可得：

(12)

因此，可证得k近似符合正态分布。将程序所得的结果进行正态拟合，可得到数学期望和标准差，所得标准差数据即为核截面数据不确定性导致的核装置keff不确定度。

2 程序开发

(13)

3 算法验证及结果分析

本文分别采用小型核装置Jezebel-239Pu和中国实验快堆(CEFR)首炉装料作为算法验证模型。

3.1 Jezebel-239Pu装置验证

Jezebel-239Pu[10]为239Pu裸球基准装置，半径为6.384 93 cm，基准实验的keff为1.000±0.002，装置核素种类及核子密度列于表1。

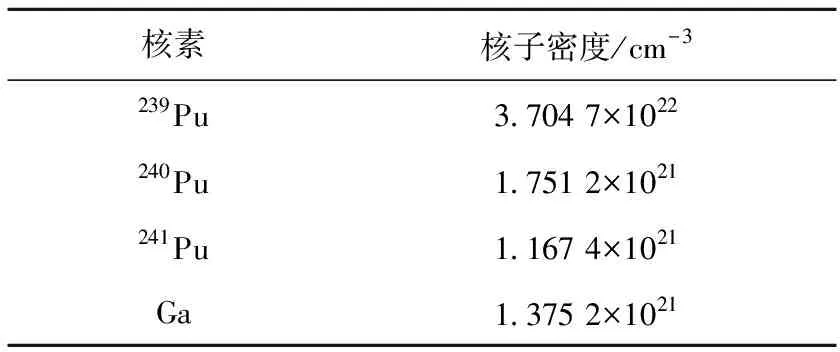
表1 Jezebel-239Pu装置核子密度

因NAS系统基于六角形粗网格节块法，无法用于球形装置计算，故在Jezebel-239Pu计算中只使用CITATION程序。计算中截面数据采用33群截面库及相应的协方差数据，经PASC程序[11]计算共振自屏处理后，得到适合CITATION的输入格式。

对于Jezebel-239Pu这种小型裸球基准装置，因CITATION基于扩散理论，故keff计算值偏小，利用该套多群截面数据计算得到keff=0.955 2。对239Pu的辐射俘获截面σ(n,γ)、σf、σtr进行不确定性分析，所得keff分布及正态拟合结果示于图2。由图2可见，计算结果与正态分布曲线拟合较好。计算结果的统计列于表2(计算条件为Windows7x64，IVF2011，Intel Core i7-2600，所用程序皆为串行程序)，表2同时列出了利用S-U方法[12]所得的不确定数据作为对比，表中统计keff为10 000次计算结果的平均值。

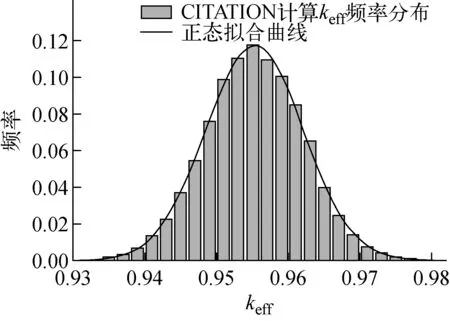
图2 CITATION计算Jezebel-239Pu装置keff分布

分析keff计算不确定度结果可知，该方法结果与S-U方法的差别在20%以内，差别是因为计算所用截面与协方差数据不同，且S-U方法总不确定度计算中考虑了其他一些因素引起的不确定度，如各反应道之间以及裂变中子数引入的不确定度，因此所得结果较本方法的偏大。同时，在进行10 000次计算条件下，程序所需时间小于7 min，时间效率较高。该方法进行1个截面抽样与进行3个截面抽样所用时间一致，因此该方法计算时间主要消耗在堆芯计算程序上，截面抽样带来的额外计算量很小。可看到，在95%置信区间下，不确定度范围很小，所得结果的精度完全满足要求。

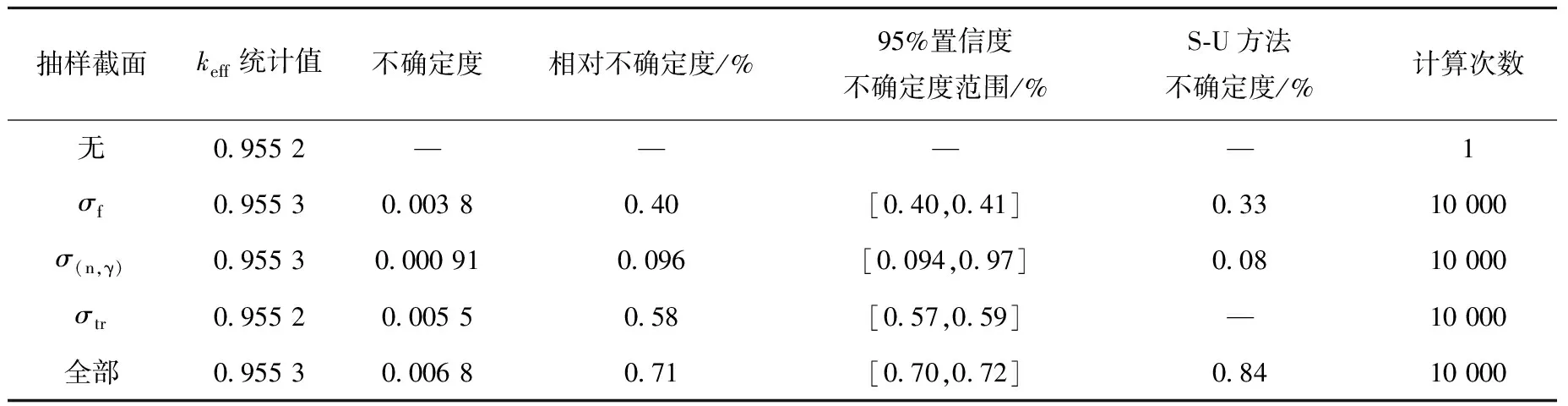
表2 Jezebel-239Pu装置keff不确定度

3.2 中国实验快堆首炉堆芯验证

中国实验快堆首炉堆芯[13]采用富集度64.4%的UO2陶瓷体作为燃料，冷却剂为液态金属钠，包壳材料为不锈钢，堆芯装载示于图3。

图3 CEFR初始堆芯装载布置

计算中采用的协方差数据为中国核数据中心为CEFR制作的6群截面数据，本文对235U与238U的(n,f)、(n,γ)截面以及56Fe和23Na的(n,γ)截面进行抽样，由于现有数据中无238U的截面协方差数据，故采用与235U相同的相对协方差数据作为近似。

计算中截面采用171群NVITAMIN-C库，利用PASC系统并群制作适合CEFR的6群截面数据。图4分别示出了NAS和CITATION程序堆芯计算keff的分布。其中，利用NAS进行了10 000次堆芯计算，利用CITATION进行了1 000次堆芯计算。由图4可知，两者的分布均基本符合正态，但NAS由于统计次数多，故符合得更好。

表3列出了CEFR核截面数据不确定性造成的keff不确定度结果，表中标准计算keff为采用原始数据进行单次计算所得结果。由核数据不确定性造成的不确定度为2.38%，作为比照，给出了三维蒙特卡罗微扰方法计算不确定度为2.27%，俄罗斯设计计算给出的keff不确定度为1.90%[14]，一维S-U方法计算不确定度为2.65%[15]。计算结果与参考值符合较好，其中，文献[15]及三维蒙特卡罗微扰方法所采用协方差数据与本文一致，可见，该方法所得结果与参考值中较精确的三维蒙特卡罗微扰方法的结果的相对偏差小于10%，好于一维S-U方法的。同时，NAS与CITATION两程序计算结果很接近，说明直接蒙特卡罗方法可用于不同的中子学计算程序。

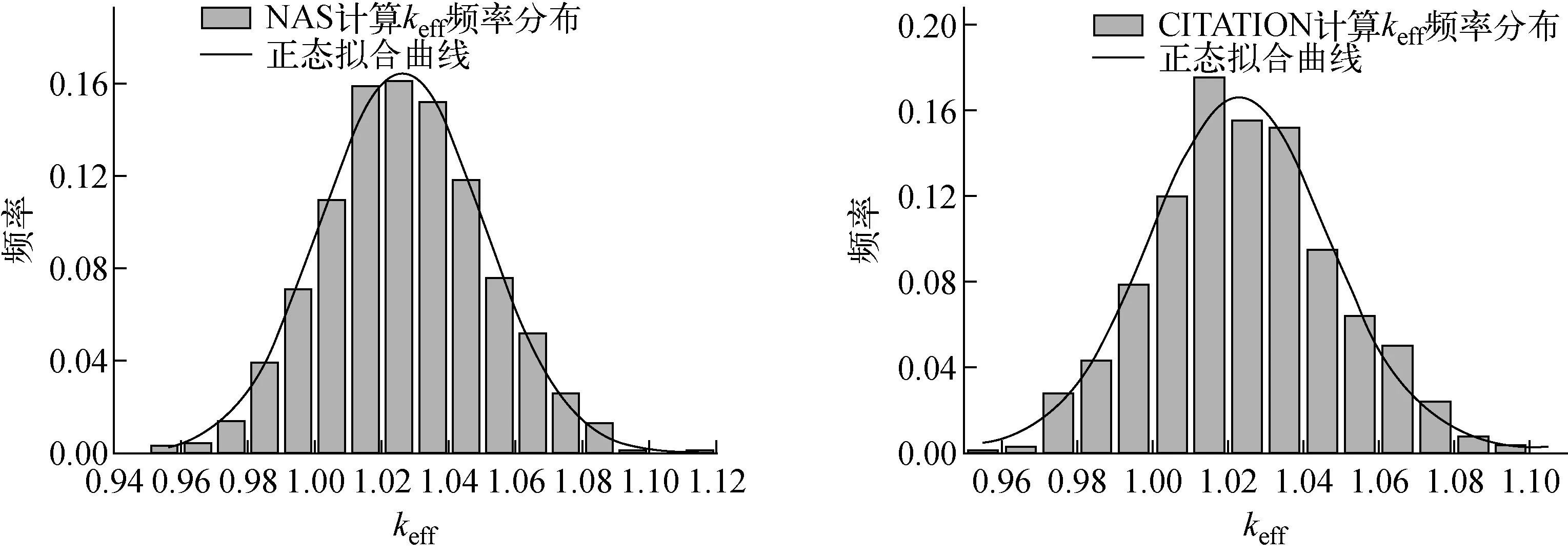
图4 NAS和CITATION计算CEFR的keff分布

表3CEFRkeff不确定度计算结果

Table3UncertaintyofcalculatedkeffforCEFR

计算程序统计keff标准计算keff相对不确定度/%95%置信度不确定度范围/%计算次数NAS1.025 81.025 92.38[2.35,2.41]10 000CITATION1.024 51.023 22.35[2.25,2.45]1 000

对于CITATION程序1 000次计算，所得95%置信区间不确定度范围为[2.25%,2.45%]，对于NAS程序10 000计算，所得95%置信区间不确定度范围为[2.35%,2.41%]，所得结果相符较好，且可满足精度要求，若需进一步减小范围，通过增加计算次数即可达到。按照蒙特卡罗统计理论，置信度区间的宽度与计算次数的0.5次方成反比[16]。由于NAS计算速度较快，故在进一步的详细计算中，只采用NAS程序。

表4列出了通过NAS计算各主要反应道不确定性造成的CEFRkeff不确定度及对比解，每种情况的计算次数为1 000次。可知，影响CEFRkeff不确定度的主要截面为235U的(n,γ)截面，其次为235U的(n,f)截面以及238U的(n,γ)截面，堆芯中核子份额较高的Na与Fe的核截面数据对整体keff不确定度的贡献很小。将计算所得6个截面的不确定度利用误差传递公式，平方相加，得出上述截面造成的总不确定度为2.39%，与直接计算总不确定度2.38%接近。这也验证了该方法既可计算单个截面造成的不确定度，也可计算多个截面造成的总不确定度。与三维蒙特卡罗微扰方法相比，结果符合较好，同时该方法能克服蒙特卡罗微扰方法存在的计算小的不确定度时统计误差偏大的缺点。

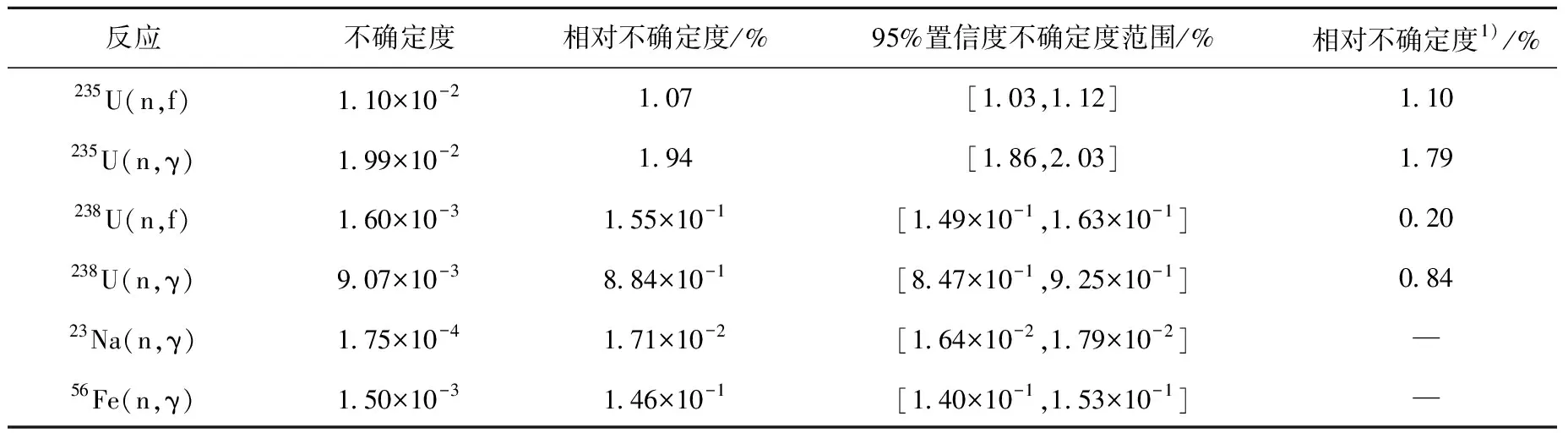
表4 NAS计算分截面核数据不确定性对CEFR keff不确定度影响

注：1) 采用MCNP微扰方法计算得到[17]，扰动量为10%

4 结论

核截面数据不确定性会引入核装置keff计算值的不确定度。直接蒙特卡罗方法可有效、简便地给出所需keff计算值的不确定度，结果合理可信。该方法的优点在于对各种装置keff求解的适应性强、可移植性好并可计算三维问题。但与所有蒙特卡罗方法相同，为达到要求精度，其计算时间长，且存在一定的随机性。随着计算机计算能力以及计算方法的不断发展，该方法的适用范围会更加广泛。

参考文献：

[1]ALIBERTI G, PALMIOTTI G, SALVATORES M, et al. Nuclear data sensitivity, uncertainty and target accuracy assessment for future nuclear systems[J]. Annals of Nuclear Energy, 2006, 33: 700-733.

[2]许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京：原子能出版社，2006.

[3]CHADWICK M B, OBLOZINSKY P, HERMAN M, et al. ENDF/B-Ⅶ.0: Next generation evaluated nuclear data library for nuclear science and technology[J]. Nuclear Data Sheets, 2006, 107(12): 2 931-3 060.

[4]BOX G, MULLER M. A note on the generation of random normal deviates[J]. The Annals of Mathematical Statistics, 1958, 29(2): 610-611.

[5]页尔骅，张德平. 概率论与随机过程[M]. 北京：科学出版社，2005.

[6]茆诗松，程依明，濮晓龙. 概率论与数理统计教程[M]. 北京：高等教育出版社，2004.

[7]李庆扬，王能超，易大义. 数值分析[M]. 5版. 北京：清华大学出版社，2008.

[8]张棣芳. CITATION程序说明书与使用说明[M]. 北京：核工业核电软件中心，1995.

[9]李泽华. 三维节块法程序在快堆物理计算中的应用[C]∥第八届反应堆数值与粒子输运学术会议. 深圳：[出版者不详]，2000.

[10] International handbook of evaluated criticality safety benchmark experiments, NEA/NSC/DOC(95)03[M].US: Nuclear Energy Agency Nuclear Science Committee of the Organization for Economic Cooperation and Development, 2006.

[11] 方邦城，唐忠樑，赵金坤. PASC-1程序系统各模块功能介绍及其输入(卡)中文说明合订本，CEFRRLP1.2-CX/PASC-1[R]. 北京：中国原子能科学研究院，2006.

[12] 胡泽华，王佳，孙伟力，等. 基准模型keff对核数据的灵敏度分析及不确定度量化[J]. 原子能科学技术，2013，47(增刊):312-317.

HU Zehua, WANG Jia, SUN Weili, et al. Sensitivity and uncertainty analysis of calculatedkeffon benchmark models due to uncertainties of nuclear data[J]. Atomic Energy Science and Technology, 2013, 47(Suppl.): 312-317(in Chinese).

[13] 田和春. 中国实验快堆堆芯设计说明，CEFR01Z19LWS01-SM[R]. 北京：中国原子能科学研究院，2002.

[14] 库扎夫考夫 Н Г，法拉克欣 М Р，拉玖内切娃 А А，等. CEFR堆芯物理特性计算误差分析[R]. 俄罗斯：[出版者不详]，2002.

[15] 刚直. 核截面引起积分参数keff不确定度的一维分析程序开发[D]. 北京：中国原子能科学研究院，2006.

[16] ROBERT C P, CASELLA G. Monte Carlo statistical methods[M]. 2nd ed. New York: Springer, 2004.

[17] 刘萍. 核数据不确定性对ADS系统keff等积分量的影响和WIMS 82群库的研制[D]. 北京：中国原子能科学研究院，2004.