高温气冷堆中间换热器层流边界层的传热特性分析
吴彦楠,董玉杰,原 鲲
(清华大学 核能与新能源技术研究院 先进反应堆工程与安全教育部重点实验室,北京 100084)
在高温气冷堆(HTR)中间换热器的研究中,以提高紧凑式换热器换热效率、降低流道总阻力为目标,确定换热器管壳两侧流道的尺寸和表面形状,是非常关键的研究内容。经调研,结合俄罗斯OKBM型板翅式换热器及美国WEC-NGNP型印刷电路板式换热器(PCHE)的优缺点,提出了以人为粗糙度强化传热为核心机理的板翅式换热器[1]。
在强化传热中,边界层传热是影响最大的传热过程,如何降低层流边界层及湍流黏性底层的厚度,从而使流动传热由热传导转变为效率更高的对流传热[2-3],是边界层研究的重要内容。欲确定人为粗糙度的形状、尺寸等条件,首先要清楚在HTR中间换热器的换热单元中,氦气作为工质的边界层传热特性。因此,本文通过对氦气在换热单元流道内的层流边界层研究,主要就层流流动边界层和热边界层的厚度进行理论计算,并通过CFD模拟对边界层内的传热特性进行分析,期望在以后设计出具有最佳强化传热效率的人为粗糙度,从而为高温堆中间换热器的强化传热提供理论依据。
1 层流边界层厚度的精确解
综合考虑俄罗斯的OKBM及美国的WEC-NGNP方案后,确定中间换热器换热单元的流道长度为150 mm,宽度为50 mm,考虑到球床高温堆粉尘生成量远高于棱柱堆[3-4],流道的高度采用WEC-NGNP的高度,为2.6 mm(图1)。在工质的参数选择方面,采用额定工况为温度900 ℃、压力7 MPa、流速19.71 m/s的氦气流。壁面温度设为恒定壁温700 ℃,从而决定边界层内流体物性参数的定性温度为边界层的算术平均温度800 ℃。具体选择的工况参数及氦气的物性参数列于表1[5]。

图1 板翅式中间换热器单元流道示意图
1.1 流动边界层
根据中间换热器流道的具体环境条件,利用边界层速度分布的相似性,可得层流边界层的微分方程。为简单起见,考虑定常平面流动、沿x轴零压梯度、忽略质量力的不可压缩黏性流体,具体方程[6]为:
(1)
相应的边界条件可设为:1) 在板面上,y=0,vx=vy=0;2) 在边界层外边界上,y=δ,vx=v(主流速度),同时有∂vx/∂y=0,∂2vx/∂y2=0。

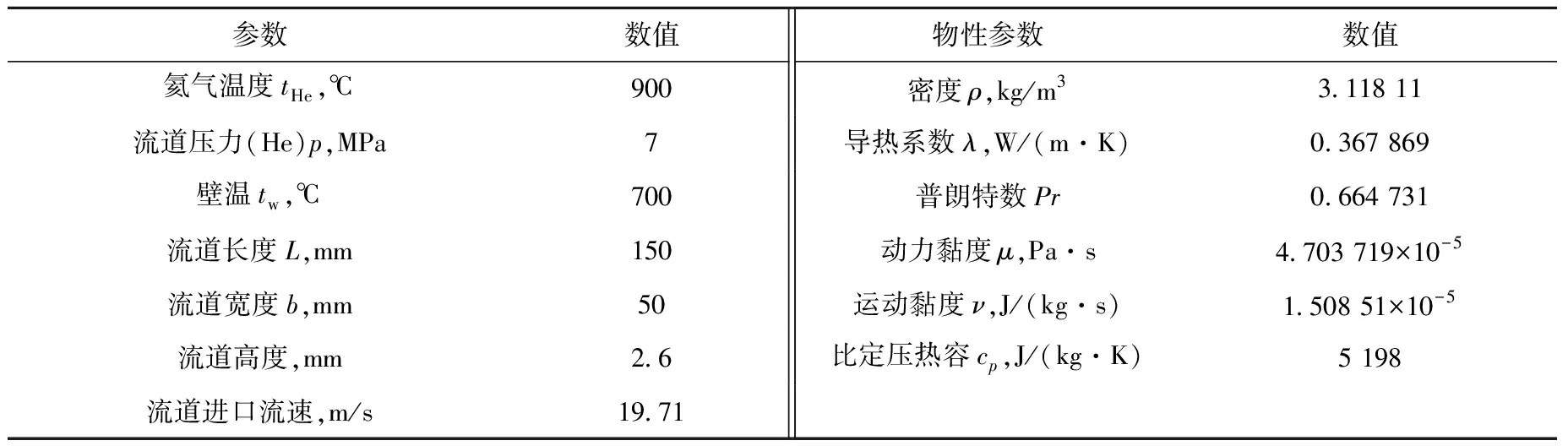
表1 中间换热器单元流道的具体参数及氦气物性参数
一次多项式:
二次多项式:
三次多项式:
四次多项式:
其中:η为无因次坐标,η=y/δ;F(η)为无因次速度,是边界层内的流向速度与主流速度的比值。将表1中中间换热器流道的具体参数及He气流的物性参数代入上面的多项式边界层厚度计算式,得到层流的流动边界层厚度(图2a)。随着流体的流动,流体与前缘点的距离增大,流动边界层厚度随之增大,但梯度逐渐变小。这是由于流体黏性的存在,使边界层内的速度梯度沿流动方向逐渐减小,从而边界层的厚度不断增加。在本文的具体流道中,边界层在流道中部、距前缘点约60 mm处便已超过流道的中心高度。根据上、下平板的对称性,此时上边界层与下边界层在流道中心相遇,流道中心区域主流流速的均匀分布转变为抛物线分布,形成泊肃叶流动。此外,在图中可明显看出二次式、三次式的速度分布较一次式、四次式更为接近Blasius的精确数值解。得到精度较高的近似速度分布,可为研究特定流道的边界层情况提供参考。
1.2 热边界层
在传热条件下,主流与壁面之间存在温度差。实验观察表明,在壁面附近的一薄层内,流体温度在壁面的法线方向上发生剧烈的变化,而在此薄层之外,流体的温度梯度几乎等于零。这一薄层即称为温度边界层或热边界层,其厚度记为δt,一般将过余温度为来流过余温度的99%处定义为δt的外边界[8]。在式(1)的基础上增加能量守恒方程:
(2)
并给定相关的温度边界条件,便可得到流动边界层与热边界层的关系式:δ/δt≈Pr1/3,其中Pr可代入表1中的数值,具体如图2b所示,可见热边界层的厚度在数量级上与流动边界层相当,但距前缘点同一距离处热边界层的厚度要大于流动边界层厚度,这说明在本文的工况中氦气流的动量扩散能力要低于热扩散能力。
2 模拟结果
在单元流道内层流边界层换热的模拟中,采用等效处理后的二维模拟结果是可接受的。本文以计算流体力学软件ANSYS-CFX为工具,建立了中间换热器单元流道的层流边界层换热模型,模型采用workbench-meshing划分的非结构化网格,网格单元总数合计为81 054。CFX中选择层流laminar模型,入口为均匀沿程流速、温度为900 ℃的高温氦气流,上、下为恒温壁面的边界条件,出口设置为7 MPa的外场条件。计算时选择并行计算,残差为1×10-6,迭代步上限为3 000。

a——流动边界层;b——热边界层
图3示出模拟结果的整体温度分布,可明显看出热边界层在图中的分布。温度在边界层内急剧升高,边界层厚度逐渐增大;待至流道末端,主流温度的区域已远小于进口端。从图4中也可得到验证,随着流动的进行,主流温度区越来越窄。根据上节的计算结果,流道末端流动已进入泊肃叶形式,热边界层的分界已无法明显看出。将模拟值与Blasius精确解进行对比,可发现在流道中部之前(<0.08 m),模拟值与精确值的热边界层厚度拟合较好;在这个区域,模拟情况可近似看成三次式的速度分布,如图5所示,两者与Blasius解的差距较小。随着流动的进行,当到达流道中部时,上、下边界层的相遇使流动进入泊肃叶形式,此时流动已无明显的边界层可言,主流区域的温度也基本保持不变,局部换热也已充分进行。

a——进口端附近;b——出口端附近
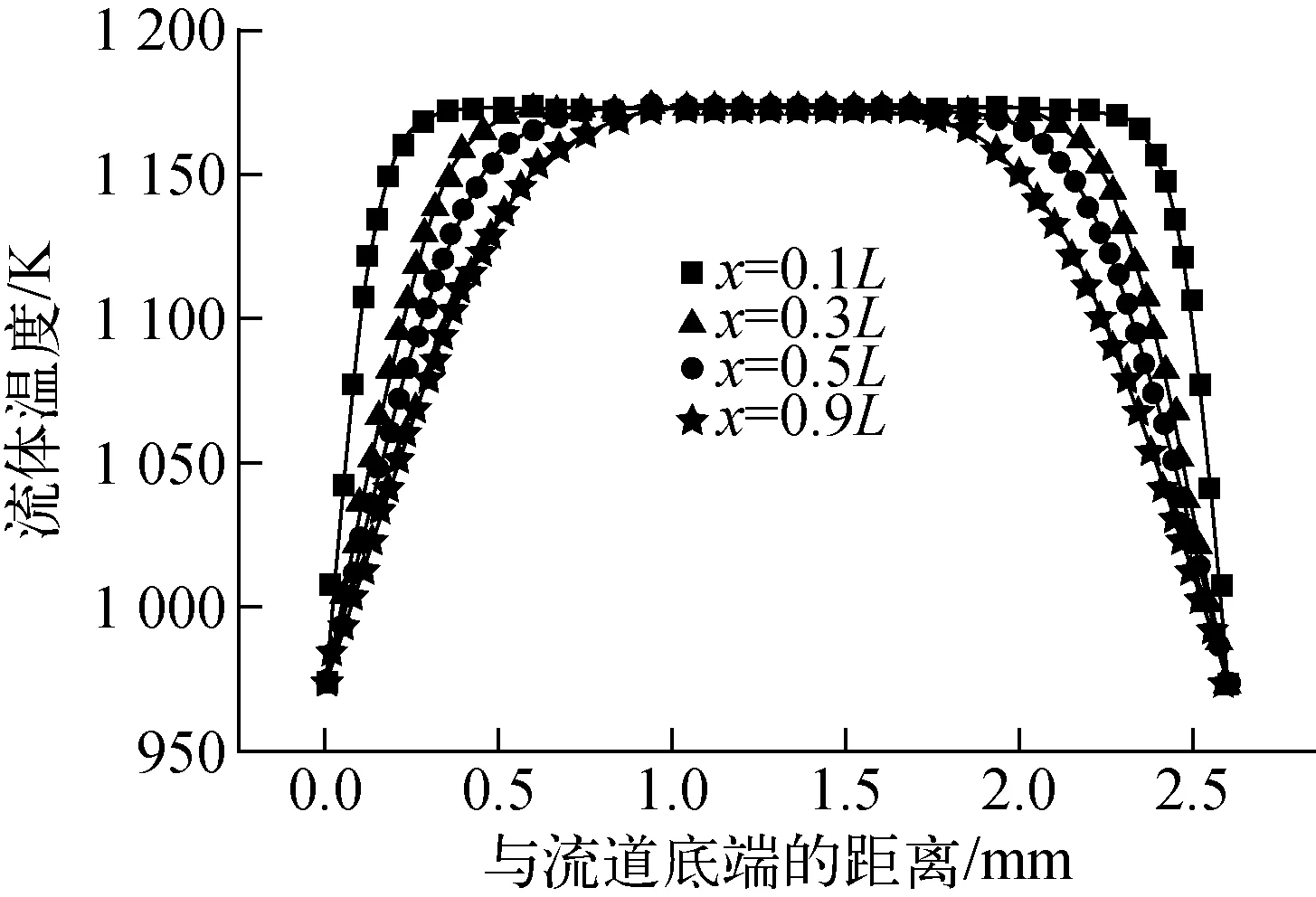
图4 不同位置的温度分布
3 边界层的传热特性

图5 模拟结果和计算结果的对比
边界层对于流体的传热,包括热传导和对流换热起着关键性影响,流体的传热大部分是在边界层区域进行,有必要对层流边界层在本文具体流道中的传热特性进行分析。图6示出不同出口压力对于中间换热器流道的壁面传热系数的影响,从图6a可看出,随Re的增大,Nu也逐渐增大,符合层流换热的理论公式。且在同一Re下,压力越低,Pr越大,导致Nu也越大。在壁面传热系数方面,如图6b所示,上、下边界层在距流道前缘点0.3 mm处相遇,从而进入泊肃叶流动,此后壁面传热系数基本保持不变,稳定在2 800 W/(m2·K)左右;同时,根据泊肃叶定律[8-9],压力的增大使氦气的黏度随之增大,进而整个流道的流阻增大,一定程度上降低了壁面传热系数。
不同氦气进口温度对传热系数的影响如图7所示,相比较而言,进口温度的影响相比出口压力要小一些,高温、高压条件下,压力对于气体黏度的作用要更明显。氦气进口温度在边界层区域和泊肃叶流动区域,对壁面传热系数均基本无影响,传热系数稳定在2 800 W/(m2·K)左右。综上可发现,不论是出口压力还是进口温度,在层流边界层中,对于流道的传热效果已无明显的提高作用,这为后期开展人为粗糙度的研究,使层流向湍流尽快转变,从而改进传热效果,提供了相关参考。
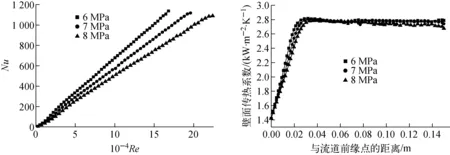
图6 出口压力对壁面传热系数的影响

图7 氦气进口温度对壁面传热系数的影响
此外,还对壁面温度的设定进行了研究,根据模拟出的壁面热流结果,将上文所述的恒定壁温条件变为恒定热流密度的边界条件,可对壁面温度的变化有所了解。Simonis等[10-11]已证明,恒定热流密度加热通道内的层流充分发展区的壁面温度沿流动方向呈线性变化,本文的模拟结果如图8所示。很明显,壁面温度的变化可分为边界层区和泊肃叶区两个线性变化区,在边界层流动区,壁面温度的变化趋势更为剧烈,这表明传热主要集中在这个区域[12]。在泊肃叶流动区,壁面温度呈缓和线性递减。边界层区和泊肃叶流动区的转折点与模拟值和计算值中达到流道中心的边界层厚度值吻合较好。总体的壁温变化范围为750~900 ℃左右,而此前模拟的恒温条件为700 ℃,是可接受的。
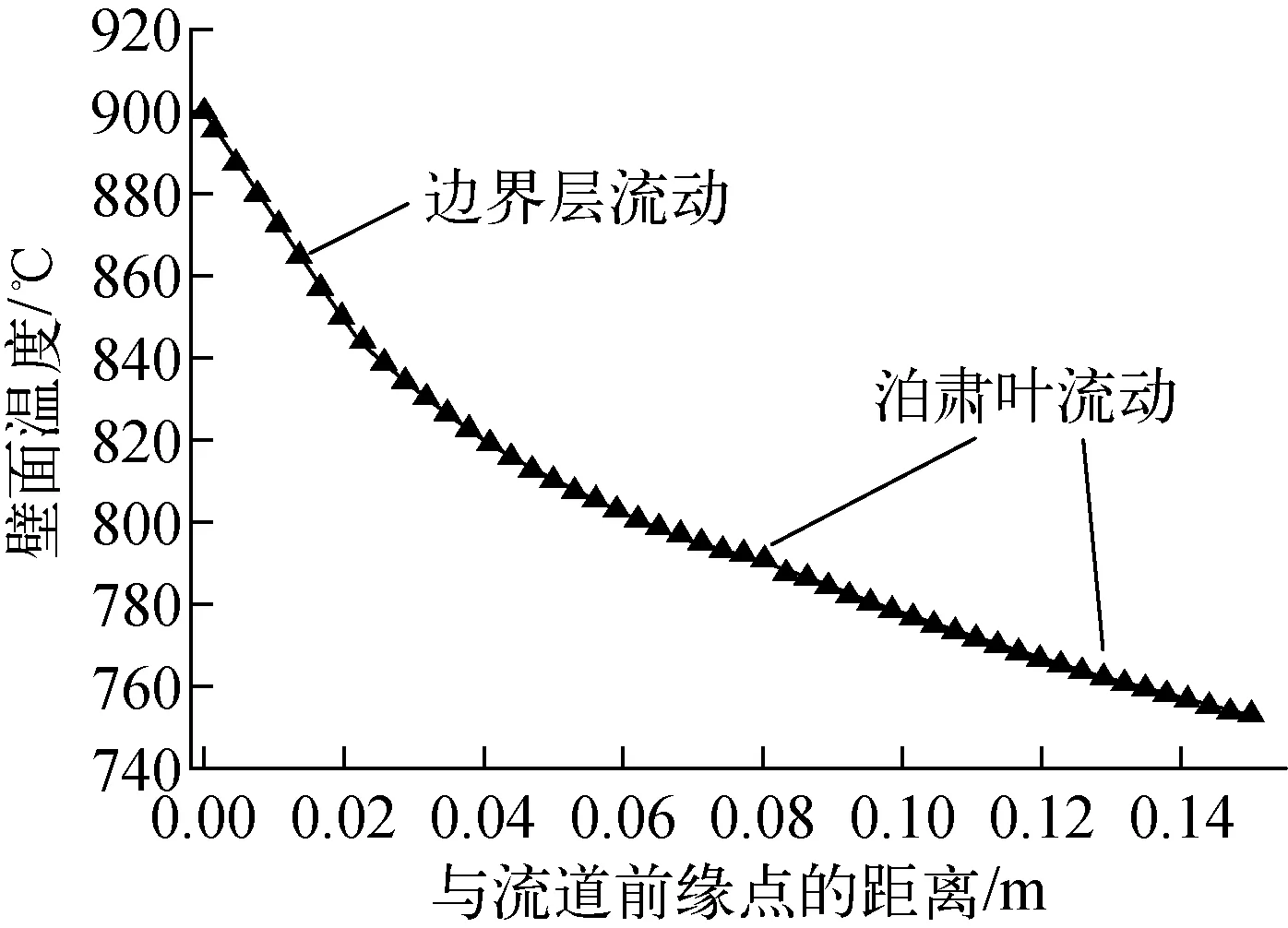
图8 壁面温度的变化
4 小结
本文主要对高温气冷堆中间换热器单元流道的层流流动边界层及热边界层进行了理论计算和模拟分析。利用幂次多项式速度分布的方法,对流道内的层流边界层进行了计算,结果表明,三次式的速度分布更为接近Blasius精确解,也更为符合数值模拟的结果。同时,在流道中部,上、下边界层的相遇会使流动进入泊肃叶的抛物线形式。
通过模拟还发现,氦气的进口温度和出口压力对于层流边界层的换热基本无影响,传热系数稳定在2 800 W/(m2·K)左右,这为以后进行湍流和人为粗糙度的强化传热研究提供了基础。同时,恒定热流密度下,壁面温度的变化分为明显的边界层区和泊肃叶区,这是本文流道的显著特点,在这两个区域壁面温度呈线性变化。
参考文献:
[1]吴彦楠,董玉杰. 高温堆中间换热器流道的层流流动边界层研究[C]∥全国第十三届反应堆热工流体学术会议. 上海:[出版者不详],2013:45-47.
[2]MOON S K, BAEK W P, CHANG S H. Parametric trends analysis of the critical heat flux based on artificial neural networks[J]. Nuclear Engineering and Design, 1996, 163(1): 29-49.
[3]STEPHEN J D. The development of high efficiency heat exchangers for helium gas cooled reactors[R]. USA: Idaho National Laboratory, 2002.
[4]WRIGHT J K. NGNP heat exchangers materials research and development plan[R]. USA: Idaho National Laboratory, 2008.
[5]居怀明. 载热质热物性计算程序集数据手册[M]. 北京:原子能出版社,1990.
[6]孔珑. 工程流体力学[M]. 3版. 北京:中国电力出版社,2007.
[7]彭一川. 平板层流边界层的最佳近似速度分布[J]. 东北工学院学报,1992,13(1):56-61.
PENG Yichuan. Optimal approximation velocity profile in a laminar boundary layer on flat plate[J]. Journal of Northeast University of Technology, 1992, 13(1): 56-61(in Chinese).
[8]章梓雄. 黏性流体力学[M]. 北京:清华大学出版社,2011.
[9]杨世铭,陶文铨. 传热学[M]. 4版. 北京:高等教育出版社,2011.
[10] SIMONIS V, POSKAS P. Enhancement of heat transfer and hydraulic drag in gas-cooled helical channels with artificial roughness[J]. Nuclear Engineering and Design, 2012, 245: 153-160.
[11] KAYS W, CRAWFORD M, WEIGAND B. Convective heat and mass transfer[M]. New York: McGraw-Hill Company, Inc., 2005: 70-73.
[12] ROSENHEAD L. Laminar boundary layer[M]. Oxford: Oxford University Press, 1963: 270-272.

