空间电荷透镜电子云状态研究
张凤娟,张潮海
(哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001)
20世纪40年代,空间电荷透镜的概念被提出[1],直到60年代Морозов[2]才制造出空间电荷透镜。随后各种类型的空间电荷透镜出现,但原理均是采用外加电磁场将大量电子约束在透镜中,形成电子云对离子束进行聚焦,电子云的状态决定离子的聚焦性能[3]。空间电荷透镜有着不破坏束流的自中和效应及聚焦能力更强的优越性[4-5]。电子云是非中性等离子体,对磁约束的电子云可采用研究等离子体的理论方法。本文在电子的磁流体方程组的基础上推导磁镜场中电子的密度及电位分布,数值模拟中心电子密度、磁约束因子、电子温度3个参数的变化对电子云状态的影响。
1 磁镜
电子在磁场中沿磁感线漂移,磁矩具有不变性,磁镜利用了磁矩的不变性。在磁场强的位置,粒子垂直速度变大,总能量不变,所以平行速度变小,平行动能转化为垂直动能;在磁场弱的位置,垂直动能转化为平行动能。有些平行速度小的粒子会在某处丧失平行方向的动能,被该处磁场反射而向相反方向运动,到达对称位置时又被反射,从而粒子在磁镜场中来回运动,成为约束粒子。平行速度大的粒子通过线圈,成为逃逸粒子。被磁镜约束的粒子的速度分布会出现以2θm为顶角的损失锥,其中θm为中间面上粒子运动速度与磁感线夹角的临界值。锥内粒子全部逃逸出磁镜,锥外粒子被约束,被束缚的电子形成电子云。
磁镜场是轴对称磁场,在圆柱坐标系下,轴对称的磁场的磁矢势为:
(1)
式中:α=(R-1)/(R+1),R为磁镜比;k=2π/L,L为磁镜距离;B0=(Bmax-Bmin)/2α,B为磁感应强度。则磁镜场内部磁感应强度为:
(2)
式中,I0和I1为双曲型贝塞尔函数。在空间透镜的磁镜场(z,r)平面的磁感应强度分布如图1所示。

图1 (z,r)平面磁感应强度分布
2 电子云的空间电场
空间电荷透镜中电子的磁流体方程组(电子的连续性方程、动量方程、能量方程和静电场方程)[6]为:
(3)
式中:ε0为真空介电常数;κ为波尔兹曼常数。n为电子密度;m为电子质量;e为电子电量;v为电子速度;U为电子电位;B为磁场强度;T为电子温度;ν为电子碰撞频率。
空间电荷透镜中,电子密度较大,电子沿磁力线运动较沿横越磁力线容易,残余气体原子和电子的有效碰撞电离,使电子运动受到一定的阻尼,使某平磁面的电子云偏离平衡状态,最终一部分电子扩散逸出约束区域。损失电子可通过装置中的冷阴极Penning放电和杂散离子轰击管壁的电子二次发射进行补偿。由于电子的漂移运动,损失电子和补偿电子呈动态平衡状态,电子云处于一定密度的稳定状态。此时,电子在垂直于z轴的平面内绕z轴做旋轮线式运动。电子的流体运动方程为:
(4)
式中,p=γ0κTn,γ0为比热比。在流体力学中忽略极小项,得到:
(5)

(6)
式中,n0为透镜中心电子密度。空间电荷场中电子沿径向方向的密度分布为:
(7)
结合Poisson方程得到:
(8)
设理想磁镜场是以z轴对称的柱状电子云,透镜中心为原点。当电子云的轴向长度远大于径向长度时,电子云可看作无限长,由电子产生的电场抵消空间电荷场轴向分量,即∂U/∂z≈0,则式(8)简化为:
(9)
假定束轴上的电位为0,对式(9)采用四阶龙格-库塔法对二阶微分方程进行数值求解,模拟得到透镜场中的电势分布(图2)。求解过程中所需的其他参数可根据已有实验经验取定。从图2可看出,在一定的半径区域范围内电场呈线性变化,此区域的电场对穿过的离子束流起径向聚焦作用。图2示出的电子云的电势分布和文献[7]的接近。
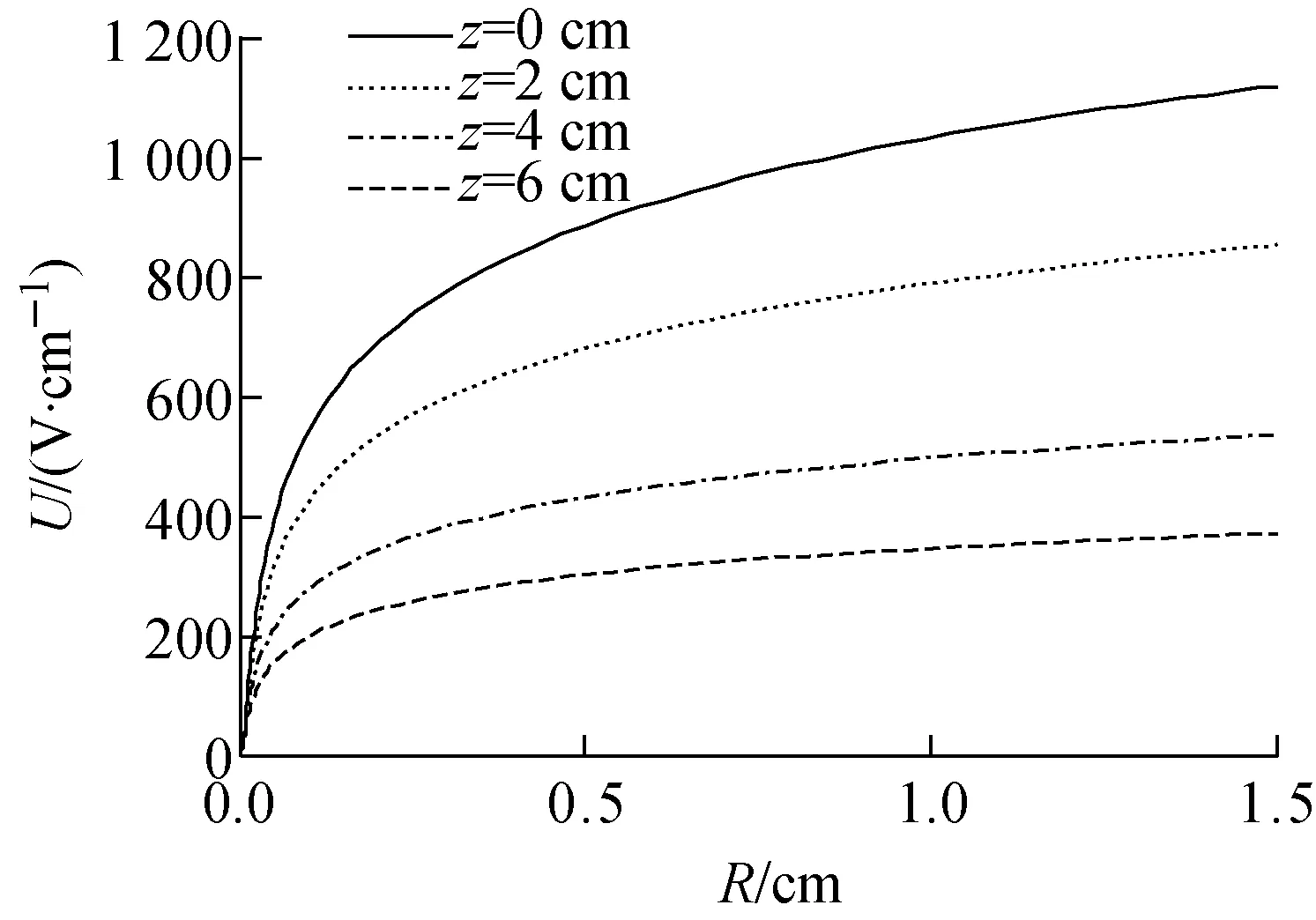
图2 电子云的电势分布
3 电子云参数
运行的空间电荷透镜中电子云的状态取决于中心电子密度n0、磁约束因子γ、T3个特征参数。这3个参数确定了电子云的空间形态和密度分布,也决定着此透镜的聚焦性能。磁约束因子为:
(10)
结合式(2)得到空间电荷透镜中轴对称磁场和磁约束因子的关系。本文所采用的磁场是磁场强度沿z轴方向逐渐增加的轴对称磁场。磁约束因子沿z轴的变化趋势如图3所示。结合图1、3和式(10)可看出,磁约束因子和磁场强度呈线性关系,变化率取决于电子密度和回旋频率,电子密度和磁约束因子之间有制约关系。结合式(7)、(9)可看出,电子云的3个特征参数相互不独立,1个参数的变化将引起其他参数的变化,电子云状态、大小和密度分布参数也会发生改变,从而会改变电子云的电场分布,对聚焦性能产生很大的影响。

图3 n0=1015 m-3时磁约束因子沿z轴的变化
(11)
电子云内,∂n/∂r<0,故γ>0。对式(11)取不同γ、T得到图4。
从图4a可看出,透镜中心轴附近的电子密度越高,电子密度沿径向近似于线性的变化率减少,电极边缘附近,电子密度几乎无变化。电子温度取某定值时,相同数量的电子γ越大,电子云半径被压缩得越小,电场对电子的约束能力越强;从图4b可看出,在透镜中心轴附近区域,沿径向有一小段电子密度几乎不变,随后沿径向以较大的变化率减少。γ取某定值时,电子温度越高,电子运动越活跃,电子在空间电荷透镜中的弥散状态越明显,电子在整个电荷空间透镜中分布越均匀。中心轴附近区域,电子运动活跃碰撞几率较大,但由于密度较大,加之线性电场的约束,电子难以逃出此区域;电极附近区域电子密度较低,电子运动碰撞几率较低,活动范围较大。

图4 γ(a)、T(b)对电子云状态的影响
4 结论
本文阐述了轴对称磁镜场约束电子的理论,得到磁镜场新型的空间电荷透镜的理论基础。对轴对称磁镜场的磁矢势进行理论模拟,绘制(z,r)平面内磁场强度的分布。在新型空间电荷透镜磁场中,在电子损失和补偿呈动态平衡的基础上得到某密度平衡态的电子云。结合电子的磁流体运动方程组,推导出绝热状态下空间电荷透镜中电子的波尔兹曼分布,将电子的波尔兹曼分布和Poisson分布结合进行四阶龙格-库塔二阶微分方程求解,得到空间电荷透镜中电势的分布。离子聚焦性能取决于电子云,而电子云的3个参数对电子云的状态起决定作用。引入磁约束因子关系式,得到轴对称磁镜场中磁约束因子沿z轴方向近似于线性的变化趋势。结合式(7)、(10)可看出,电子云的3个状态参量相互制约,改变电子云的状态,对聚焦性能有很大的影响。对磁约束因子、电子温度取不同的数值进行对比研究,结果表明,磁约束因子的约束能力以及电子运动活跃程度,对电子云的状态有着较大的影响。
参考文献:
[1]GIBSON G, JORDAN W C, LAURE E J. Particle behavior in static, axially symmetric, magnetic mirror and cups geometries[J]. Phys Fluids, 1963, 6(1): 116-133.
[2]МОРОЗОВ А И. Вопросы теории плазма[J]. Атомиздат, 1974, 7(8): 247-381.
[3]BOOTH R, LEFEVER H W. Space charge lens for high current ion beams[J]. Nucl Instrum Methods, 1978, 151: 143-147.
[4]孙别和. 空间电荷中和透镜的研究[J]. 原子能科学技术,1991,25(2):52-56.
SUN Biehe. Study of space charge neutralization lens[J]. Atomic Energy Science and Technology, 1991, 25(2): 52-56(in Chinese).
[5]刘承俊,刘烈刚,马跃,等. 强流电子束在螺旋管下的聚焦[J]. 强激光与粒子束,1991,3(3):384-390.
LIU Chengjun, LIU Liegang, MA Yao, et al. Characteristics of an intense electron beam focused by a solenoid lens[J]. High Power Laser and Particle Beams, 1991, 3(3): 384-390(in Chinese).
[6]郁庆长. 理想长空间电荷透镜中的电子云[J]. 原子能科学技术,1987,21(6):666-670.
YU Qingchang. Electron cloud in ideal long space-charge lens[J]. Atomic Energy Science and Technology, 1987, 21(6): 666-670(in Chinese).
[7]ЗАВАЛОВA М. Особенности формированя объё-много заряда в сильноточной плазменной линзе[J]. Вопросы Атомной Науки И Техники, 2003, 7(3): 60-62.

