电导非线性对HVDC电缆绝缘空间电荷动态过程的影响
孙云龙 李忠华 索长友

摘 要:针对HVDC电缆绝缘中的空间电荷问题,采用有限元分析方法,仿真研究绝缘材料电导非线性属性对HVDC电缆绝缘中由非线性电导率引起的空间电荷极化与退极化动态过程的影响。通过改變电导活化能与电场依赖系数,得到极化与退极化过程中空间电荷密度随时间的变化规律。分析结果表明:降低电导活化能或增大电场依赖系数可降低HVDC电缆绝缘中由非线性电导率引起的空间电荷量,抑制极化与退极化过程中的空间电荷“过冲”与“反极性过冲”现象,并且会加快极化与退极化过程达到稳态,但同时会使绝缘介质中的电流密度增大。
关键词:非线性电导;HVDC电缆;空间电荷;极化;动态过程
中图分类号:TM 854
文献标志码:A
文章编号:1007-449X(2019)07-0027-11
Abstract:In order to research the space charge problems caused by nonlinear conductivity in HVDC cable insulation, the finite elements method was adopted to study the effect of nonlinear conductivity attributes on dynamic process of space charge polarization and depolarization in HVDC cable insulation. The space charge density patterns during polarization and depolarization over time were attained while changing the conductivity activation energy and the fielddependent coefficient. The results show that reducing the conductivity activation energy or increasing the fielddependent coefficient diminishes the space charge amount and the “overshoot” during polarization and depolarization which are all induced by nonlinear conductivity and also makes the polarization and depolarization reach the steady more quickly. But meanwhile that increases the current density in cable insulation.
Keywords:nonlinear conductivity; HVDC cable; space charge; polarization; dynamic process
0 引 言
直流输电技术在大容量、高电压、远距离输电中具有诸多优于交流输电技术的优势[1-2]。作为直流输电系统中的关键组成部分,聚合物绝缘高压直流(highvoltage directcurrent, HVDC)电缆,尤其是交联聚乙烯(crosslinked polyethylene, XLPE)高压直流电缆得到了广泛应用[3]。而XLPE HVDC电缆中的空间电荷问题一直备受关注[4-6]。
根据空间电荷的来源[7],可将其非为两类:一类是产生在强电场下取决于绝缘材料微观特性(如绝缘介质中杂质的热电离、极性分子的极化、电极的注入、陷阱等因素)的空间电荷;另一类由材料宏观介电参数在空间变化而形成的慢极化引起的空间电荷,它的产生与绝缘材料电导率非线性属性、结构参数、温度梯度和外施电压等多种因素有关。针对第一类空间电荷,国内外有许多学者作了深入研究[8-13]。而对于第二类空间电荷,现有的空间电荷测试技术并不能将二者区分开来[14-16],并且第二类空间电荷在数值上也相对很小[17-18],常常会被忽略,因此有关后者的研究相对较少。但后者可存在于任何场强下,同样影响着HVDC电缆运行时绝缘中的电场分布。探明绝缘材料的电导非线性属性对HVDC电缆绝缘空间电荷极化与退极化动态过程的影响规律,对于新型绝缘材料的开发具有重要指导意义。
本文采用多物理场耦合软件Comsol Multiphysics,仿真研究了不同的电导非线性属性对HVDC电缆绝缘中空间电荷极化与退极化动态过程的影响。
1 模型建立
1.1 仿真模型
为了研究绝缘介质电导的非线性属性对HVDC电缆绝缘中空间电荷极化与退极化动态过程的影响,参考320 kV,500 MW直流电缆典型结构[19],对其进行简化后建立如图1所示的HVDC电缆仿真模型,模型中内电极半径为26 mm,绝缘介质厚度为24 mm,外电极半径为52 mm。
1.2 材料属性、边界条件与加载方式
1.2.1 材料属性
模型求解时各部分材料属性如表1所示。
1.2.2 温度场的确定
由于HVDC电缆在实际运行中导体线芯发热,将会在电缆绝缘中产生温度梯度,为使仿真条件更接近实际情况,模型中温度边界条件的设定如表2所示。
式中:Rin、Rout分别是内、外电极半径;r是绝缘介质中任意一点处半径。
本文中ΔT=30 K,绝缘介质中相应的温度分布曲线如图1所示。
1.2.3 电场边界条件的确定
外电极接地,内电极施加由下式确定的激励电压。
1.3 数值求解方法
采用软件COMSOL Multiphysics有限元软件中的瞬态求解器对模型求解,其本质是对泊松方程进行数值求解过程。数值求解过程中,空间网格剖分单元大小和时间步长是影响求解精度的关键因素。对计算区域进行三角网格剖分时,剖分单元最大尺寸设定值为0.2 mm。为了充分保证极化和退极化过程能达到稳态,计算时间为1 400 000 s,其中前400 000 s为极化过程,后1 000 000 s为退极化过程。为了保证计算精度和缩短计算时间,采取分时段设定计算步长,具体设置如表3所示。
1.4 空间电荷的求取
COMSOL Multiphysics有限元软件计算结果可直接提供空间电荷密度ρ的时空分布,但由于存在模型误差(由边界剖分网格精细程度决定),空间电荷密度ρ在电极边界处的分布明显和物理事实不符。为此,由电位移D的整体时空分布,通过线性插值推算出电极附近受模型误差影响处的电位移D,进一步计算出空间电荷密度ρ的时空分布,具体关系式为
2 空间电荷极化建立过程
2.1 电导活化能对空间电荷极化过程的影响
电导率式(1)中的各个参数由文献[20]给出:A=3.278 1 V/(Ω·m2),B=2.77×10-7 m/V。在ΔT=30 K,U0=300 kV的条件下仅改变电导活化能φe使其分别为0.5、0.52、0.54、0.56、0.58和0.6 eV,由此仿真得到不同电导活化能条件下绝缘介质在极化过程中的电场与空间电荷密度时空分布,典型结果如图3、图4所示。
在相近的温度和场强条件下,空间电荷密度数值与文献[21-22]中实测结果在同一数量级。由图3、图4可知,在极化过程中由于温度梯度的存在使得稳态时电场出现翻转(稳态时电缆绝缘中电场呈现内低外高分布形式),空间电荷随时间变化出现“过冲”现象,即空间电荷密度随极化时间先增加后减小最后趋于稳态值的非单调现象。
极化过程空间电荷的产生是介质电导率在空间呈梯度分布的结果,不同位置电荷密度随时间的变化过程由下式[20]決定:
空间电荷的动态行为很大程度取决于松弛时间的时空分布情况。由计算得到松弛时间τ(t, r)的典型时空分布如图5所示。
从图5可以看出,介质的动态松弛时间在任意时刻沿半径方向均呈现内低外高的分布形式;施加电压之初动态松弛时间的空间分布梯度高于稳态时动态松弛时间空间分布梯度。在内电极施加正极性电压时,带正电的载流子由内电极向外电极迁移,由于内导体附近r处松弛时间小于r+Δr处松弛时间,r处电荷迁移速率大于r+Δr处电荷迁移速度,因此而形成正极性空间电荷的积累,同时正电荷的积累反过来降低了r处的电场,并使电导率下降,载流子迁移速率下降,这是一个负反馈过程,因此最终达到稳态。整体表现出空间电荷密度的“过冲”行为[24]。
不同的电导活化能条件下对应的绝缘介质中稳态空间电荷密度平均值如图6所示。由图6知,随着电导活化能的增大,绝缘介质中稳态空间电荷积累量呈线性增加。
为了能清晰地体现出不同的电导活化能对绝缘介质中空间电荷极化过程的影响,分别在绝缘介质r=26.2、38、49.8 mm处提取空间电荷密度,得到空间电荷密度随时间变化的曲线,如图7所示。
由图6、图7可知,活化能越大,空间电荷“过冲”现象出现的越慢,“过冲”峰值越大,稳态空间电荷密度越大。
由跳跃电导模型推导得到的电导率公式(1)中的活化能φe直接影响载流子的迁移率μ[25],
外加激励相同的条件下,活化能越大则迁移率越小,对外界激励的响应也就越慢,因此会导致空间电荷“过冲”现象出现得越慢;并且活化能越大,电导率受温度影响越大,相同的温度梯度下,形成的电导率梯度也越大,而极化空间电荷稳态值由式(5)可得,
由式(7)知,稳态空间电荷密度正比于松弛时间梯度,而电导率梯度越大,松弛时间梯度也越大。因此,活化能越大,稳态时绝缘介质中空间电荷密度越大。
提取极化过程中绝缘介质单位长度吸收电流(极化总电流减去电导电流),得到吸收电流随时间变化曲线及其半衰期(吸收电流衰减至初始值的一半所需时间),如图8所示。其中电流半衰期可反映极化(退极化)过程达到稳态的快慢。
由图7可知,活化能增大,吸收电流随之减小,并且极化达到稳态所需时间在增加。这也正是由于电导活化能增大使得载流子迁移率减小,同等外界条件下的电导率减小,电流密度随之减小;并且载流子迁移速率也在减小,因此极化达到稳态所需时间增加。
2.2 电场依赖系数对空间电荷极化过程的影响
在ΔT=30 K,U0=300 kV,A=3.278 1 V/(Ω·m2),φe=0.56 eV的前提下,改变电场依赖系数B,在其分别等于1.27×10-7、1.77×10-7、2.27×10-7、2.77×10-7、3.27×10-7和3.77×10-7 (单位:m/V)的条件下进行仿真,得到不同电场依赖系数时对应的绝缘介质中电场与空间电荷密度时空分布,典型结果如图9、图10所示。
对比图9和图3、图10与图4可知,增大电场依赖系数B使得绝缘介质中由温度梯度导致的电场翻转程度有所缓和,并且绝缘中整体空间电荷密度有所下降。这一点由图11稳态平均空间电荷密度与电场依赖系数的关系曲线可以更清楚地体现。
图12为分别在绝缘介质r=26.2 mm、r=38 mm和r=49.8 mm处提取空间电荷密度,得到不同电场依赖系数时空间电荷密度随时间变化的曲线。
从图12中可知,增大电场依赖系数会抑制空间电荷“过冲”行为,降低了绝缘介质中的总体空间电荷积累量,并且使极化达到稳态所需时间缩短。电场依赖系数增大将会有助于绝缘介质内的电场均匀分布 [26-27],使得绝缘介质中的电场模在径向上的梯度减小,进而使得空间电荷密度动态过程变化有所缓和。
图13为不同的电场依赖系数下绝缘介质中吸收电流随时间变化曲线及其半衰期。
由图13可知,电场依赖系数越大,相应的极化电流也越大,极化达到稳态所需时间越短。这是因为电场依赖系数增大时,同等外界条件下绝缘介质对应的电导率也随之增大[26-27]。
3 空间电荷退极化耗散过程
3.1 电导活化能对空间电荷退极化过程的影响
改变电导活化能φe使其分别为0.5、0.52、0.54、0.56、0.58和0.6 eV,其他条件与极化过程相同。仿真得到不同电导活化能条件下绝缘介质退极化过程电场与空间电荷密度时空分布,典型结果如图14、图15所示。
在退极化过程中会出现空间电荷“反极性过冲”现象,即内电极附近空间电荷不是随时间单调减小到零,而是出现反极性的峰值而后再衰减到零。退极化过程的“反极性过冲”与极化过程的“过冲”相互呼应,“反极性过冲”仍是由动态松弛时间的时空分布所决定的。由于退极化过程内电极附近出现反向电场,故出现“反极性过冲”。
圖16为不同活化能对不同位置空间电荷退极化动态特性的影响。由图可知,电导率活化能对退极化过程空间电荷“反极性过冲”现象的影响规律与极化过程一致,即活化能越大,空间电荷“反极性过冲”现象出现得越慢,“反极性过冲”峰值越大。
由图17退极化电流密度随时间变化曲线以及退极化电流半衰期与活化能的关系曲线同样可知,活化能对空间电荷退极化过程的影响规律与极化过程相同。
3.2 电场依赖系数对空间电荷退极化过程的影响
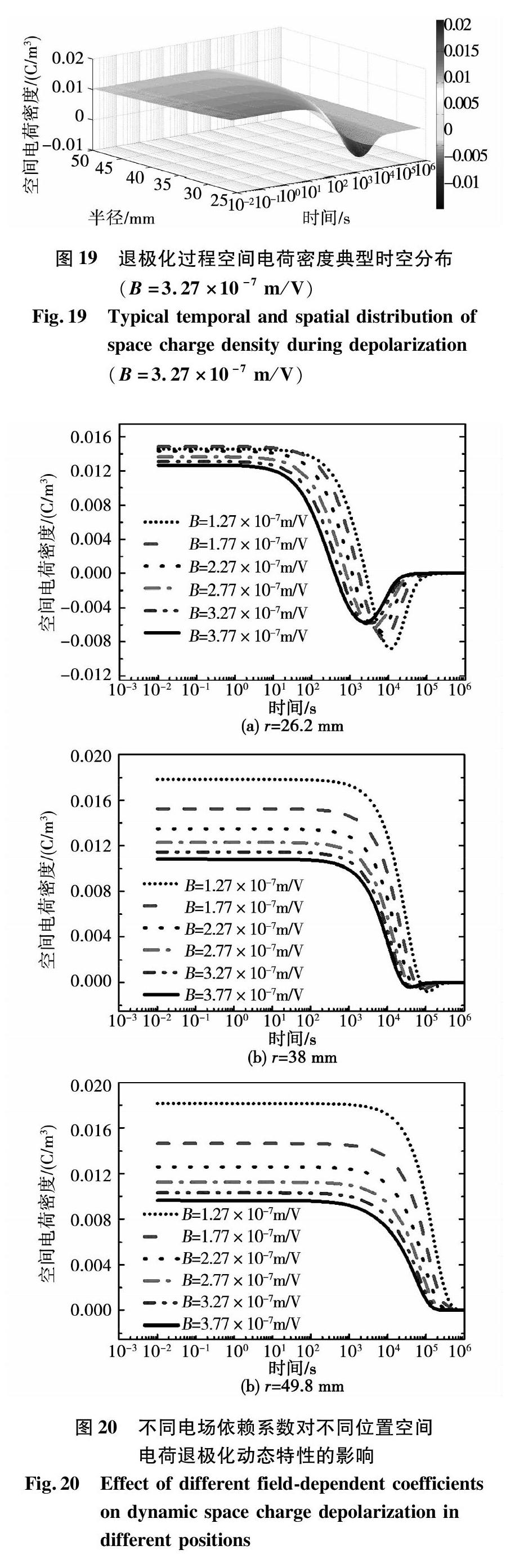
改变电场依赖系数B,在其分别等于1.27×10-7、1.77×10-7、2.27×10-7、2.77×10-7、3.27×10-7和3.77×10-7 (单位:m/V),其他条件同极化过程。在此条件下进行仿真,得到此时电场与空间电荷密度典型时空分布如图18、图19所示。
图为20不同电场依赖系数对不同位置空间电荷退极化动态特性的影响。
由图20可知,改变电场依赖系数对空间电荷“反极性过冲”现象的影响规律与极化过程一致,即增大电场依赖系数会抑制空间电荷“反极性过冲”行为,并且使退极化达到稳态所需时间缩短。
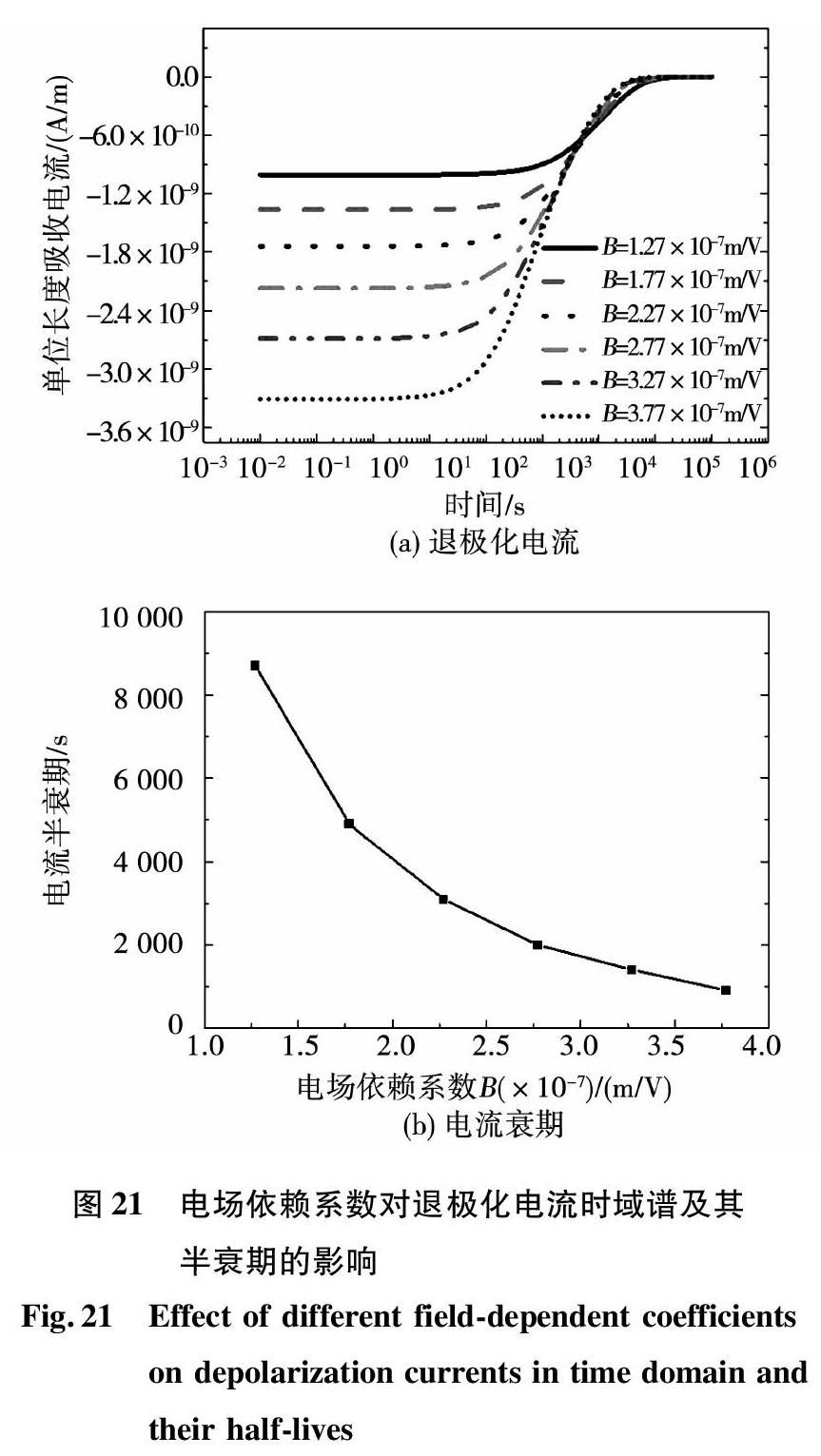
由图21不同电场依赖系数时的退极化电流及其半衰期曲线也可以看出电场依赖系数对空间电荷极化与退极化影响规律相同。
4 结 论
利用 COMSOL 软件对HVDC 电缆在确定的结构、外加激励形式和绝缘层温度梯度条件下电缆绝缘中的空间电荷极化与退极化动态过程仿真,得出如下结论:
1)降低绝缘材料电导活化能,可以减少极化过程绝缘介质中由非线性电导引起的空间电荷积累量,并抑制极化与退极化过程中空间电荷“过冲”与“反极性过冲”行为,同时使极化与退极化达到稳态所需时间缩短;
2)增大电场依赖系数同样可以可降低空间电荷积累量,抑制空间电荷极化和退极化过程中的“过冲”与“反极性过冲”行为,缩短极化、退极化达到稳态所需时间。
参 考 文 献:
[1] 温家良,吴锐,彭畅,等. 直流电网在中国的应用前景分析[J]. 中国电机工程学报, 2012, 32(13):7.
WEN Jialiang, WU Rui, PENG Chang, et al. Analysis of DC grid prospects in China[J]. Proceedings of the CSEE, 2012, 32(13):7.
[2] 张翀,查俊伟,王思蛟,等. 高压直流绝缘材料的发展与展望[J]. 绝缘材料,2016,49(2):1.
ZHANG Chong, ZHA Junwei, WANG Sijiao, et al. Development and outlook of insulating materials for high voltage direct current cables[J]. Insulation Materials, 2016,49(2):1.
[3] 何金良,党斌,周垚,等. 挤压型高压直流电缆研究进展及关键技术述评[J]. 高电压技术,2015, 41(5):1417.
HE Jinliang, DANG Bin, ZHOU Yao, et al. Reviews on research progress and key technology in extruded cables for HVDC transmission[J]. High Voltage Engineering, 2015, 41(5):1417.
[4] 吴锴,陈曦,王霞,等. 温度梯度下电缆绝缘中空间电荷特性的研究现状[J]. 绝缘材料,2012,45(3):60.
WU Kai, CHEN Xi, WANG Xia, et al. Research situation of space charge characteristic in cable insulation under temperature gradient[J]. Insulation Materials, 2012, 45(3):60.
[5] MONTANARI G C. Bringing an insulation to failure: the role of space charge[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2001, 18(2):339.
[6] MAZZANTI G, MONTANARI G C. Quantities extracted from spacecharge measurement as markers for insulation aging[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(2):198.
[7] 仇斌,何军,屠德民. 直流交联聚乙烯绝缘中空间电荷的形成机理[J]. 绝缘材料,2010,43(6):39.
QIU Bin, HE Jun, TU Demin. Formation mechanism of space charges in DC XLPE insulation[J]. Insulation Materials, 2010,43(6):39.
[8] HOZUMI N, SUZUKI H, OKAMOTO T. Direct observation of timedependent space charge profiles in XLPE cable under high electric fields[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1994, 1(6):1068.
[9] 陈曦,王霞,吴锴,等. 温度梯度场对高直流电压下聚乙烯中空间电荷及场强畸变的影响[J]. 电工技术学报,2011,26(3):13.
CHEN Xi, WANG Xia, WU Kai, et al. Space charge accumulation and stress distortion in polyethylene under high dc voltage and temperature gradient[J]. Transactions of China Electrotechnical Society, 2011,26(3):13.
[10] 吴锴,朱庆东,陈曦,等. 温度梯度效应对油纸绝缘材料空间电荷分布特性的影响[J]. 高电压技术,2011,37(4):823.
WU Kai, ZHU Qingdong, CHEN Xi, et al. Effect of temperature gradient on space charge distribution in oil impregnated papers[J]. High Voltage Engineering, 2011, 37(4):823.
[11] 付一峰, 陈俊岐, 赵洪, 等. 交联聚乙烯接枝氯乙酸烯丙酯直流介电性能[J]. 电工技术学报, 2018, 33(18): 4372.
FU Yifeng, CHEN Junqi, ZHAO Hong, et al. DC dielectric properties of crosslinking polyethylene grafted chloroacetic Acid Allyl Ester[J]. Transactions of China Electrotechnical Society, 2018, 33(18):4372.
[12] 李亚莎, 代亚平, 花旭, 等. 杂質对交联聚乙烯电缆内部电场和空间电荷分布影响[J]. 电工技术学报, 2018, 33(18): 4365.
LI Yasha, DAI Yaping, HUA Xu, et al.The influence of impurities on electric field and space charge distribution in XLPE cable[J]. Transactions of China Electrotechnical Society, 2018, 33(18):4365.
[13] 闫志雨, 赵洪, 韩宝忠, 等. 基于α松弛分析CB/LDPE纳米复合介质空间电荷特性[J]. 电机与控制学报, 2017, 21(06): 50.
YAN Zhiyu, ZHAO Hong, HAN Baozhong, et al. Analysis of the space charge characteristic of CB /LDPE nanocomposites from the view of α relaxation[J]. Electric Machines and Control, 2017, 21(06):50.
[14] XU Xiaoxiao, LEI Zhipeng, SONG Jiancheng, et al. Development of the space charge measurement techniques based on pulsed electricacoustic method for HVDC power cables[C]// 2016 IEEE International Conference on High Voltage Engineering and Application, Sept. 19-22, 2016, Chengdu, China. IEEE, 2016: 1-4.
[15] AHMED N H, SRINIVAS N N. Review of space charge measurements in dielectrics[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1997, 4(5):644.
[16] 王亚林,吴建东,易姝慧,等. 固体介质空间电荷与松弛电流的同步测量及应用研究[J]. 中国电机工程学报, 2017, 37(3):931.
WANG Yalin, WU Jiandong, YI Shuhui, et al. Simultaneous measurement and application of space charge and relaxation current for solid dielectric[J]. Proceedings of the CSEE, 2017, 37(3):931.
[17] Mcallister I W, CRICHTON G C, PEDERSEN A. Space charge fields in dc cables[C]// 1996 IEEE International Symposium on Electrical Insulation, June 16-19, 1996, Montreal, Quebec, Canada. IEEE, 2002:661-665.
[18] FABIANI D, MONTANARI G C, BODEGA R. The effect of temperature gradient on space charge and electric field distribution of HVDC cable models[C]// 2006 IEEE 8th International Conference on Properties and Applications of Dielectric Materials, June 26-30, 2006, Bali, Indonesia. IEEE, 2007:65-68.
[19] 杨佳明,王暄,韩宝忠,等. LDPE 纳米复合介质的直流电导特性及其对高压直流电缆中电场分布的影响[J]. 中国电机工程学报, 2014, 34(9):1454.
YANG Jiaming, WANG Xuan, HAN Baozhong, et al. DC conductivity characteristic of LDPE nanocomposite and its effect on electric field distribution in HVDC cables[J]. Proceedings of the CSEE, 2014, 34(9):1454.
[20] BOGGS S, DAMON D H, HJERRILD J, et al. Effect of insulation properties on the field grading of solid dielectric DC cable[J]. IEEE Transactions on Power Delivery, 2001, 16(4):456.
[21] HOLBOLL J T, HENRIKSEN M, HJERRILD J. Space charge buildup in XLPE cable with temperature gradient[C]// 2000 Annual Report Conference on Electrical Insulation and Dielectric Phenomena.Victoria, Canada, 2000: 157-160.
[22] BAMBERY K R, FLEMING R J, HOBOLL J T. Space charge profiles in low density polyethylene samples containing a permittivity/conductivity gradient[J]. Journal of Physics D: Applied Physics, 2001, 34(20): 3071-3077.
[23] MCALLISTER I W, CRICHTON G C, PEDERSEN A. Charge accumulation in DC cables: A macroscopic approach[C]// Conference Record of the 1994 IEEE International Symposium on Electrical Insulation, June 5-8, 1994, Pittsburgh, USA. IEEE, 2002: 212-216.
[24] SUN Yunlong, LI Zhonghua, SUO Changyou, et al. A simulation on space charge distribution caused by nonlinear conductivity in HVDC cable insulation[C]// 2017 International Symposium on Electrical Insulating Materials, September 11-15, 2017, Toyohashi, Japan. IEEE, 2017: 126-129.
[25] 陳季丹,刘子玉. 电介质物理学[M]. 北京:机械工业出版社,1982: 209-213.
[26] 李忠华,刘乐乐,郑欢,等.HVDC电缆电场分布影响因素的仿真研究[J]. 中国电机工程学报,2016,36(9):2563.
LI Zhonghua, LIU Lele, ZHENG Huan, et al. Simulation on the influence factors of electric field distribution in HVDC cable[J]. Proceedings of the CSEE, 2016, 36(9): 2563.
[27] 郑欢,刘乐乐,李忠华. 直流叠加冲击电压下HVDC电缆暂态电场分布特性研究[J]. 中国电机工程学报,2016,36(24):6682.
ZHENG Huan, LIU Lele, LI Zhonghua. Research on the transient electric field distribution in HVDC cable under DC voltage superimposed impulse voltages[J]. Proceedings of the CSEE, 2016, 36(24):6682.
(编辑:刘素菊)

