生成非Cross簇的最小幺半群
李永康,张文婷
(1.诺瓦东南大学数学、科学与科技系,美国 佛罗里达 33314;2.兰州大学数学与统计学院,甘肃 兰州 730000)
一个有限生成的,有限基的且包含有限多个子簇的代数簇称作Cross簇.由有限群[1]、 有限环[2-3]、有限李代数[4]生成的簇都是Cross簇.但是这一结果对一般代数并不成立,比如3阶的交换半群S={1,2,3},其乘法表如下:
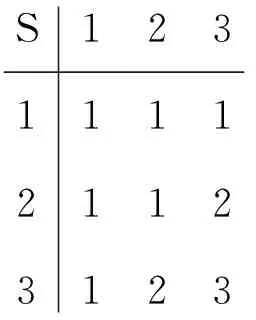
S123111121123123
由S生成的半群簇包含无限多个子簇[5],故它是非Cross簇.此外不同构于半群S的所有阶数小于等于3的半群都生成Cross半群簇[6].因此,在同构意义下,S是生成非Cross半群簇的最小阶数的半群.
半群S同时也是幺半群,而当焦点由半群簇转移到幺半群簇时情形却完全不同,因S生成一个仅有3个子簇的Cross幺半群簇,由此可知所有阶数小于等于3的幺半群生成的幺半群簇都是Cross簇.在此基础上,本文将对生成非Cross幺半群簇的幺半群的最小阶数是多少进行研究.
定理在同构和反同构的意义下,生成非Cross幺半群簇的最小幺半群仅有一个:5 阶幺半群M5={1,2,3,4,5},其乘法表如下:
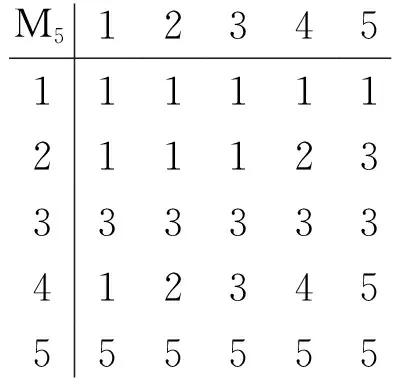
M512345111111 211123 333333 412345 555555
本文在第3节将证明幺半群M5生成一个非Cross幺半群簇,在第4节证明其他所有小于等于5阶的幺半群都生成Cross幺半群簇.从而定理得证.
1 预备知识
对任意的变元集X,记X*为X上的自由幺半群,X*上的元素称作字.用u≈v表示等式,其中u和v都是字.称幺半群M满足等式u≈v,如果对于映射到M的任意替代φ都有φ(u)和φ(v)相等.称幺半群M满足等式集Σ,如果M满足Σ中所有等式.
设U是所有满足等式集Σ的幺半群组成的类,则称U为Σ定义的幺半群簇,Σ为U的一个等式基.称幺半群类U为幺半群簇,如果U是某个等式集定义的幺半群簇.等价地,一个幺半群类U是幺半群簇当且仅当U在同态像、子幺半群和任意直积运算下封闭[7].由一类幺半群生成的簇是包含这个幺半群类的最小簇.
称一个簇是有限基的,如果它有一个有限的等式基.称一个簇是有限生成的,如果它可以由一个有限代数生成.一个有限生成的,有限基的且包含有限多个子簇的簇称作Cross簇.
引理1任意一个Cross簇的所有子簇都是Cross簇.
证明参阅文献[8]中定理2.1.
关于簇和泛代数的更多信息可以参阅文献[9].
2 由M5生成的幺半群簇
由M5生成的幺半群簇记作5,由等式集
xhxtx≈xhxt,
(1)
xhytxy≈xhytyx,
(2)
xy2z2x2≈x2y2z2x2
(3)
引理2对任意的n≥0,幺半群簇不满足等式
pn≈qn,
其中
x0h(x1x0x2x1…xn+1xn)txn+1
和
x0hx1(x1x0x2x1…xn+1xn)txn+1.
证明将等式集(1)~(3)应用到字pn,则得到的字的形式必然为
x0hx1w0x2w1…xn+1wntwn+1,
其中wi∈{x0,…,xi}*xi{x0,…,xi}*.故等式集(1)~(3)不能将字pn转化为qn,于是簇不满足等式pn≈qn.
引理3设M是幺半群簇中任意一个有限幺半群且|M| 其中 1≤j 令 则 即M满足等式pn≈qn. 命题1幺半群簇是非有限生成的. 证明如果幺半群簇是有限生成的,那么由引理3可知对于某个n,它满足等式pn≈qn,这与引理2矛盾. 本节将证明除了同构或反同构于M5的幺半群之外,所有小于等于5阶的幺半群都生成Cross幺半群簇. 引理4设M是满足等式 xyx≈x2y (4) 或者 xyx≈yx2 (5) 的任意一个有限幺半群,则M生成一个Cross幺半群簇. 证明设M是满足等式(4)的任意一个有限幺半群,且是由M生成的幺半群簇.由于幺半群M是有限的,故必然存在某个n≥1,使得幺半群簇满足等式x2n≈xn.于是包含有限多个交换子簇[11].另外由文献[12]中命题4.1可知,簇包含的非交换子簇也是有限多个.从而包含有限多个子簇,由文献[13]中引理7可知是Cross幺半群簇. 由对称性可知,满足等式(5)的任意有限幺半群也生成一个Cross幺半群簇. 引理5设M是满足等式集 (6) 或者 (7) 的任意一个幺半群,则M生成一个Cross幺半群簇. 证明设幺半群A={1,2,3,4,5},其乘法表如下: 由文献[14]中命题3.2(c)可知,等式集(6)是由A生成的幺半群簇的一个等式基.因为A是一个完全正则幺半群且它的幂等元构成一个正则带,所以幺半群簇包含有限多个子簇[15],从而是一个Cross幺半群簇.显然满足等式集(6)的任意幺半群生成的簇都是的子簇,故由引理1可知它是Cross幺半群簇. 由对称性可知,满足等式集(7)的任意幺半群也生成一个Cross幺半群簇. 引理6[16]满足等式 xyxzx≈xyzx (8) 的任意幺半群生成一个Cross幺半群簇. 引理7满足等式集 (9) 的任意幺半群生成一个Cross幺半群簇. 证明设幺半群B={1,2,3,4,5},其乘法表如下: B12345111111211122311133412345513254 由文献[14]的命题3.2(d)和文献[17]的引理7.1可知,等式集(9)是由B生成的幺半群簇的一个等式基.由文献[17]中定理7.2的证明可知,的任意真子簇都满足等式(4).因此由等式集(4)和(9)定义的簇是幺半群簇的唯一极大真子簇,由引理4可知是Cross簇.从而是一个Cross幺半群簇.显然满足等式集(9)的任意幺半群生成的簇都是的子簇,故由引理1可知它是Cross幺半群簇. 命题2所有小于等于 4阶的幺半群都生成Cross幺半群簇. 证明在同构和反同构的意义下,存在27个4阶幺半群[18].例行地可以验证这些幺半群每一个都满足式(4)~(7)中的某个等式集,故由引理4和5可知结论成立. 命题3在同构和反同构的意义下,除了M5之外,所有 5阶幺半群都生成Cross幺半群簇. 证明设M是既不同构也不反同构于M5的任意一个5阶幺半群.由文献[17]中第5节可知幺半群M满足式(4)~(9)中的某个等式集,故由引理4~7可知结论成立. [1] Oates S,Powell M B.Identical relations in finite groups [J].J Algebra,1964,1:11-39. [2] Kruse R L.Identities satisfied by a finite ring [J].J Algebra,1973,26:298-318. [3] L′vov I V.Varieties of associative rings.I [J].Algebra and Logic,1973,12:150-167. [4] Bahturin Y A,Ol′shanski A Y.Identical relations in finite Lie rings [J].Math USSR-Sb,1975,25:507-523. [5] Evans T.The lattice of semigroup varieties [J].Semigroup Forum,1971,2:1-43. [6] Luo Y F,Zhang W T.On the variety generated by all semigroups of order three [J].J Algebra,2011,334:1-30. [7] Birkhoff G.On the structure of abstract algebra [J].Proc Cambridge Philos Soc,1935,31:433-454. [8] MacDonald S O,Vaughan-Lee M R.Varieties that make one Cross [J].J Austral Math Soc Ser A,1978,26:368-382. [9] Burris S,Sankappanavar H P.A course in universal algebra [M].New York:Springer Verlag,1981. [10] Lee E W H,Li J R.Minimal non-finitely based monoids [J].Dissertationes Math:Rozprawy Mat,2011,475:3-65. [11] Head T J.The varieties of commutative monoids [J].Nieuw Arch Wisk,1968,16(3):203-206. [12] Lee E W H.Maximal Specht varieties of monoids [J].Mosc Math J,2012,12:787-802. [13] Lee E W H.Almost Cross varieties of aperiodic monoids with central idempotents [J].Beitr Algebra Geom,2013,54:121-129. [14] Edmunds C C.On certain finitely based varieties of semigroups [J].Semigroup Forum,1977,15:21-39. [15] Gerhard J A,Petrich M.All varieties of regular orthogroups [J].Semigroup Forum,1985,31:311-351. [16] Lee E W H.Varieties generated by 2-testable monoids [J].Studia Sci Math Hungar,2012,49:366-389. [17] Edmunds C C,Lee E W H,Lee K W K.Small semigroups generating varieties with continuum many subvarieties [J].Order,2010,27:83-100. [18] Sloane N J A.The on-line encyclopedia of integer sequences[EB/OL].2013-06-21.http:∥oeis.org/A058133.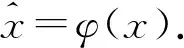

3 其他幺半群生成的簇



