考虑渗透率张量的各向异性油藏流线模拟方法

冯其红,王 相,王端平,王延忠

(1.中国石油大学石油工程学院,山东青岛266580；2.中国石化胜利油田分公司,山东东营257015)

流线数值模拟方法通过将油藏三维问题转化为一系列沿流线的一维问题进行求解，和传统数值模拟方法相比，流线模型不存在数值弥散和不稳定性，计算速度快，允许节点多，减少了网格方位的影响，同时，通过流线分布可以形象地显示注采井的生产动态关系[1-5]。基于以上特点，流线模拟越来越广泛地应用于油藏开发中，并表现出巨大的潜力。随着油田开发的不断进行，渗透率各向异性渗流问题越来越受到人们的重视[6-8]。传统的流线模拟方法[9-11]均假设渗透率主方向与坐标轴方向相同，采用向量形式的渗透率，若渗透率主方向与坐标轴方向不一致，采用向量形式将产生较大误差[12-13]。对于各向异性油藏渗流问题，建立能够处理全张量形式渗透率的流线模拟方法，对油藏动态进行准确模拟和预测，对此类油藏合理高效地开发具有十分重要的理论价值和实际意义。笔者对具有全张量形式渗透率的非均质油藏流线数值模拟问题进行研究，首先推导全张量渗透率情况下流线模型压力方程并进行求解，然后给出全张量渗透率下流线确定方法和饱和度场计算方法，最后进行实例分析。

1 压力方程及其数值求解

1.1 基本假设

在推导全渗透率张量情况下流线模型压力方程时，假设：①油藏中渗流为等温渗流；②油藏中流体为油水两相，每一相的渗流均符合广义达西定律；③忽略毛管力和重力的影响；④岩石和流体均不可压缩；⑤油藏渗透率为完全各向异性，即油藏区域每一点O处存在对应的渗透率张量K，用全张量形式表示为

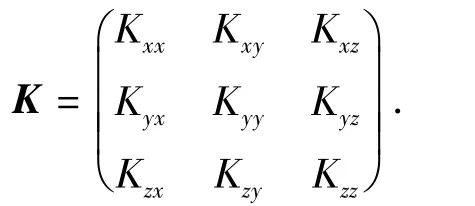
K为对称矩阵，即Kij=Kji。

1.2 压力方程的建立

三维两相渗流时达西定律可以表示为

式中，下标l=w，o分别代表水相和油相；vl为l相的流速，m/s；pl为l相的压力，MPa；μl为l相的黏度，mPa·s；Krl为l相的相对渗透率。

物质守恒方程为

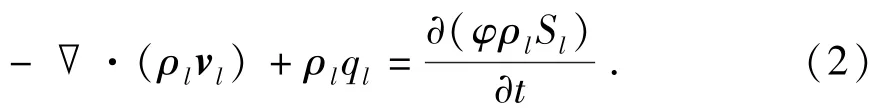
式中，ρl为l相的密度，kg/m3；Sl为l相的饱和度；φ为孔隙度。

将式(1)带入式(2)，得渗流方程为

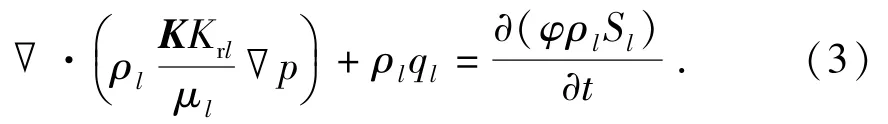
对于不可压缩岩石和流体，有，不考虑毛管力，即pw=po=p。带入渗流方程有

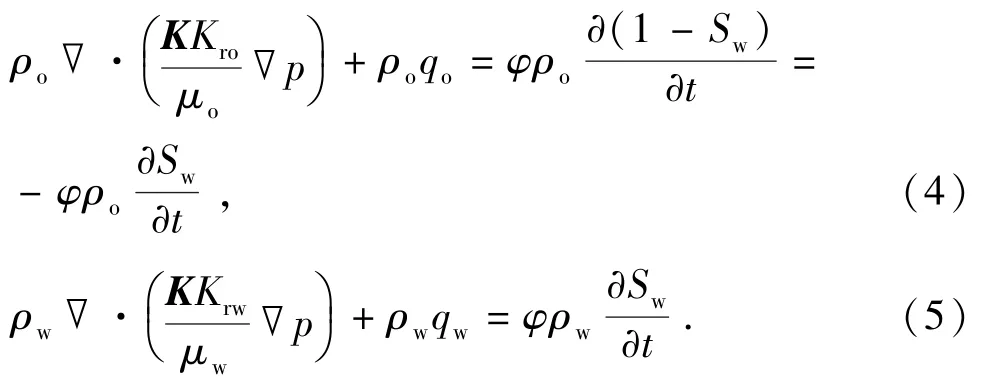
两式相加有

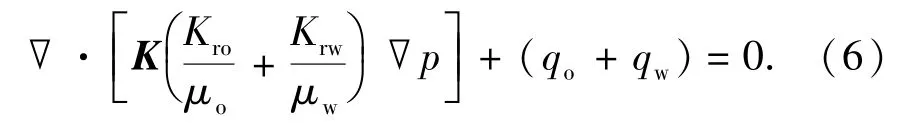
式(6)即为考虑全张量渗透率流线模型的压力方程。

对应压力方程的定解条件包括边界条件和初始条件。边界条件包括内边界条件和外边界条件。流线模型中一般将外边界考虑成不渗透边界，因此外边界条件可以表示为

内边界条件分为定压和定产两种情况。定产条件为

定压条件为

初始条件，即给出初始状态时油藏饱和度分布，表示为

根据压力方程(5)和相应的定解条件(7)～(10)即可求出油藏的压力分布。

1.3 压力方程的求解

将压力方程展开，得

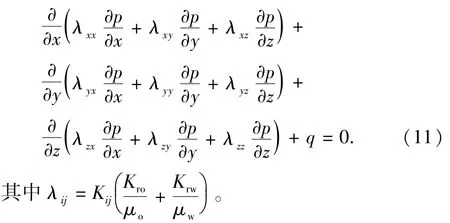
式(11)为复杂的偏微分方程，采用有限差分法对该方程进行离散。为了描述方便，接下来的公式中均认为采用块中心网格系统，正方形等距网格，使用十九点差分格式进行差分离散[14]，对于

可以证明，这种差分格式对原偏导数的逼近误差为O(Δx2)，差分后形成的方程组系数矩阵为19对角矩阵[15]。方程组采用预处理共轭梯度法求解。

2 流线的确定

流线即流场中线上每一流体质点同一时刻的速度矢量都和它相切的曲线。本文中采用Pollock方法确定并追踪流线。Pollock方法即在网格系统中压力场已知的情况下应用达西方程建立流体真实的流动速度场，在此基础上确定流线的轨迹[16]。

2.1 速度场的计算

将方程(1)写成分量形式，有

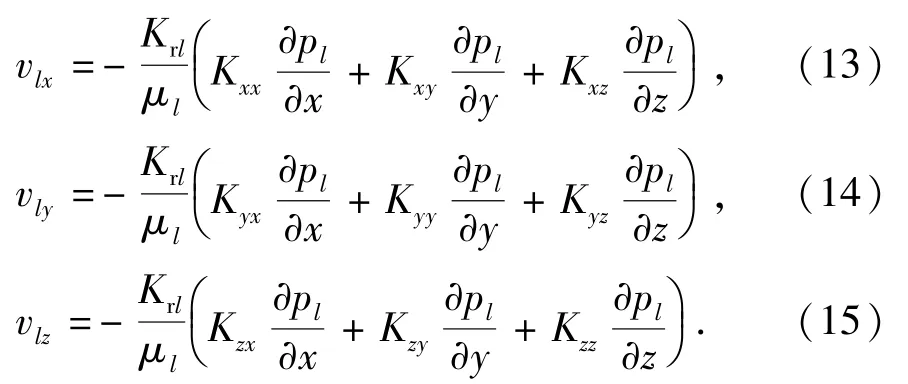
对上述方程进行差分，计算各网格边界上的速度：

网格内任一点的速度通过该网格六个界面的速度线性差值得到。网格内任意一点速度的x方向分量为

同理，可得该点速度的y方向分量vly(x，y，z)和z方向分量vlz(x，y，z)。

由于流体均不可压缩，总的真实流速即油水两相各自流速的矢量和为

2.2 确定流线

对于定常运动，迹线与流线重合，因此通过研究从注入井发出并收敛于生产井的流体质点的空间运动轨迹即可确定流线。

设(x，y，z) 是网格(i，j，k) 中任一给定点，经过该点的流线必定穿过网格某一界面并与界面存在交点(x*，y*，z*)。其中到达界面需要的时间为

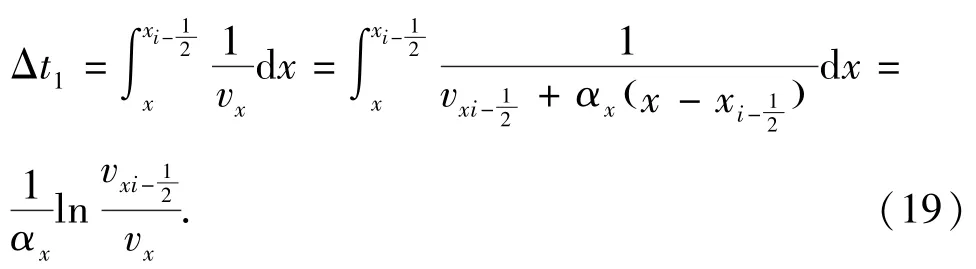
同理，到达其他界面需要的时间分别为

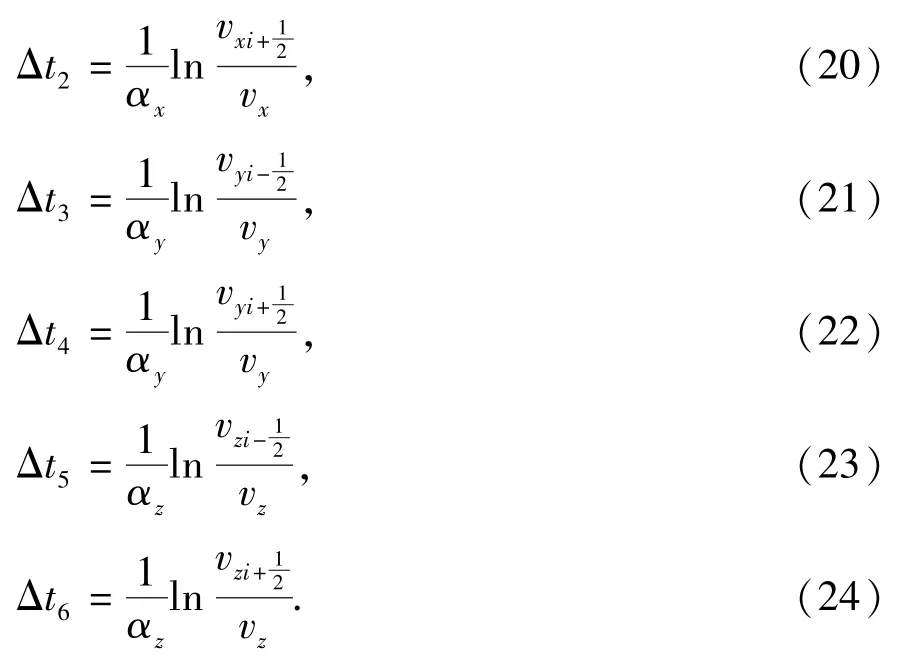
这些值可能取正、负或零值，其中正值表示点(x*，y*，z*) 位于点(x，y，z) 的下游，负值表示点(x*，y*，z*) 位于点(x，y，z) 上游，零值表示两点位于同一界面上。实际上Δt即上述6个值中最小正值，记为

求出Δt后便可求出流出点位置(x*，y*，z*)：

这样，根据已知的速度场，从注入井网格出发，逐段求解，直至生产井网格，就可以得到整条流线的轨迹。

3 计算饱和度场

由Buckley-Leverett驱油理论，在某条流线内，有

定义传播时间τ为

进而可以得到

沿流线方向，有

结合式(33)和(34)，带入式(30)可以得到

使用数值方法进行求解，有

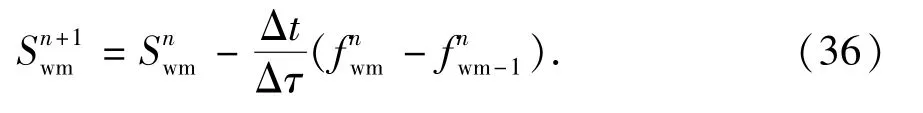
求解出油水相的压力场和速度场后就可以根据式(35)求解沿流线饱和度分布。这样就将油藏中的三维问题转换成一系列沿流线的一维问题。

4 结果分析

建立100 m×100 m的封闭油藏模型，网格为25×25×1，1口注水井位于油藏左下角，注水量为20 m3/d，1口生产井位于油藏的右上角，产液量为20 m3/d，地层孔隙度为0.25，渗透率主值分别为Kx=500 × 10-3μm2，Ky=50 × 10-3μm2。

对坐标系ox′y′绕原点进行旋转得到坐标系oxy中的渗透率张量[12，17]为

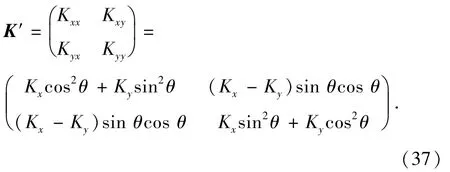
式中，θ为主渗透率方向与坐标轴方向夹角。

当θ为时，对应于oxy坐标系中的渗透率张量分别为。图1为各渗透率张量下油藏生产100 d后的压力和流线分布。从图1中可以看出，各向异性对压力和流线分布影响显著。压力沿着较大的渗透率主值方向传播较快，且流线与压力梯度方向不一致，这是由于在考虑渗透率张量后计算流速时引入了交叉项。

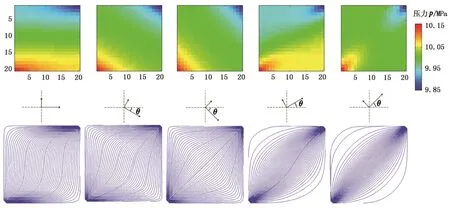
图1 各向异性油藏压力和流线分布Fig.1 Pressure and streamline distribution in different anisotropic reservoir

图2为油藏含水率随时间的变化规律。由图2中可以看出，当θ=π/4或θ=π/6时，由于最大主渗透率方向与注采井连线方向基本一致，导致注入水沿该方向迅速窜入采油井，见水时间较早。当θ=-π/4或θ=-π/6时注入水推进较均匀，见水时间晚。图3中比较了各油藏的采收率，从图3中可以看出，油藏的各向异性对注水开发的采收率影响显著。从θ=π/4和θ=π/6的流线分布可以看出，油藏左上角和右下角部分几乎没有流线经过，注入水很难驱替到该部分剩余油，从而使得采收率较低。θ=-π/4和θ=-π/6的流线在整个油藏中分布，注入水推进均匀，采收率较高。图4给出了各渗透率张量下油藏注入水突破时含油饱和度分布。

图2 各向异性油藏含水率曲线Fig.2 Water cut curves in anisotropic reservoir

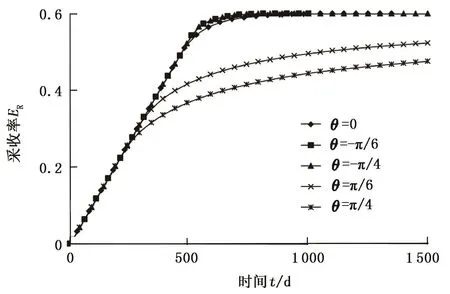
图3 各向异性油藏采收率曲线Fig.3 Oil recovery efficiency curves in anisotropic reservoir

图4 各向异性油藏饱和度分布Fig.4 Oil saturation distribution in anisotropic reservoir

5 结 论

(1)考虑渗透率张量下流线模型相比传统流线模型更加复杂。采用十九点差分格式对压力方程进行差分离散，求解压力场，采用全张量渗透率下运动方程求解速度场，由于交叉项的存在，导致全张量渗透率下速度方向与压力梯度方向一般不一致。

(2)当最大主渗透率方向与注采井方向相近时，注入水沿最大主渗透率方向突进明显，油藏中部分区域基本没有流线经过，该部分油很难被波及，开发效果较差。当最大主渗透率方向与注采井方向基本垂直时，流线均匀的分布在油藏整个区域，注入水推进均匀，开发效果较好。

[1] TONY L，KYRRE B，MARTHA C，et al.The use of streamline simulation in reservoir management：methodology and case studies[R].SPE 63157，2000.

[2] MATRINGE S F，JUANES R，TCHELEPI H A.Tracing streamlines on unstructured grids from finite volume discretizations[J].SPE Journal，2008(12)：423-431.

[3] RODRIGUEZ P G，SEGURA M K，MORENO F J M.Streamline methodology using an efficient operator splitting for accurate modelling of capillarity and gravity effects[R].SPE 79693，2003.

[4] MATRINGE S F，JUANES R，TCHELEPI H A.Robust streamline tracing for the simulation of porous media flow on general triangular and quadrilateral grids[J].Journal of Computational Physics，2006，219(2)：992-1012.

[5] PREVOST M，EDWARDS M G，BLUNT M J.Streamline tracing on curvilinear structured and unstructured grids[J].SPE Journal，2002(6)：139-148.

[6] EDWARDS M G.Simulation with a full-tensor coefficient velocity field recovered from a diagonal-tensor solution[J].SPE Journal，2000，5(4)：387-393.

[7] 刘月田.各向异性油藏注水开发布井理论与方法[J].石油勘探与开发，2005，32(5)：101-104.LIU Yue-tian.Well location in water-flooding anisotropic oil reservoirs[J].Petroleum Exploration and Development，2005，32(5)：101-104.

[8] 单娴，姚军.基于渗透率张量的各向异性油藏两相渗流数值模拟[J].中国石油大学学报：自然科学版，2011，35(2)：101-106.SHAN Xian，YAO Jun.Numerical simulation for twophase flow in heterogeneous reservoirs based on full permeability tensor[J].Journal of China University of Petroleum(Edition of Natural Science)，2011，35(2)：101-106.

[9] BATYCKY R P.A three-dimensional two-phase field scale streamline simulator[D].California：Stanford University，1997.

[10] BERENBLYUM R，SHAPIRO A，JESSEN K，et al.Black oil streamline simulator with capillary effects[R].SPE 84037，2003.

[11] 王洪宝，苏振阁，陈忠云.油藏水驱开发三维流线模型[J].石油勘探与开发，2004，31(2)：99-103.WANG Hong-bao，SU Zhen-ge，CHEN Zhong-yun.A 3-D streamline model in waterflooding reservoir[J].Petroleum Exploration and Development，2004，31(2)：99-103.

[12] 李亚军，姚军，黄朝琴，等.考虑渗透率张量的非均质油藏有限元数值模拟方法[J].计算物理，2010，27(5)：692-698.LI Ya-jun，YAO Jun，HUANG Zhao-qin，et al.Finite element simulation of heterogeneous reservoir with full permeability tensor[J].Chinese Journal of Computational Physics，2010，27(5)：692-698.

[13] BAGHERI M，SETTARI A.Methods for modelling full tensor permeability in reservoir simulators[J].Journal of Canadian Petroleum Technology，2007，46(3)：31-38.

[14] LEUNG W F.A tensor model for anisotropic and heterogeneous reservoirs with variable directional permeabilities[R].SPE 15134，1986.

[15] 刘月田，徐明旺，彭道贵，等.各向异性渗透率油藏数值模拟[J].计算物理，2007(3)：296-300.LIU Yue-tian，XU Ming-wang，PENG Dao-gui，et al.Numerical simulation of petroleum reservoir with anisotropic permeability[J].Chinese Journal of Computational Physics，2007(3)：296-300.

[16] POLLOCK D W.Semianalytical computation of path lines for finite-difference models[J].Ground Water，1988，26(6)：743-750.

[17] FANCHI J R.Directional permeability[J].SPE Reservoir Evaluation&Engineering，2008(6)：565-568.