空间谱估计中误差自校正方法研究

黄传禄 晁 坤 毛云志

(中国电波传播研究所 青岛 266107)

空间谱估计中误差自校正方法研究

黄传禄*晁 坤 毛云志

(中国电波传播研究所 青岛 266107)

阵列误差一直是空间谱估计理论实际应用的一个主要瓶颈。该文提出了一种新的阵列误差自校正方法，结合有源校正与在线自校正理论和方法，通过利用一个空间位置方位不需要精确可知的辅助信号源，利用优化算法完成信号源角度以及阵列复增益误差的联合估计，然后将估计的阵列误差参数应用到其后的空间谱估计中。这种自校正算法具有准确度高的优点，并且属于离线算法，一方面避免了传统的有源校正方法对辅助源位置方位精度的严格要求，同时避免了在线自校正算法的大计算量，可以应用到实际空间谱估计中。

阵列信号处理；空间谱估计；阵列误差；误差自校正；参数优化算法

1 引言

空间谱估计是阵列信号处理的主要内容之一，其主要是指空间信号的波达方向估计，即 DOA (Direction of Arrival)估计。空间谱估计方法是信号处理领域的一个研究热点，在电子侦察、智能天线、雷达、声呐等领域具有广泛应用[1－6]。现代空间谱估计的主要算法有基于线性预测的最大熵算法(Maximum Entropy Methods, MEM)，基于子空间分解类的多重信号分类算法(MUltiple SIgnal Classification, MUSIC)，基于子空间拟合类的最大似然算法(Maximum Likelihood, ML)等[1,2]。通常的DOA估计算法是基于理想模型的，但在工程应用场合中各种各样的误差不可避免。当实际模型与假设模型不相符或者偏差较大时，许多基于理想模型的DOA算法的性能将严重下降，甚至失效。因此必须采取补偿或者误差校正措施。实际工程中误差来源主要有3类：一是有限数据长度快拍；二是不能先验已知或精确估计噪声协方差矩阵；三是导向矢量或阵列流型存在误差[1,7,8]。如何消除这些误差的影响，使DOA算法在应用中具有较强的稳健性，是DOA算法实用化的一个关键环节。当前处理模型未知或者存在误差时的DOA问题有两种手段：一种是有源校正方法；另一种有效的方法是进行自校正技术，即直接利用阵列采样数据进行信源方位估计的同时进行阵列误差参数的估计和校正[9－11]。

有源校正方法利用空间位置方位精确可知的辅助信号源，对阵列扰动参数进行离线估计，由于其无需对信号源方位进行估计，所以运算量较小，处理简单，在实用中应用较多。但有源校正对辅助信号源的方位信息精度要求高，如果不满足或者精度不够，则容易造成较大偏差[1,2]。自校正算法不需要辅助信号源，而是通过优化算法，实时完成信号源角度和阵列误差参数的联合估计，所以其校正精度比较高。但参数联合估计往往对应高维、多模非线性优化问题，这带来了算法复杂，运算量大的缺点，限制了其实用性[1,10]。因此，研究估计准确、算法简单、实用性强的阵列误差校正方法是空间谱估计理论实用化中的主要问题。

本文结合上面两种校正方法的优点，提出了一种新的误差校正方法。利用一方位信息不需要精确可知的辅助信号源进行误差自校正。即首先利用一辅助信号源进行信号角度和阵列误差参数的联合估计，将估计得到的误差参数应用到其后的空间谱估计中。从本质上，这是一种误差自校正算法，所以其对辅助信号源的空间位置信息没有要求。另外参数的联合估计计算是在空间谱估计之前的离线计算过程，并不影响空间谱估计时的计算速度。这可以简化阵列误差的校正过程，便于实际系统的使用。

2 阵列误差自校正算法

2.1 阵列误差模型

本文主要讨论阵列流型误差，其主要由通道特性不一致造成。阵列误差的影响主要体现在对阵列流型矩阵的扰动上，图1是包含通道误差的阵列接收模型，包含误差扰动的阵列接收信号为[1]：

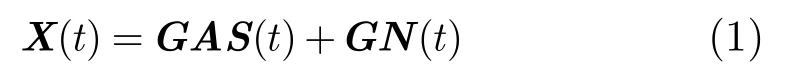
其中X(t)为阵列接收数据向量；A为理想阵列流型矩阵， A=[a(θ1),a(θ2),… ,a(θN)], a(θi)为对应于入射角的导向矢量；S(t)为入射信号向量；Ni(t)为空间时间平稳的噪声向量，满足 N分布，为噪声平均功率。G为阵列通道误差扰动矩阵，即如下的复增益扰动矩阵，主要包含通道增益误差和相位误差。

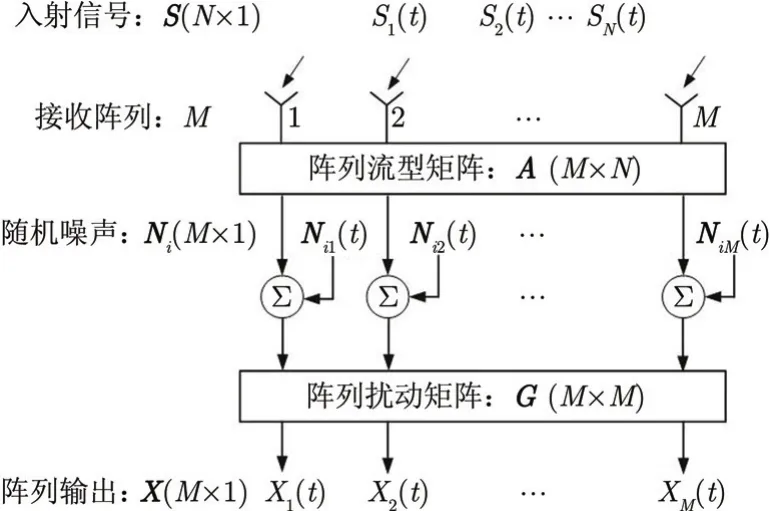
图1 阵列接收模型示意图Fig. 1 Schematic plan of array receive mode

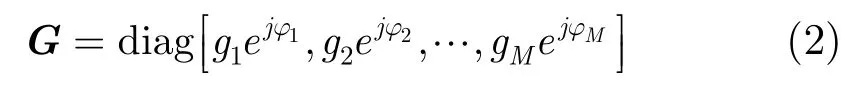
其中gi为增益误差，ϕi为相位误差。

阵列接收的协方差矩阵为：

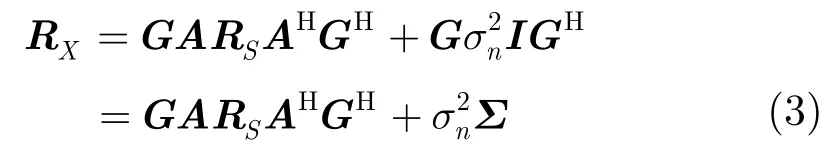
为分析简便，假设Σ=I。

2.2 DOA与增益联合估计算法

由经典MUSIC算法，式(1)描述的阵列模型的零谱函数可以写成[7]

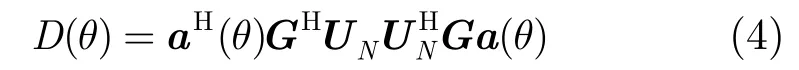
其中UN为由小特征值对应的特征向量构成的噪声子空间。信源角度和阵列误差参数的联合估计问题，即角度θ与G的联合优化问题：

由式(7)-式(9)，采用迭代法逐步估计角度θ和G，一直达到J收敛，便可以联合估计出信号角度和误差扰动矩阵。该自校正算法对阵列误差中的增益估计较准确，但对相位估计不够准确，尤其对均匀线阵，由于其导向矢量的范德蒙特性，算法的方位估计和相位估计存在模糊性[10]。

2.3 线性阵的角度和相位误差的联合估计

由式(3)可以看出，阵列接收数据的协方差矩阵的对角元素只包含信号和噪声的功率信号，而相位信息则包含在矩阵的非对角元素中。因此可以利用该特性，通过协方差矩阵的非对角元素来完成阵列相位误差的估计。

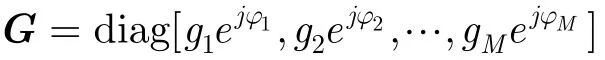
这样通过求解矩阵方程式(15)，就可以得到ϕ的估计值。但由于F不是列满秩，即 FHF是奇异的，导致方程式(15)没有唯一解。因此加上约束条件，ϕ在观察期间保持不变并且其均值为0，即[2]：

其中 H=(1 /(M -1))[ 1,1,… , 1]T。利用最小二乘法，可以得到式(18)的解为：

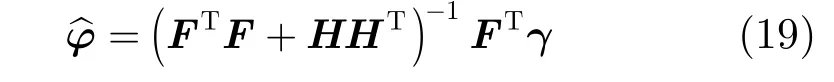
这样便可以求得阵列相位误差的估计值，其估计偏差的均值为：

其中Sϕ为相位扰动的和。从式(20)看出，阵元数目越大，其估计偏差越小，同时还可以看出，对前面通道的相位估计要比后面通道偏差更小。

2.4 加辅助源的阵列误差自校正方法

首先利用一辅助信号源，对其空间位置和方位并不精确要求，然后进行信号角度和阵列误差的联合估计，其中增益误差参数的估计采用2.2节介绍的算法，相位误差参数估计则采用2.3节算法，从而得到阵列误差参数，即扰动矩阵G。然后就可以利用式(1)描述的模型利用MUSIC算法(式(4))进行DOA估计。由上文叙述可以看出，提供辅助信号源只是为了提前进行一次空间谱估计，在估计中进行辅助源角度和误差参数的联合估计，得到误差参数的估计值。这从本质上是自校正算法，因此并不需要辅助源的精确方位信息。另一方面，在信源角度和阵列误差参数的联合估计中，多维参数优化等复杂的运算成为离线计算过程，不影响其后的空间谱估计过程。

3 仿真验证

在仿真计算中，采用1维均匀等距线阵，阵元数M=6，阵元间距d=0.5λ。假设有3个信号源分别位于 -1 5°,0°,1 5°，信噪比为10 dB。图2给出了当阵列增益有扰动而相位没有扰动时，利用2.2节方法自校正算法得到的空间谱曲线。图2中不同曲线代表不同迭代次数时的校正结果，1代表没有校正，即扰动矩阵为单位矩阵，0代表理想校正。从图2中可以看出，算法在第8次迭代时便已经接近理想曲线，说明算法对增益幅度校正较准确。图3为阵列误差加入了相位扰动时的空间谱计算曲线。可以看出，加入相位扰动时，2.2节的自校正算法估计性能变差，收敛次数增多，而且最终收敛的空间谱和理想曲线具有角度差。这说明了2.2节的自校正算法对线阵的相位估计具有模糊性，不够准确。比较图2和图3还可以看出，阵列的相位扰动相比幅度扰动对谱估计算法影响更大，也更难校正。

表1列出了阵列误差幅度和相位扰动的具体值以及估计值。从表 1中得出，2.2节的算法对增益幅度误差估计较准确，校正较好，但对相位误差估计偏差很大，显示了该自校正算法的局限性。

图 4为信号入射角度为-15°,0°,15°时，利用2.3节相位误差估计方法计算的空间谱曲线，在仿真中只考虑了增益相位扰动，没有考虑增益幅度扰动，即假设增益幅度是理想的。从图4中可以看出，经过校正后的空间谱曲线和理想状态下曲线基本重合，校正效果良好。图 5是在信号入射角为-20°,-5°,1 8°，并且阵列存在增益幅度扰动和相位扰动时空间谱曲线。其中阵列增益幅度误差参数由2.2节算法估计，而相位误差参数由2.3节算法估计得到。从图5可以看出，校正后的曲线和理想状态曲线基本吻合，说明了阵列增益幅度误差和相位误差参数估计较准确，最终DOA估计准确，验证了本文方法的有效性。

从2.4节描述和仿真模拟看出，本文提出的阵列误差自校正方法，其增益幅度误差和相位误差需要分别估计得到。而且相位误差较幅度误差影响更大。因此，在实际操作中，需要先利用2.2节的联合估计算法幅度误差参数，然后再利用2.3节算法得出相位误差参数。不能颠倒次序，因为2.3节估计相位误差参数时，是假设没有幅度误差或者幅度误差参数已知，这样才能保证误差参数估计的准确性。

为验证阵列误差校正的性能，我们利用估计角度的方差与克拉美-罗界比较，来判断估计的性能。克拉美-罗界是一切空间谱估计算法估计方差的下限，对于1维均匀等距线阵，在阵元数M和快拍数L以及信噪比SNR情况下，克拉美-罗界为[1,2]：

利用本文提出的误差校正的方法，进行100次仿真，然后按式(22)计算角度估计方差

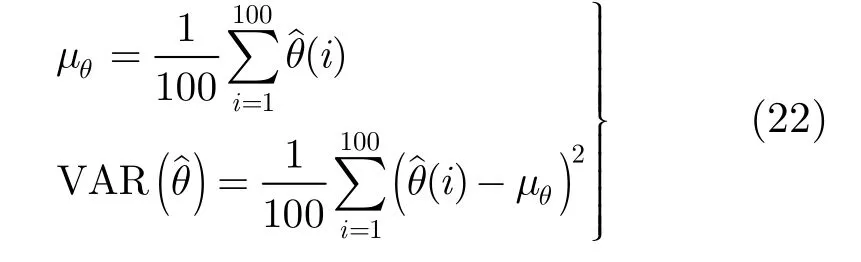
式(22)中角度以rad为单位。

图6给出了利用本文误差校正模型进行DOA估计的方差和空间谱估计克拉美-罗界(CRB)的曲线。如图所示，两者曲线基本一致，说明本文误差校正模型的准确性。从图6中可以看出，随着信噪比增高，估计的方差减少，而且与CRB越接近，说明校正效果更好。而随着信噪比降低，估计的方差增大，偏离CRB也更大，校正效果下降。图7为选取不同快拍数(式(10))时进行估计的方差。可以看出，当快拍数较小时，估计方差较大，与 CRB偏离也较大。这是因为当选取采样快拍数较小时，信号与噪声相关性增大，导致利用式(10)来估计协方差矩阵误差变大[1,12]。如图 7所示，当快拍数L＞ 100时，估计方差较小，与CRB偏差也较小，估计性能变好。

图2 增益幅度误差校正曲线图Fig. 2 The curve diagram of gain amplitude error calibration

图3 增益幅度和相位误差校正曲线Fig. 3 The curve diagram of gain amplitude and phase error calibration

表1 增益振幅和相位误差校正Tab. 1 The calibration of gain amplitude and phase errors

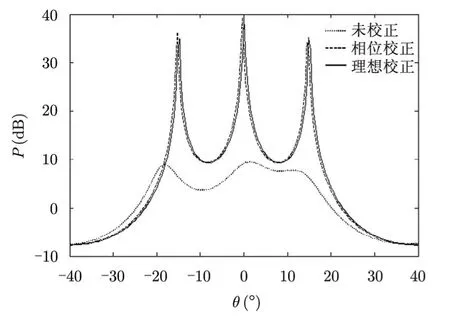
图4 相位误差校正曲线Fig. 4 The curve diagram of phase error calibration

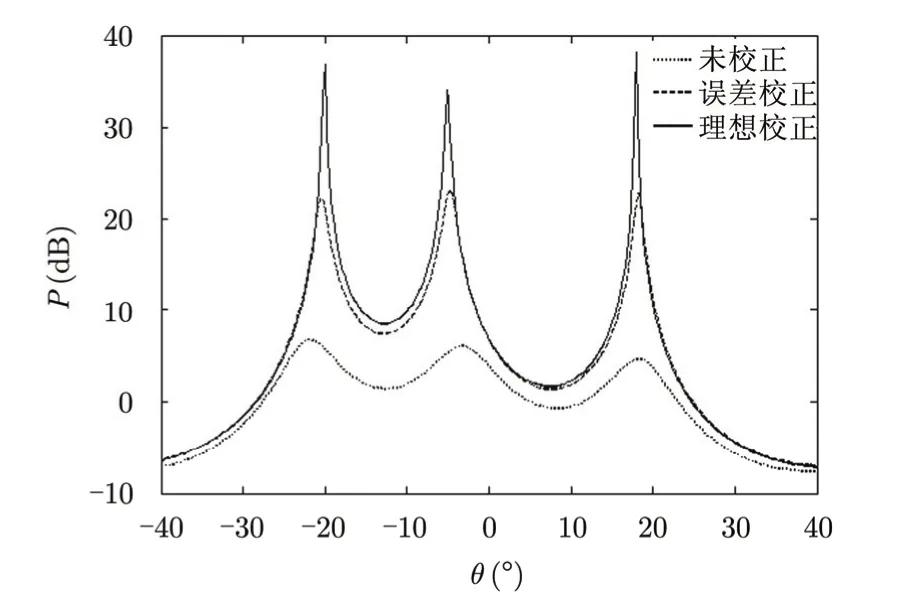
图5 增益和相位误差联合校正曲线Fig. 5 The curve diagram of gain amplitude and phase error jointing calibration

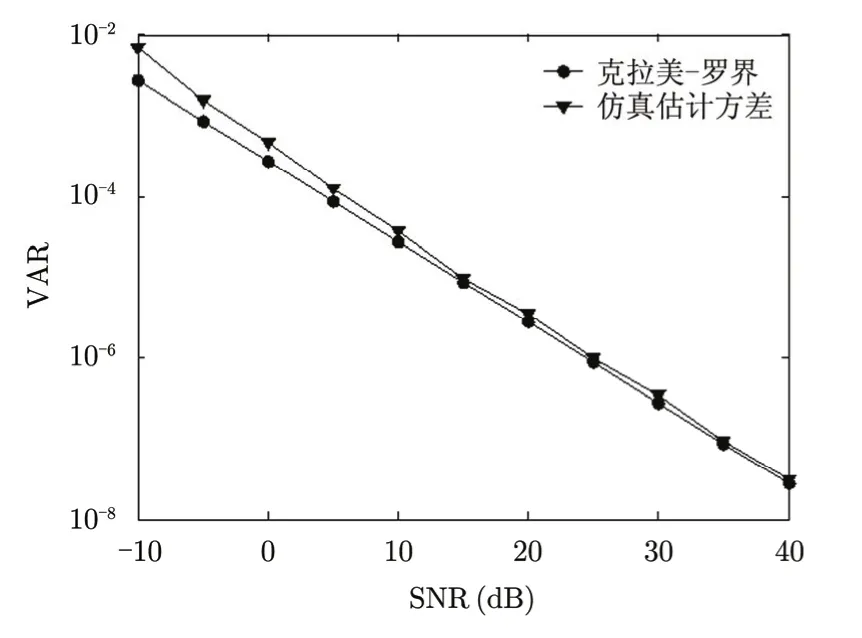
图6 估计方差随信噪比变化Fig. 6 The estimated variance vs. signal-to-noise ratio

图7 估计方差随快拍数变化Fig. 7 The estimated variance vs. snap number

4 结束语

本文提出了一种新的空间谱估计中阵列误差的校正方法。利用一辅助信号源进行预估计，同时得到阵列误差的增益幅度和相位误差参数的估计，从而在空间谱估计中进行阵列误差校正。这种方法避免了在线联合估计的庞大计算量，还避免了有源校正模型中对辅助源方位的高精度要求，可以在工程实际中应用。随着信噪比以及采样快拍数降低，估计的方差增大，校正效果下降，为保证估计性能，应选取较大的快拍数。本文方法为阵列误差校正提供了新的思路，具有理论及应用价值。但本文方法仅限于不依赖方位的阵列扰动及在估计周期内的慢不一致性。而对于阵元位置误差等角度依赖的相位扰动，以及估计周期内快不一致性的阵列误差校正[12]，尚需要进一步研究。

[1]王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 2-9.

Wang Yong-liang, Chen Hui, Peng Ying-ning, et al.. The Theory and Algorithms of Spatial Spectrum Estimation[M]. Beijing: Qinghua University Press, 2004: 2-9.

[2]刘德树, 罗景青, 张剑云. 空间谱估计及其应用[M]. 合肥: 中国科学技术大学出版社, 1997: 141-155.

Liu De-shu, Luo Jing-qing, and Zhang Jian-yun. The Technology and Application of Spatial Spectrum Estimation[M]. Hefei: University Press of Science and Technology of China, 1997: 141-155.

[3]孙逢林, 张升伟. 基于综合孔径辐射计稀疏阵列非均匀采样图像的快速重建[J]. 电子与信息学报, 2013, 35(4): 927-932.

Sun Feng-lin and Zhang Sheng-wei. Fast image reconstruction for non-uniform sampling of thinned array of synthesis aperture radiometer[J]. Journal of Electronics & Information Technology, 2013, 35(4): 927-932.

[4]齐子森, 郭英, 等. 柱面共性阵列天线盲极化波达方向估计算法[J]. 电波科学学报, 2011, 26(2): 245-252.

Qi Zi-sen, Guo Ying, et al.. Blind DOA estimation algorithm for cylindrical conformal array with respect to Polarization diversity[J]. Chinese Journal of Radio Science, 2011, 26(2): 245-252.

[5]王永良, 丁前军, 李荣峰. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009: 275-318.

Wang Yong-liang, Ding Qian-jun, and Li Rong-feng. Adaptive Array Processing[M]. Beijing: Qinghua University Press, 2009: 275-318.

[6]顾建峰. 阵列信号处理中若干问题研究[D]. [博士论文], 电子科技大学, 2008: 56-64.

Gu Jian-feng. Some researches on array signal processing[D]. [Ph.D. dissertation], University of Electron Technology, 2008: 56-64.

[7] Friedlander B and Weiss A J. Performance of directionfinding systems with sensor gain and phase uncertainties[J]. Circuits, System and Signal Processing, 1993, 12(1): 3-33.

[8]王鼎, 吴瑛. 基于旋转不变子空间均匀圆阵互耦自校正算法[J].电波科学学报, 2011, 26(2): 253-261.

Wang Ding and Wu Ying. Mutual coupling self-calibration algorithm for uniform circular array based on ESPRIT technique[J]. Chinese Journal of Radio Science, 2011, 26(2): 253-261.

[9] Friedlander B and Weiss A J. Direction finding in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(3): 273-283.

[10]Wylie M P, Roy S, and Messer H. Joint DOA estimation and phase calibration of linear equispaced (LES) arrays[J]. IEEE Transactions on Signal Processing, 1994, 42(12): 3449-3459.

[11]Flanagan B P. Self calibration of antenna arrays with large perturbation errors[D]. [Ph.D. dissertation], George Mason University, 2000: 47-61.

[12]Stavropoulos K and Manikas A. Array calibration in the presence of unknown sensor characteristics and mutual coupling[C]. Proceedings of the European Signal Processing Conference, Tampere, Finland, 2000, 3: 1417-1420.

黄传禄(1984-)，男，山东临沂人，2012年于中国科学院电子学研究所获得博士学位。现在中国电波传播研究所任工程师，主要从事微波技术、辐射探测、信号处理等工作。

E-mail: chuanlu01@163.com

晁 坤(1979-)，男，江苏徐州人，博士后，高级工程师，2008年博士毕业于西南交通大学电磁场与微波技术专业，现在中国电波传播研究所从事电磁理论、微波遥感、被动探测、太赫兹技术等方面的工作。

毛云志(1978-)，男，湖北武汉人，硕士，中国电波传播研究所工程师。目前主要研究方向为通信系统、数字信号处理。

Error Self-calibration Method in Spatial Spectrum Estimation

Huang Chuan-lu Chao Kun Mao Yun-zhi
(China Research Institute of Radiowave Propagation, Qingdao 266107, China)

An important bottleneck in spatial spectrum estimation theory is array errors. A new error self-calibration method is presented on the basis of active error calibration and online self-calibration theories. An algorithm combining Direction Of Arrival (DOA) estimation and array complex gain error calibration is developed using an auxiliary source without accurate spatial location information and numerical optimization calculation; the error calibration parameters can be used in the following spatial spectrum estimation. The method has a higher veracity than the active correction algorithm and is an offline calculation procedure, having the advantage of small computation amount, similar to the online self-calibration method, and avoiding accurate spatial location information in classical active calibration method.

Array signal processing; Spatial spectrum estimation; Array error; Error self-calibration; Parameter optimization algorithm

TN911

A

2095-283X(2014)05-0518-06

10.3724/SP.J.1300.2014.13147

2013-12-25收到，2014-04-14改回；2014-07-10网络优先出版国家部委基金资助课题

*通信作者： 黄传禄 chuanlu01@163.com