基于FRFT与Keystone变换的运动目标参数估计算法
田瑞琦 鲍庆龙 王丁禾 陈曾平
(国防科技大学自动目标识别重点实验室 长沙 410073)
基于FRFT与Keystone变换的运动目标参数估计算法
田瑞琦*鲍庆龙 王丁禾 陈曾平
(国防科技大学自动目标识别重点实验室 长沙 410073)
目标运动参数估计精度是衡量雷达探测系统性能的重要指标。该文为解决目标运动参数的估计问题,建立了运动目标回波模型,在利用分数阶傅里叶变换(FRFT)估计加速度的过程中采用数据融合提高估计精度,在估计出加速度的基础上通过Keystone变换和速度模糊通道解决距离走动(RCM)和多普勒模糊问题。仿真实验表明算法在估计精度和计算量上具有优势,并且对白噪声具有较好的鲁棒性。
分数阶傅里叶变换(FRFT);Keystone变换;参数估计;多普勒模糊
1 引言
在雷达探测系统中,回波相位特性[1]取决于目标相对雷达的运动关系。恒定的速度产生恒定的频移,恒定的加速度产生恒定的线性调频项。当目标相对于雷达做匀加速直线运动时目标回波为 LFM (Liner Frequency Modulation)信号,并且 LFM信号的参数与目标运动参数密切相关,因此可将目标运动参数估计问题转化为 LFM 信号的参数估计问题。
近些年来出现了多种利用时频分析对LFM信号参数进行估计的算法。例如,Wigner-Vile变换将原本的1维信号在2维时频平面上显示出来,文献[2]中指出LFM信号的Wigner-Vile分布为沿直线分布的冲激线谱,具有很好的时频凝聚性,但在处理多信号分量时,会出现分量间的交叉项问题,虽然通过核函数能够将其抑制,但LFM信号的时频凝聚性大大降低,严重影响参数估计精度。文献[3,4]联合Wigner-Vile分布和Hough变换对LFM信号的Wigner-Vile时频分布平面做直线积分,该算法虽然解决了交叉项问题,但因为Hough变换的引入使得算法的运算速度变慢,并且在计算过程中丢掉了信号的初始相位。文献[5]利用 FRFT (FRactional Fourier Transform)来估计目标运动参数,其实质为信号的时频分布在 FRFT域上的投影,该算法运算量远小于文献[3,4]的运算量,但FRFT无法估计目标初始距离,并且对于高速运动目标还存在着多普勒模糊问题。文献[6]采用Radon变换与 FRFT变换相结合的方法,避免了多普勒模糊问题的出现,并且在低信噪比的条件下能够很好地实现多个运动目标的检测与参数估计,但算法在实现过程中计算量较大,难以满足工程实现的实时性的要求。
本文提出一种联合FRFT与Keystone变换的方法估计目标运动参数。首先对目标回波做FRFT估计加速度,并在此过程中利用数据融合增强目标信号的能量凝聚性以提高估计精度。在加速度补偿之后的距离多普勒平面内分析了距离走动和多普勒模糊问题,通过 Keystone变换矫正距离走动,并对设定的多个模糊通道进行搜索解除多普勒模糊,从而估计出目标初始速度和初始距离,最后通过仿真实验验证算法的有效性。
2 基本原理
2.1 回波信号建模
假设目标相对雷达做匀加速直线运动,初始位移为R0,初始速度为v0,加速度为a,则接收到的基带回波信号为:
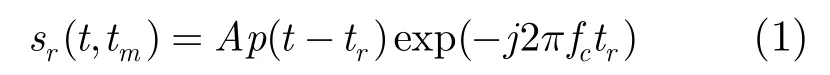
式中t代表快时间, tm=mTr代表慢时间,发射信号的表达式为 p(t)=rect(t/Tp),Tr为脉冲重复间隔,目标时延

可见,当雷达发射Chirp脉冲信号时,慢时间域目标回波为LFM信号,并且调频率为(2a)/λ,中心频率为(2v0)/λ。因此对目标运动参数的估计可以转化为对该LFM信号参数的估计。
2.2 分数阶傅里叶变换原理
信号x(t)的FRFT的定义为:

图1显示了LFM信号时频分布与FRFT变换的关系。在时频平面上,时间轴沿逆时针方向旋转π/2后便是频率轴。当p等于0时FRFT就是原信号,也就是信号在时间轴上的表示。p等于 1时FRFT则是原信号的傅里叶变换,也是信号在频率轴上的表示。当p从0变化到1时,信号平滑地从原始信号变化到傅里叶变换,因此信号的p阶FRFT可以认为是该信号在p阶分数阶傅里叶变换域中的表示,而p阶分数阶傅里叶变换域正是时频平面内时间轴逆时针方向旋转 α= (π/2)p 角度后得到的,见图1中的u轴。
2.3 Keystone变换原理
Keystone变换[7]能够较好地解决径向匀速直线运动目标在长时间积累过程中出现的跨距离单元走动问题,使得不同回波的能量在同一个距离单元内得到积累。
对式(1)在快时间域做傅里叶变换得到
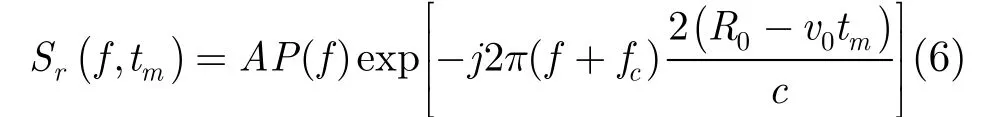
Keystone变换通过设定虚拟时间解快时间频域与慢时间域的耦合关系,虚拟时间τm= ((f+fc)/fc)tm,将其代入式(6)后乘以脉冲压缩函数得到
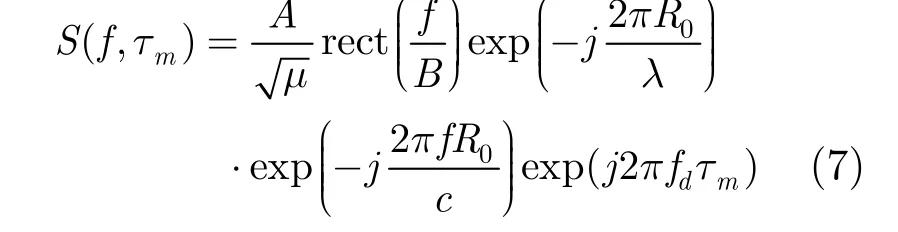
其中 fd=(2v0)/λ表示目标的多普勒频率,对式(7)做快时间域逆傅里叶变换得到
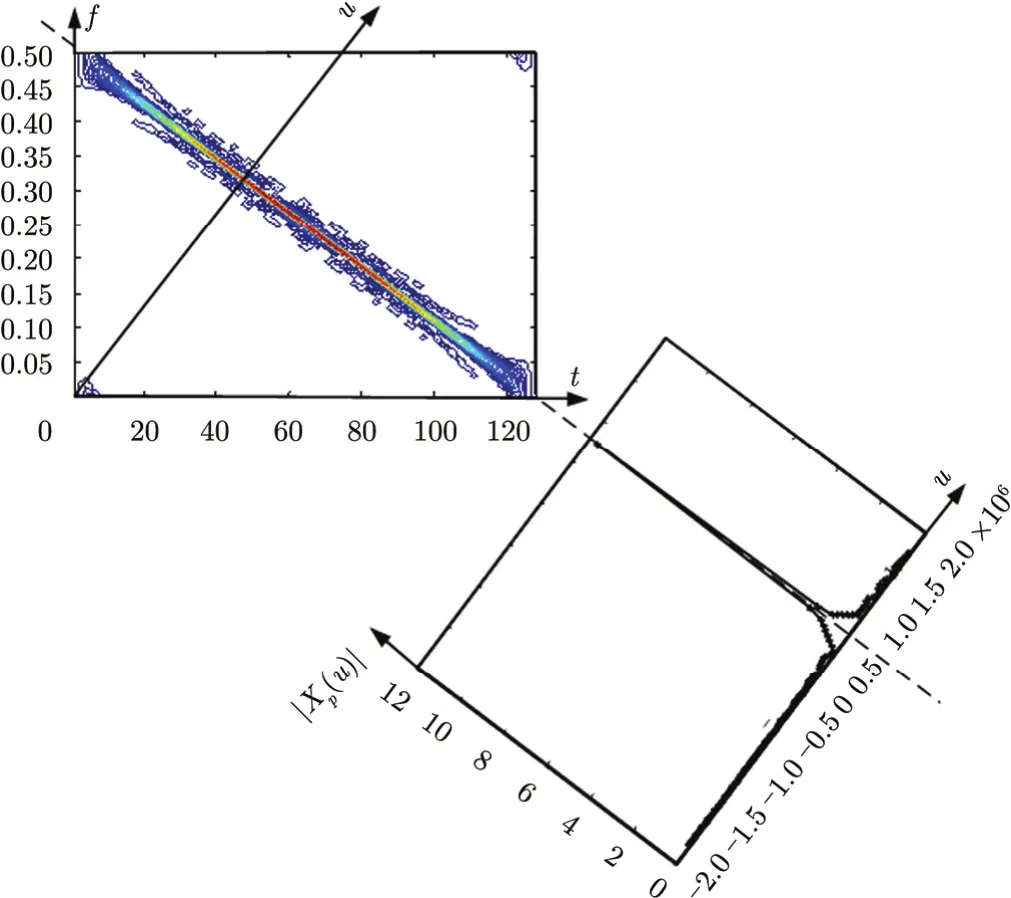
图1 LFM信号时频分布与FRFT变换的关系Fig. 1 Relationship of time frequency distribution and FRFT of LFM signal
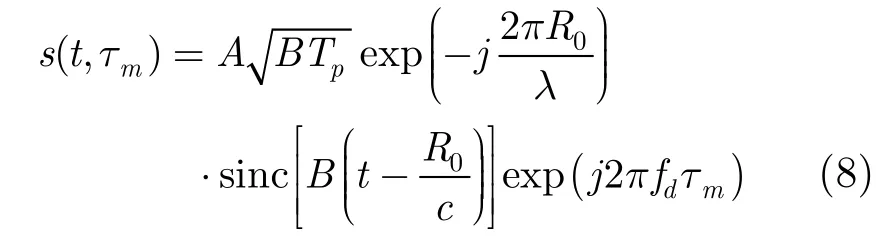
由式(8)可见,Keystone变换后脉冲压缩结果中不同回波的峰值对应时刻均为 tpeak=R0/c,这表明不同回波的能量集中在同一个距离单元内,因此距离走动得到补偿。
3 联合FRFT和Keystone变换的雷达信号处理方法
3.1 基于FRFT的目标加速度估计算法
LFM信号在时频平面上表现为背鳍形直线,如图1所示,直线与频率轴的交点表示初始频率f0,斜率为LFM信号的调频率u0。在某一特定的FRFT域上信号能量凝聚性最佳,又由于噪声的能量均匀分布于时频平面,不会出现能量凝聚现象。因此以旋转角度α为变量,以某一步长遍历一个角度周期后得到信号在不同u域上的表示,形成变量为α和u的2维参数空间,该参数空间内LFM信号的能量会在某一点处形成峰值,当峰值超过某一阈值证明回波中存在目标,设峰值点坐标为(α0,u0)。由图1中几何关系可知
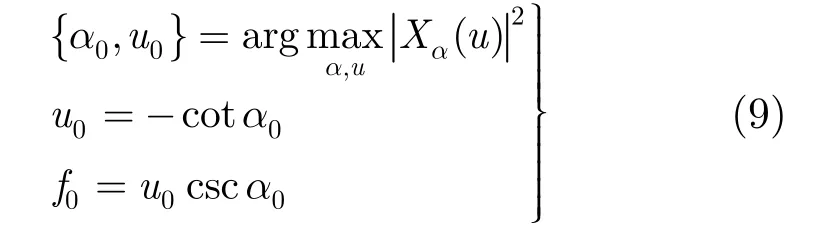
由式(2)和式(9)可知目标的加速度与LFM信号调频率的关系式为:

利用式(10)求解目标加速度时还应考虑信号处理过程中数据离散化问题。离散分数阶傅里叶变换的实现算法有很多,其中Ozaktas提出的分解型快速算法[8]被广为应用,该算法将FRFT分解为卷积的形式,其输出与连续FRFT的输出比较接近。在算法起初需要对离散数据进行量纲归一化处理,归一化处理分尺度变换方法和数据补零/截取法两种。本文选用尺度变化法来实现量纲归一化,这使得变换前后数据发生了畸变,因此在求得调频率和初始频率之后还需要利用尺度因子进行反变换才能得到真实的LFM信号参数。由尺度因子为S=,则目标真实加速度表达式为:
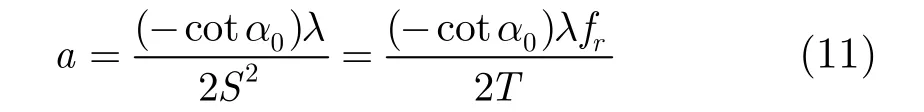
3.2 基于FRFT的数据融合与检测
当信噪比较低时即使回波中存在目标,单组慢时间域回波信号做 FRFT后其能量凝聚效果也达不到检测概率的要求,因此需要利用多组慢时间域信号进行数据融合,增强能量凝聚性,以提高检测概率。本文针对两种数据融合准则[9],根据本文特定的应用背景选择有效的数据融合方法。
单元选大准则是对多组FRFT 2维参数空间中每个单元进行选大处理,其表达式为:
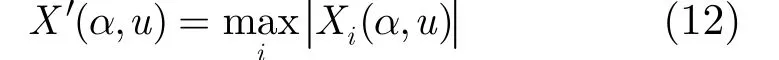
选大操作使得采样幅度损失小,但对噪声也做了选大处理,当回波信噪比较低时参数空间内没有明显的能量积累峰值,因此单元选大准则不适合本文的应用条件。
单元求和准则是对多个参数空间结果的叠加,其表达式为:
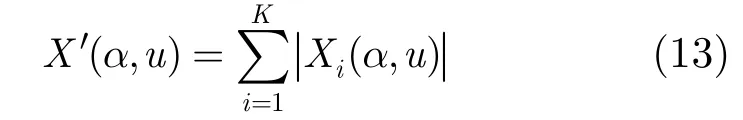
单元求和准则将各组数据中目标和噪声都叠加,但目标的相关性远大于噪声的相关性,噪声均匀分布于时频平面,目标则表现出凝聚性,因此叠加后信噪比较大。在本文应用背景下,各组数据中局部信噪比差异较小,因此选取单元求和准则来对多组慢时间域信号做数据融合处理。
3.3 基于Keystone变换的目标初始速度和初始距离估计算法
依照前两小节算法利用 FRFT估计目标加速度后对基带回波做2次相位补偿,补偿后的回波中只有1次相位,可将其看做匀速直线运动目标的回波。通过 Keystone变换补偿距离走动后在慢时间域做多普勒处理,由距离多普勒平面峰值便可求得目标初始速度和初始距离。当存在多普勒模糊时,同样可以实现距离补偿。假设模糊多普勒频率为fda,则目标真实的多普勒频率为:

k表示多普勒模糊数,最大模糊数根据目标的速度范围来设定。将式(14)代入式(7)中的多普勒指数项得
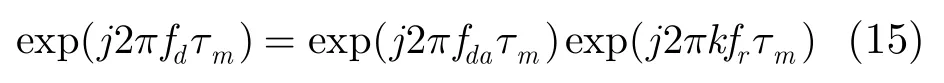
而式(7)中的fd实际上是模糊后的多普勒频率fda,因此对(7)需要乘以补偿因子exp(j2πkfrτm)后再分别对各模糊通道做慢时间域傅里叶变换,目标的多普勒模糊数与所有通道中最大峰值所在的多普勒通道号相对应,这样便可解除欠采样带来的多普勒模糊,并求得目标真实的多普勒频率。
根据第3节的描述可将本文运动目标参数估计算法的步骤概括如下:
(1) 提取N组慢时间域回波信号做FRFT得到N个2维参数空间,利用单元叠加融合准则对N个FRFT的2维参数空间做数据融合,增大目标回波的能量凝聚性。
(2) 若数据融合后2维参数空间中的峰值超过某一经验阈值T1便证明回波中存在目标,利用峰值处的坐标和式(11)便可以估计出目标的加速度aˆ。
(3) 利用估计出的加速度aˆ将原始基带回波中的2次相位项补偿掉,此时补偿后的回波可以看成是匀速直线运动目标的回波,对其做匹配滤波同时利用Keystone变换补偿距离走动。为解除多普勒模糊,在Keystone变换之前设定K个模糊通道,分别对每个通道的数据平面做匹配滤波和 Keystone变换。
(4) 将K个多普勒模糊通道分别做上述处理,再对慢时间维做FFT得到K个2次相位补偿后不同模糊通道的距离多普勒平面。K个平面中峰值最大处对应的多普勒通道号便是目标的多普勒模糊数,再根据该峰值坐标便可估计出目标的初始速度和初始距离。
本文算法信号处理流程图如图2所示。
4 仿真实验
4.1 数据融合与加速度估计实验
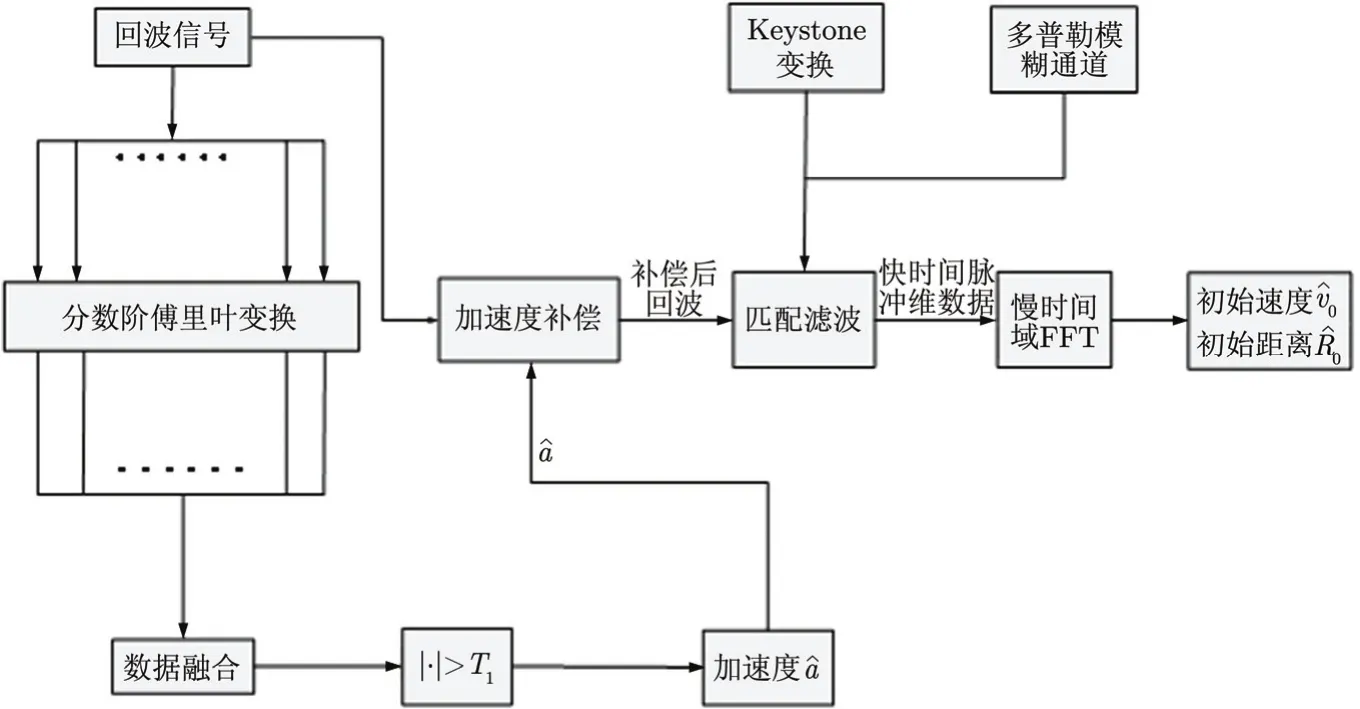
图2 本文算法信号处理流程图Fig. 2 Flow chart of proposed algorithm
系统参数设置如表1所示。数据融合前单组慢时间域回波的FRFT 2维参数空间如图3所示,30组回波数据融合后的参数空间如图 4。对比两幅图可以看出信噪比为-20 dB时,单组回波做 FRFT后目标能量凝聚性还不足以达到检测要求,但从多组回波数据融合的结果来看目标被突显出来,证明数据融合能增强目标回波的能量凝聚性。
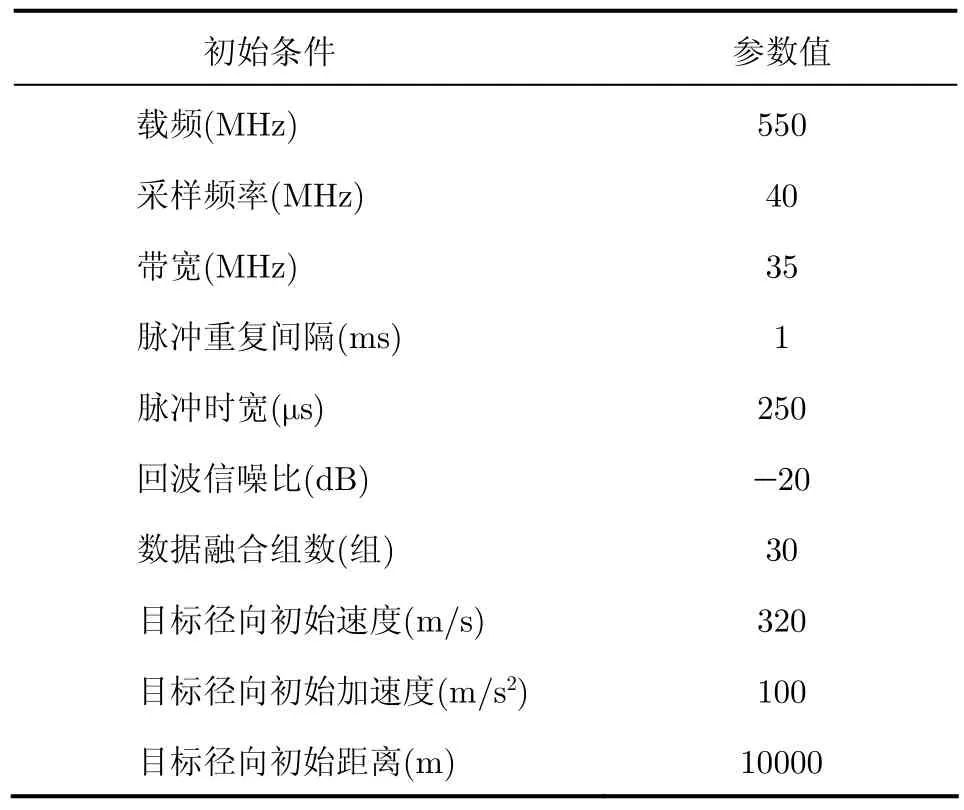
表1 系统参数设置Tab. 1 Set of system parameters
在不同信噪比条件下,经过1000次 Monte Carlo仿真实验,目标加速度估计的平均相对误差如表2所示。由表中数据可知,误差随信噪比的增大呈递减趋势,当信噪比高于-15 dB时,平均相对误差基本低于0.03,估计精度已达到较高水平,当信噪比高于5 dB时,加速度平均相对误差在一个很小的范围之内波动。可见FRFT在能量凝聚性方面具有突出优势,适用于低信噪比条件下的运动目标检测与参数估计。
4.2 初始速度和初始距离估计实验
按照表1中的目标参数设置,目标速度已超过无模糊速度v=(λfr)/4=136.3 m/s ,因此存在速度模糊。若在加速度补偿后不矫正距离走动直接做动目标检测(MTD)处理,其结果如图5所示。图6为加速度补偿之后利用 Keystone变换矫正距离走动并解除速度模糊后得到的最佳积累结果。图5中目标能量分散,并且由于速度模糊没有解除,无法根据多普勒频率估计出目标运动速度。图6中目标能量在某一个距离单元中得到积累,距离单元走动得以矫正,并且由于多普勒通道的设置解除了速度模糊,由此可准确估计出目标的真实初始速度。
4.3 不同参数估计算法的对比实验
文献[10]根据先验信息在一定范围内搜索加速度和速度,通过2次相位和1次相位补偿的方法估计目标参数。文献[11,12]利用Hough变换的思想将目标的直线航迹与参数空间中的点对应起来,从参数空间中点累加峰值反推目标运动参数。本节通过不同信噪比下的仿真实验来比较各算法参数估计精度。
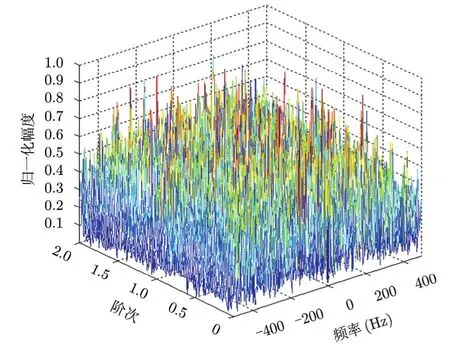
图3 数据融合前的FRFT 2维参数空间Fig. 3 Parameter space of FRFT before data fusion
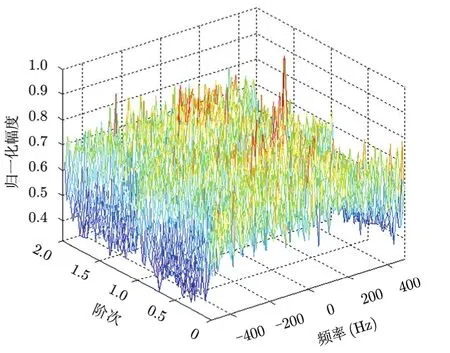
图4 数据融合后的FRFT 2维参数空间Fig. 4 Parameter space of FRFT after data fusion

表2 信噪比对参数估计精度的影响Tab. 2 Influence of SNB on parameter estimation
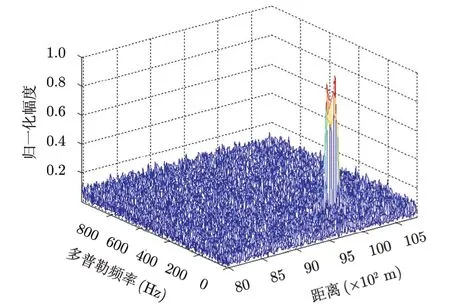
图5 加速度补偿后直接MTD积累结果Fig. 5 Accumulation result of MTD after acceleration compensation
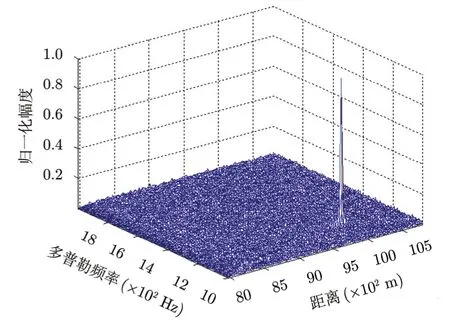
图6 本文算法积累结果Fig. 6 Accumulation result of the proposed method
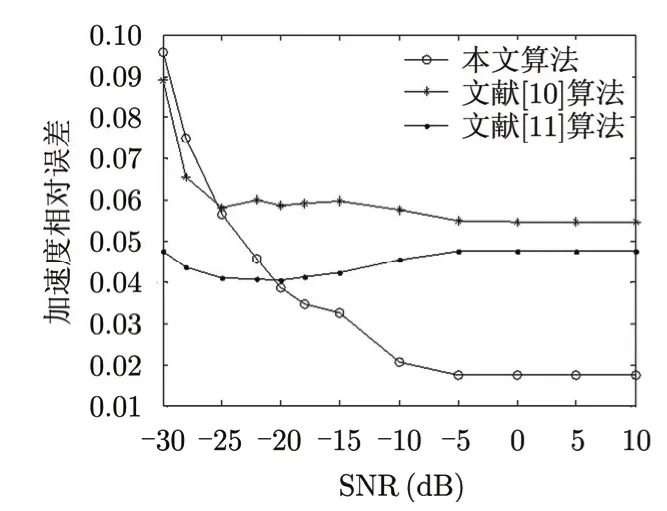
图7 加速度误差曲线Fig. 7 Error curve of acceleration
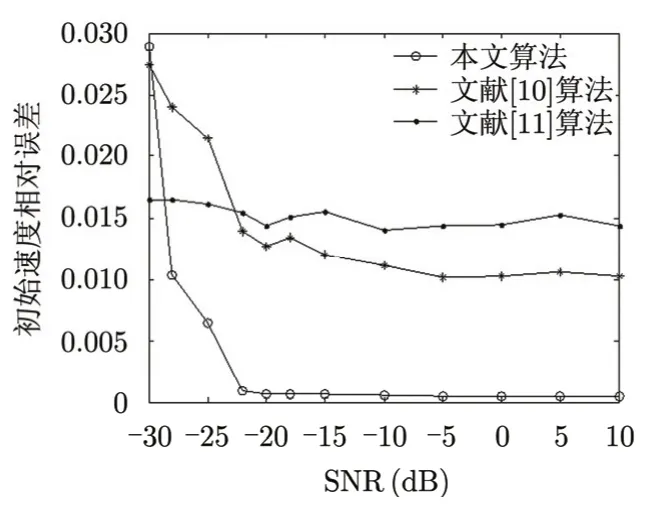
图8 速度误差曲线Fig. 8 Error curve of velocity
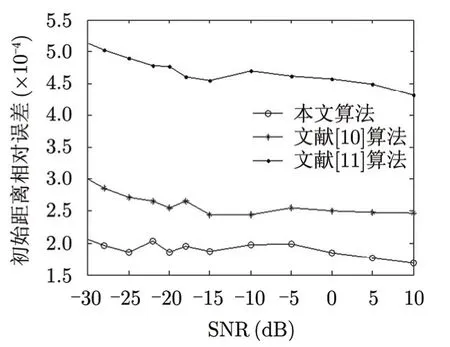
图9 距离误差曲线Fig. 9 Error curve of range
图7-图9为参数最小分辨单元相同的情况下,信噪比对参数估计精度的影响曲线。从图7和图8可见当信噪比高于-21 dB时,本文算法对加速度、初始速度的估计结果都优于文献[10]和文献[11]算法,并且本文算法和文献[10]算法的相对误差随信噪比的增大呈下降趋势,而文献[11]算法由于二元化处理使得算法本身对噪声不敏感,在信噪比观察区间内相对误差的波动很小。从图9可以看出3种算法对距离的估计误差都维持在一个相对较低的水平,信噪比的变化对距离估计误差的影响很小,并且本文算法误差最小。
从运算量上来分析,文献[10]算法需要在加速度和速度2维参数空间中搜索最佳补偿参数,在参数最小分辨单元相同的条件下,其运算量随搜索范围的增大而增大。在目标运动信息先验未知的情况下搜索参数范围较大,算法的运算量较大。同样,文献[11]算法在本文匀加速直线运动情况下搜索空间为3维,加上目标运动信息先验未知,使得算法运算复杂度显著增加。而本文算法只存在分数阶傅里叶变换中阶次p的1维搜索以及少数多普勒模糊通道的搜索,其运算量远小于上述两者。
5 结束语
本文为解决径向匀加速直线运动目标的参数估计问题,通过分数阶傅里叶变换估计目标的加速度,然后对 2次相位补偿后的回波数据利用 Keystone变换矫正距离走动,并设定多个模糊通道解除速度模糊,最终估计目标初始速度和距离。通过仿真实验,证明了本文算法在估计精度和运算量上的优势,并且对噪声具有较好的鲁棒性。
[1]陶然, 齐林, 王跃. 分数阶 Fourier的原理与应用[M]. 北京:清华大学出版社, 2004: 60-90.
Tao Ran, Qi Lin, and Wang Yue. Theory and Applications of the Fractional Fourier Transform[M]. Beijing: Tsinghua University Press, 2004: 60-90.
[2] Peleg S and Porat B. Linear FM signal parameter estimation from discrete-time observations[J]. IEEE Transactions on Aerospace and Electronics System, 1991, 27(4): 607-616.
[3]关欣, 仲利华, 胡东辉, 等. 一种基于RSPWVD-Hough变换的无源雷达多普勒展宽补偿方法[J]. 雷达学报, 2013, 2(4): 430-438.
Guan Xin, Zhong Li-hua, Hu Dong-hui, et al.. A compensation algorithm based on a RSPWVD-Hough Transform for Doppler expansion in passive radar[J]. Journal of Radars, 2013, 2(4): 430-438.
[4] Geroleo F G and Brandt-Pearce M. Detection and estimation of LFMCW radar signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 405-418.
[5] Guan Jian, Chen Xiao-long, Huang Yong, et al.. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter[J]. IET Radar, Sonar & Navigation, 2012, 6(5): 389-401.
[6] Chen Xiao-long, Guan Jian, Liu Ning-bo, et al.. Maneuvering target detection via radon-fractional Fourier transformbased long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939-953.
[7] Kirkland D. Imaging moving targets using the second-order keystone transform[J]. IET Radar, Sonar & Navigation, 2011, 5(8): 902-910.
[8] Ozaktas H M, Arikan O, Kutay M A, et al.. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9): 2141-2150.
[9] Nassar M O, Kanaan G, and Awad H A H. Framework for analysis and improvement of data-fusion algorithms[C]. IEEE International Conference on Management and Engineering, Chengdu, 2010: 379-382.
[10]Liu Xiao-bei, Fan Fang-fang, Cao Bao-long, et al.. Parameter estimation of LFM signal based on CAPON and Onedimensional Dechirp[C]. IEEE Conference on TENCON, Xi’an, 2013: 1-4.
[11]Moqiseh A and Nayebi M M. Combinational Hough transform for surveillance radar target detection in a 3-D data map[C]. IEEE Radar Conference, Rome, 2008: 9-12.
[12]Carlson B, Evans E, and Wilson S L. Search radar detection and track with the Hough transform, Part Ⅲ: detection performance with binary integration[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 116-125.

田瑞琦(1990-),女,湖南常德人,现为国防科学技术大学电子科学与工程学院硕士生,主要从事雷达信号处理等方面的研究。
E-mail: tianruiqi050804@126.com
鲍庆龙(1981-),男,吉林梅河口人,国防科学技术大学电子科学与工程学院讲师,主要从事雷达信号处理方面的研究。
E-mail: cbpest@163.com
王丁禾(1989-),男,山东枣庄人,国防科学技术大学电子科学与工程学院博士生,主要从事雷达信号处理方面的研究。
E-mail: wdhtsh81@163.com

陈曾平(1967-),男,福建福清人,教授,博士,博士生导师,国家 863专家组专家,国防科技大学电子科学与工程学院 ATR国防科技重点实验室副主任,主要从事雷达信号处理、自动目标识别等方面的研究。
E-mail: atrchen@sina.com
An Algorithm for Target Parameter Estimation Based on Fractional Fourier and Keystone Transforms
Tian Rui-qi Bao Qing-long Wang Ding-he Chen Zeng-ping
(ATR Key Laboratory National University of Defense Technology, Changsha 410073, China)
An important standard to measure the effectiveness of radar acquisition systems is the accuracy of target parameter estimation. To solve the estimation problem, the echo model of moving targets is established and the FRactional Fourier Transform (FRFT) is subsequently used to estimate the acceleration; further, data fusion is used to raise estimation accuracy. Finally, Range Cell Migration (RCM) and Doppler ambiguity are solved by using the Keystone transform and the ambiguity channels based on the estimated acceleration. The simulation results show high accuracy, complexity, and noise robustness.
FRactional Fourier Transform (FRFT); Keystone transform; Parameter estimation; Doppler ambiguity
TN957
A
2095-283X(2014)05-0511-07
10.3724/SP.J.1300.2014.14058
2014-03-27收到,2014-07-10改回;2014-09-05网络优先出版国家自然科学基金青年科学基金项目(81401489)资助课题
*通信作者: 田瑞琦 tianruiqi050804@126.com

