噪声条件下雷达关联成像误差分析
戴 强 程永强 秦玉亮 王宏强 黎 湘
(国防科技大学电子科学与工程学院 长沙 410073)
噪声条件下雷达关联成像误差分析
戴 强*程永强 秦玉亮 王宏强 黎 湘
(国防科技大学电子科学与工程学院 长沙 410073)
雷达关联成像是一种新的凝视高分辨率成像方法。该文针对参数化关联成像方法,建立了噪声条件下雷达关联成像模型,推导了噪声条件下关联成像理论误差限,分析了估计误差的影响因素。采用稀疏重构算法对不同参数条件下的雷达关联成像进行数值模拟,讨论了噪声条件下信号带宽、阵列构型、成像单元尺寸以及目标复杂度对成像误差的影响。研究结果为雷达关联成像系统的参数选取和信噪比要求提供了理论参考。
雷达关联成像;噪声;误差分析
1 引言
雷达高分辨成像经过数十年的发展,理论与技术已取得长足进步,部分成果已应用到武器系统中。尽管成像方法种类繁多,但通常都基于距离-多普勒原理,该原理对于非合作复杂运动目标存在明显缺陷,方位向分辨率取决于成像时间内目标相对雷达视线的转角,在“凝视/近凝视”的非理想观测几何条件下,分辨率难以保证;且高分辨成像需要时间积累,目标运动造成回波信号的非期望多普勒调制,运动补偿难度大。上述问题耗费了本领域诸多学者的大量精力,仍未得到根本解决,限制了成像与识别能力的大幅度提升。
雷达关联成像(radar coincidence imaging)是一种新的凝视高分辨率成像方法。通过对发射信号的波前调制,构造在时间和空间上具有随机分布的辐射场,通过关联处理实现对波束内目标信息的提取与解耦。由于辐射场的时空随机性,使得每次接收到的散射回波中含有相同的目标信息和不同的辐射场信息,利用关联处理技术进行信息的融合处理,可以获得超越天线孔径的空间分辨率。与传统SAR/ISAR雷达成像技术相比,雷达关联成像不依赖于雷达与目标的相对运动,可实现“凝视”成像,在全天时、全天候、高分辨对地观测系统、静止/准静止侦察平台凝视成像等领域具有重要应用价值。
近年来,国内多家单位相继开展了雷达关联成像技术研究,在随机辐射场的形成机理、随机辐射源构造、图像重构理论与方法、图像质量评估等方面取得了初步研究成果[1-6]。如文献[1]提出了基于时空随机辐射场的微波凝视成像方法,并进行了高分辨成像的初步探索,为深入研究雷达关联成像奠定了基础。文献[2]对微波雷达关联成像的成像过程和理论实现、数学模型建立、成像算法以及模型失配条件下的图像重构等问题进行了研究,提出了较为系统的雷达关联成像理论。文献[3]结合压缩感知(CS)思想,提出了稀疏目标的微波凝视关联成像信息处理方法。
雷达关联成像主要包括两种方法:相关成像法和参数化成像法。前者将接收信号与参考信号直接关联处理,对噪声不敏感,但是分辨率较低[1]。后者通过求解参数化成像方程获得目标散射系数的空间分布。该方法分辨率较高,但是对噪声敏感,低信噪比条件下成像误差较大。由于参数化方法求解过程复杂,目前尚无合适的方法描述其在噪声条件下的重构误差,所以本文采用理论推导和数值模拟验证的方法,研究了噪声对雷达关联成像误差的影响。
首先介绍了雷达关联成像数学模型;而后从参数估计的角度出发,推导了噪声条件下雷达关联成像的理论误差限,分析了估计误差的影响因素;采用稀疏重构算法对不同参数条件下的雷达关联成像进行数值模拟,讨论了噪声条件下,信号带宽、阵列构型、成像单元尺寸以及目标复杂度对成像误差的影响。研究结果为低信噪比条件下雷达关联成像系统参数的选取提供了理论参考。
2 雷达关联成像模型
雷达关联成像几何如图1所示。雷达采用多发单收结构,阵列含有N个发射阵元和1个接收天线。通过目标探测和跟踪技术,可得到目标中心位置的估计,并以此中心确定成像平面I的位置。在成像平面I的中心建立XY坐标系,记为成像坐标系。成像平面被划分为多个网格,称为成像单元,每一个成像单元近似由其中心的坐标表示,即成像单元到发射天线的距离近似为到中心的距离,该单元的散射特性记为其中心点处目标的散射系数。各阵元发射特定形式的随机信号Stn(t),在成像平面处形成2维随机辐射场。与目标发生作用后,回波信号Sr(t)由接收阵元接收并传送到信号处理端,与2维随机辐射场参考信号进行关联处理,求出各个成像单元的散射点强度,从而得到目标散射点的位置,最终得到目标重构图像[6]。
参数化方法利用辐射场参考信号和雷达回波的相互关系,建立起如下方程:


图1 雷达关联成像几何Fig. 1 Geometry of radar coincidence imaging
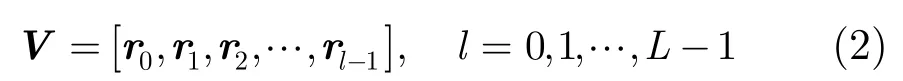
其中,lr为位置矢量,L为成像单元的数量。所有成像单元的参数系数组合为散射矢量:

其中,c为光速,Rn和Rr分别表示发射阵元和接收天线的位置矢量,N为阵元数量,可见参考信号是时间t和空间变量r的函数。因此,参考信号可以写成矩阵形式,则式(1)的具体形式为:

方程中各项与式(1)一一对应。显然,方程有唯一确定解的充分条件是SK×L为非奇异矩阵。因此,发射信号和接收信号的时间采样点个数不能少于成像单元的个数。可以看出,矩阵的秩由发射信号在时域上的不相关度和各个阵元信号的正交性决定的。在满秩的前提下,可以确定散射矢量为σ=。
对于静止目标,式(7)严格成立,采用直接求逆可以准确地求解出目标散射矢量σ,较好地重构目标图像。然而在实际场景中,复杂运动目标和噪声是普遍存在的,考虑到噪声、目标高速运动等引起的误差时,式(1)等式两边不再严格相等,直接求逆无法正确重构出目标的图像。稀疏重构算法利用了回波信号矢量的稀疏性,可对复杂条件下的目标实现高质量的图像重构[2],目标散射矢量表示为:
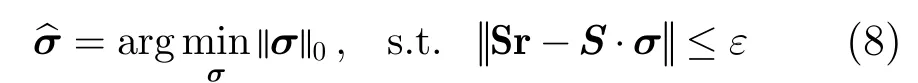
其中,ε为常数,是参数估计的约束条件。
3 噪声条件下成像误差影响因素分析
如上所述,在噪声存在的情况下,式(1)的方程不再成立,图像重构转变为一个参数估计问题,成像误差取决于对目标散射点参数估计的精度。包含测量噪声的关联成像方程如式(9)所示:
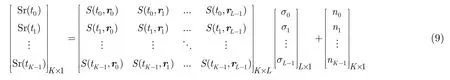
与式(7)相比,接收信号里增加了噪声分量。式(9)可以表示成式(10)所示的矢量形式:

其中,Sr为接收信号矢量,S表示参考信号矩阵,σ为目标散射系数矢量,n为测量噪声矢量。因此,关联成像转变为根据接收信号矢量Sr对目标散射矢量σ进行估计的问题。
关联成像误差与参数估计的精度有关,而参数估计精度可以由估计误差方差的下限,即 ˆ CRLB(σ)来描述。根据参数估计的基本结论[7],在高斯分布噪声条件下,估计误差方差的下限可以表示为:
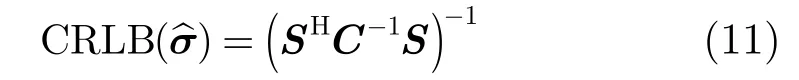
其中,H表示矩阵的共轭转置,C为噪声的协方差矩阵,则 C=σn2IK, IK为K维单位矩阵, σn2为噪声能量,则有:
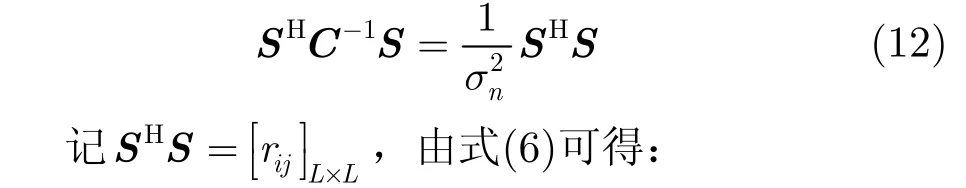

设 Rn(τ)为发射信号的自相关函数,发射信号是功率为 σs2,带宽为B的高斯随机信号,则其时域表达式为:
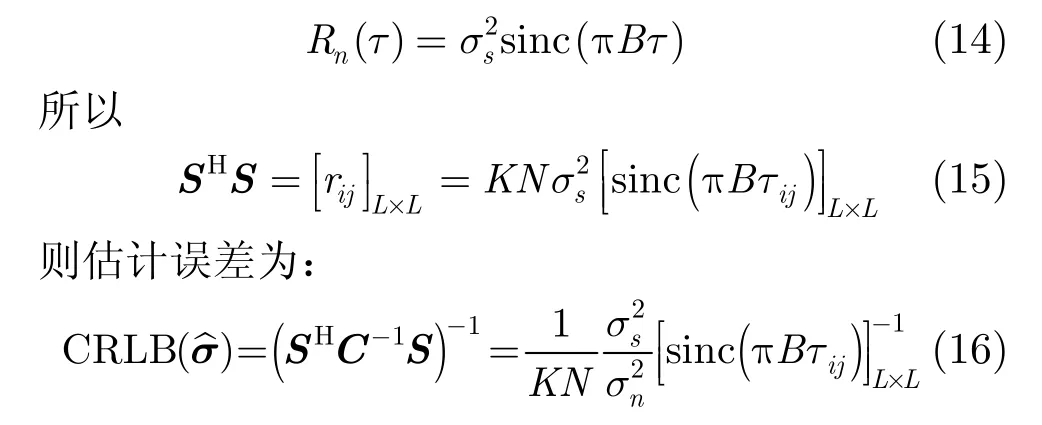
其中 σs2/σn2为发射信号与噪声的功率比,则接收信号的信噪比可表示为:
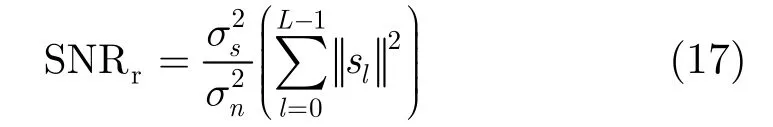
其中sl为目标的RCS。则总的估计误差方差的下限为:

根据式(18)可以分析得到,参数估计误差与接收信号的信噪比、发射信号带宽、目标散射点个数以及回波时延等因素有关。带宽和信噪比与估计误差成反比,带宽和信噪比越大,则估计误差越小;而阵列构型和成像单元的尺寸对回波时延都有影响,进而影响到估计误差。因此,在一定的信噪比条件下,改变发射信号带宽、阵列构型、网格尺寸和目标复杂度都会影响误差的估计精度。
4 仿真与结果分析
4.1 仿真实验方法
本节主要通过仿真实验来分析不同的参数条件和信噪比对参数化成像方法的成像误差的影响。设雷达的载波频率为 fc=9.5 G Hz ,带宽B=250 MHz,脉宽Tp=100 μ s;目标模型采用4个静止点目标的简单模型,散射点坐标分别为(-0.5,0.5), (0.5,0.5), (0.5, -0.5), (-0.5,-0.5);发射阵列含有8个均匀排列的阵元,阵元间隔0.2 m,阵列中心到成像平面中心的距离为1000 m,如图2所示。成像平面的面积设定为8 m×8 m,划分为16×16个网格,则每个网格的大小为0.5 m×0.5 m。
为了比较不同参数条件下噪声对成像误差的影响,分别改变上述实验参数中的带宽、阵列构型、网格尺寸和目标模型,然后将相应的接收回波数据Sr按信噪比大小不同加零均值高斯白噪声,其中信噪比的定义为:
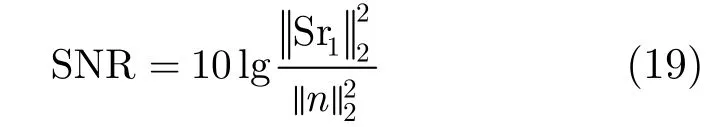

其中,δ越小则代表成像误差越小,反之亦然。
4.2 结果分析
采用基于cvx程序包的稀疏重构算法在上述参数条件下对目标进行成像,结果如图3所示。
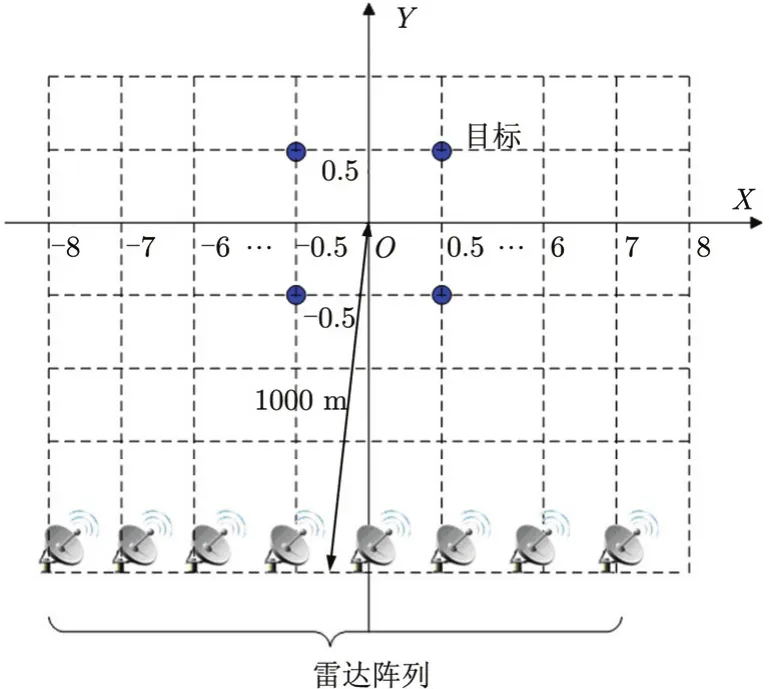
图2 目标与雷达几何示意图Fig. 2 Geometric diagram of target and radar
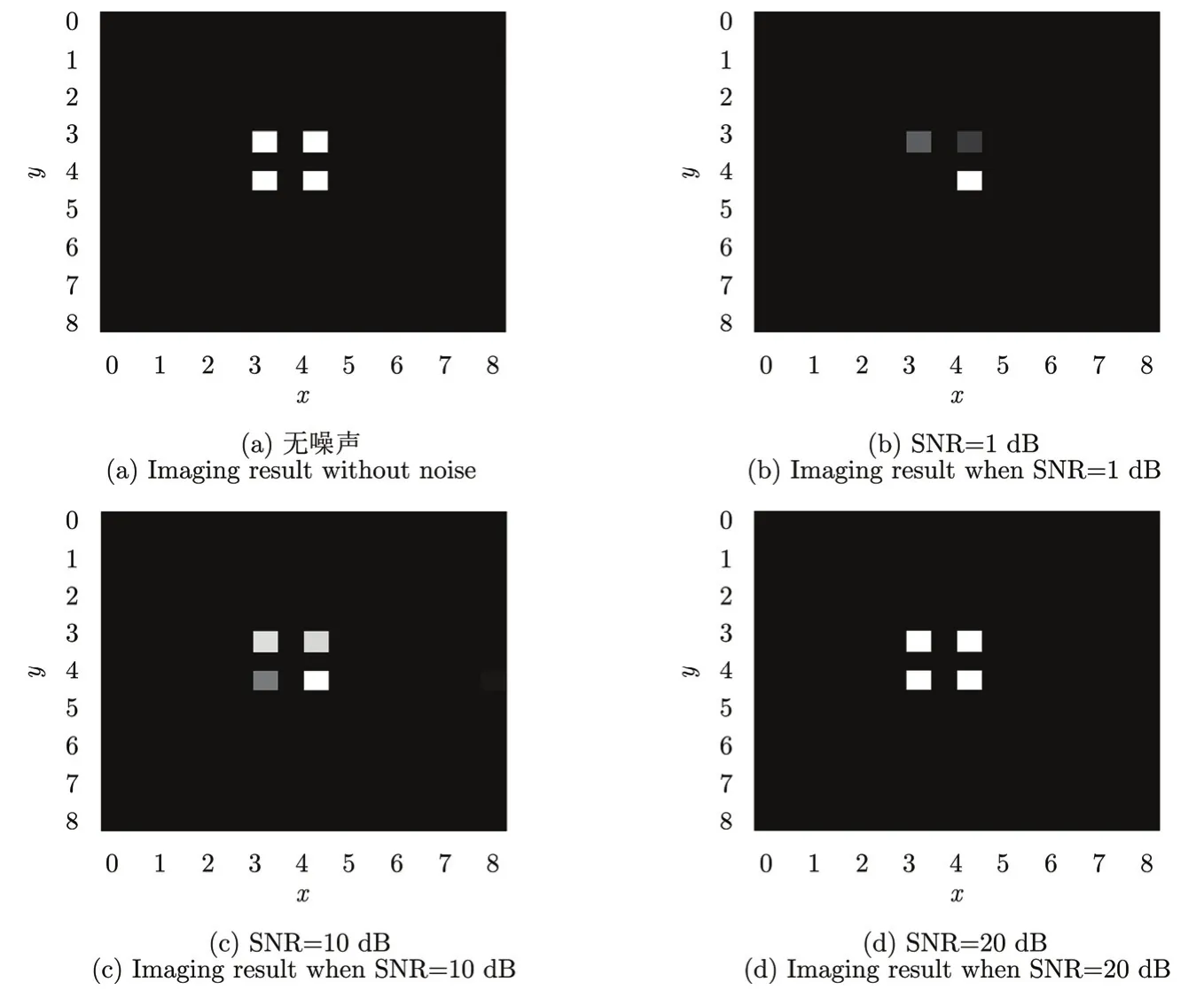
图3 4个点目标成像结果Fig. 3 Imaging result of four scatterers target
由图3可以看出,无噪条件下的成像结果准确地估计了目标散射点的位置和强度。当SNR=5 dB的时候,目标散射点出现强度不够和目标残缺的情况,当SNR=10 dB的时候,成像结果能准确估计散射点的位置,但是强度出现偏差。当SNR=20 dB的时候,重构图像的位置和散射点强度与真实值相比没有改变,可见高信噪比条件下成像误差较小。可见,噪声会对稀疏重构算法的成像误差产生影响。
下面仿真在信噪比1~20 dB的范围内,在上述参数的基础上改变发射信号带宽、阵列构型、网格大小和目标散射点个数等参数,利用稀疏重构算法得出在不同参数条件下的成像相对误差δ和CRLB随信噪比变化的曲线图。
图4给出了不同带宽的仿真结果。分别取带宽为250 MHz和500 MHz,其他参数不变。图4中“δ-250 MHz”和“δ-500 MHz”分别表示带宽为250 MHz和500 MHz的成像误差曲线,“CRLB-250 MHz”和“CRLB-500 MHz”分别表示带宽为250 MHz和500 MHz的CRLB曲线。可见,当信噪比相同时,带宽为500 MHz误差较小;成像误差相同时,带宽为250 MHz需要更高的信噪比。成像相对误差δ和CRLB曲线都很好地验证了这一点。因此,在相同的信号形式和信噪比条件下适当增加发射信号带宽可以减小成像误差。
图5给出了不同阵列构型的仿真结果,“δ-1行8列线阵”和“δ-2行4列面阵”分别表示阵列构型A和阵列构型B的成像误差曲线,“CRLB-1行8列线阵”和“CRLB-2行4列面阵”分别表示阵列构型A和阵列构型B时的CRLB曲线。可见,相同信噪比条件下,阵列构型A的成像误差和CRLB均小于阵列构型B,而在误差相同时,阵列构型B需要更高的信噪比。
图6给出了不同成像单元尺寸的仿真结果。分别取网格尺寸为0.5 m×0.5 m和0.25 m×0.25 m,网格数目不变,相应的成像平面尺寸为8 m×8 m和4 m×4 m,其他参数不变。图6中,“δ-网格0.5 m×0.5 m”和“δ-网格0.25 m×0.25 m”分别表示网格尺寸为0.5 m×0.5 m和0.25 m×0.25 m的成像误差曲线,“CRLB-网格0.5 m×0.5 m”和“CRLB-网格0.25 m×0.25 m”分别表示网格尺寸为0.5 m×0.5 m和0.25 m×0.25 m时的CRLB曲线。可见,在信噪比较低时,相同信噪比下前者的成像误差小于后者,而在信噪比较高时趋于一致。二者的CRLB曲线也较好了反映了这一特性。因此,在低信噪比条件下,网格尺寸为0.5 m×0.5 m的成像误差比0.25 m×0.25 m的成像误差小。
图7给出了不同目标复杂度的仿真结果。目标模型分别取4个点目标和12个点目标,其中4个点目标的模型同上,12个点目标的模型如图8(a)所示。图7中,“δ-4个点目标”和“δ-12个点目标”分别表示目标散射点个数为4和12时的成像误差曲线,“CRLB-4个点目标”和“CRLB-12个点目标”分别表示目标散射点个数为4和12时的CRLB曲线。可见,在信噪比相同时,4个点目标的成像相对误差小于12个点目标的成像相对误差,对应的CRLB也是如此。而当误差相同时,12个点目标要求更高的信噪比。
综合图4-图7的结果可以看出:(1)CRLB与成像相对误差δ随信噪比变化的趋势是一致的,为描述关联成像误差提供了理论限;(2)虽然 CRLB是无偏估计量误差方差下界,但稀疏重构等参数化方法求解结果大多是有偏估计量,其误差有可能小于CRLB。
选取的阵列构型如图8所示,阵列构型A为1行8列均匀排列的线阵,阵列构型B为2行4列均匀排列的面阵,阵元间距均为0.2 m,其他参数不变。

图4 不同带宽的误差曲线图Fig. 4 Error curves of different signal bandwidth
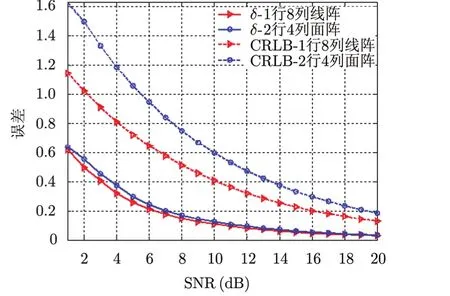
图5 不同阵列构型的误差曲线图Fig. 5 Error curves of different array configuration
图9给出了12个点目标成像结果。由图9可以看出,12个点目标的成像质量随着信噪比的提高而改善,但是在SNR=20 dB时成像结果与无噪声情况相比,散射点强度有所减弱。结合图3的结果可知,成像误差一定时,目标散射点数目越多,对信噪比要求越高。
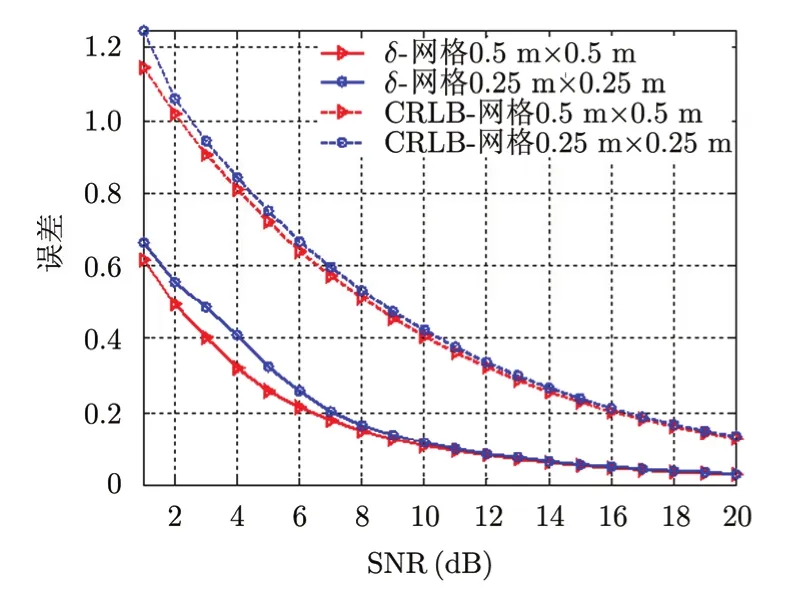
图6 不同成像单元尺寸的误差曲线图Fig. 6 Error curves of different size of imaging unit

图7 不同目标复杂度的误差曲线图Fig. 7 Error curves of different target complexity

图8 阵列构型Fig. 8 Array configuration

图9 12个点目标成像结果Fig. 9 Imaging result of twelve scatterers target
5 结论
本文针对实现雷达关联成像的参数化方法,分析了噪声条件下成像误差的影响因素,并通过数值模拟分析了信号带宽、阵列构型、网格尺寸和目标复杂度对成像误差的影响,这对即将实现的雷达关联成像系统在实际噪声环境中如何选择合适的参数以提高成像质量,具有一定的指导意义。此外,由于参数化方法对噪声的敏感性,低信噪比条件下关联成像算法是需要进一步研究的问题。
[1] 周海飞. 基于时空随机辐射场的微波凝视新方法及其辐射源特性研究[D]. [硕士论文], 中国科学技术大学, 2011.
Zhou Hai-fei. Research of a new microwave staring method based on time-space random radiation and its characteristics of radiation source[D]. [Master dissertation], University of Science and Technology of China, 2011.
[2] 李东泽. 雷达关联成像技术研究[D]. [博士论文], 国防科学技术大学, 2014.
Li Dong-ze. Research of radar coincidence imaging[D]. [Ph.D. dissertation], National Uinversity of Defense Technology, 2014.
[3] 何学智. 微波凝视关联成像的信息处理方法与仿真[D]. [博士论文], 中国科学技术大学, 2013.
He Xue-zhi. Information processing and simulation of microwave staringt and relating imaging[D]. [Ph.D. dissertation], University of Science and Technology of China, 2013.
[4] 陈建平, 朱文贵. 一种微波关联成像的新方法[J]. 海军航空工程学院学报, 2012, 27(2): 196-198.
Chen Jian-ping and Zhu Wen-gui. A new method of microwave relating imaging[J]. Journal of Naval Aeronautical Engineering Institute, 2012, 27(2): 196-198.
[5] Li Dong-ze, Li Xiang, Cheng Yong-qiang, et al.. Three dimensional radar coincidence imaging[J]. Progress In Electromagnetics Research, 2013, 33: 223-238.
[6] Li Dong-ze, Li Xiang, Qin Yu-liang, et al.. Radar coincidence imaging: an instantaneous imaging technique with stochastic signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 2261-2277.
[7] Kay S M. Fundamentals of Statistical Signal Processing: Volume I: Estimation Theory[M]. New Jersey, USA: Prentice Hall PTR, 1993.
Error Analysis of Radar Coincidence Imaging in the Presence of Noise
Dai Qiang Cheng Yong-qiang Qin Yu-liang Wang Hong-qiang Li Xiang
(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Radar coincidence imaging is a new method for high-resolution staring imaging. First, the mathematical model is constructed. Second, the theoretical error for radar coincidence imaging in the presence of noise is derived using the parametric imaging method. Third, the factors that affect the error are analyzed. Fourth, the sparse reconstruction algorithm is used to perform numerical simulations of radar coincidence imaging with different parameters. Finally, the effects of signal bandwidth, array configuration, size of the imaging unit, and target complexity on image error in the presence of noise are discussed. This study provides the theoretical framework for parameters selection and SNR requirements for radar coincidence imaging systems.
Radar coincidence imaging; Noise; Error analysis
TN957
A
2095-283X(2014)05-0541-07
10.3724/SP.J.1300.2014.14029
2014-02-18收到,2014-03-11改回;2014-08-25网络优先出版国家自然科学基金(61302149, 61101182)资助课题
*通信作者:戴强 303101282@qq.com
戴 强(1986-),男,国防科技大学硕士生,研究方向为雷达关联成像等。
程永强(1982-),男,国防科技大学讲师,研究方向为统计信号处理和信息几何等。
秦玉亮(1980-),男,国防科技大学副研究员,研究方向为SAR成像、雷达信号处理等。

