基于延迟共轭相乘的弹道目标平动补偿
贺思三 赵会宁 张永顺
(空军工程大学防空反导学院 西安 710051)
基于延迟共轭相乘的弹道目标平动补偿
贺思三*赵会宁 张永顺
(空军工程大学防空反导学院 西安 710051)
弹道目标微动叠加在弹道高速平动基础上,为了获得目标的微多普勒信息,需要对平动进行补偿。该文提出了一种基于延迟共轭相乘的平动参数估计方法,该方法通过延迟共轭相乘保留平动信息而消除微动的影响,并将平动参数估计问题转换为多项式相位信号参数估计问题,实现了平动参数的估计。仿真结果表明,所提算法能够在较低信噪比下实现平动参数的高精度补偿。
弹道目标;微多普勒;平动补偿;延迟共轭相乘
1 引言
基于微多普勒信息的弹道目标特征提取及识别技术是当前研究热点。大量文献对弹道目标微多普勒建模、微多普勒信息获取及微动参数估计展开了研究。对弹道目标而言,微动是叠加在目标沿弹道高速平动的基础上,平动分量的存在将使得回波信号的多普勒信息既包含了平动多普勒信息又包含了微多普勒信息,在对微动参数提取之前,需要对弹道目标高速平动进行补偿。
针对匀加速平动目标,航天二院的高红卫等人分析了目标速度[1]和加速度[2]对微多普勒信息的影响,并提出利用多普勒中心法对平动速度进行补偿[1],利用频谱重排的方法对加速度进行补偿[2];文献[3]则利用Hough变换对匀加速目标的平动信息进行补偿;文献[4]根据谱熵最大准则对加速度进行补偿。上述方法均基于目标匀加速平动假设前提,为了对更为复杂的运动目标进行平动补偿,空军工程大学的杨有春等人对基于强散射中心多普勒信息的平动补偿进行了研究,先后提出了一种基于多普勒极值点信息的平动补偿方法[5]和一种基于最强散射点多普勒信息的平动补偿方法[6];文献[7]利用经验模式分解技术对距离像序列中强散射中心的位置信息进行分解,认为分解后的余量对应了目标平动信息,从而对平动进行补偿。文献[5-7]所对应方法均是基于强散射中心信息的,要求散射中心一致且连续可见,当信噪比降低或目标部件遮挡导致散射中心在某些时间段缺失时将失效。考虑到共轭相乘可以降低多项式相位(对应为平动)的阶数,而具有正弦变化形式的微多普勒信号在共轭相乘后是幅度进行变化了的正弦信号,文献[8]和文献[9]通过对回波信号的共轭相乘消除平动的影响,从而保留幅度缩放后的微多普勒信息。但该方法在目标包含多个散射中心时变换后信号会出现散射中心之间的交叉项,影响进一步的微动特征提取精度,且该方法仅适用于正弦变化的微多普勒信号。
受文献[8],文献[9]启发,本文提出了一种基于延迟共轭相乘的平动参数估计方法。文献[8],文献[9]所提延迟共轭相乘对延迟时间没有要求,其目的是通过多次共轭相乘消除平动的影响。本文在文献[8],文献[9]的基础上规定共轭相乘的延迟为一个周期,分析表明,共轭相乘后信号保留2次及高次平动信息而不包含任何微动分量信息,从而可进一步对平动参数进行估计。结果表明,该方法可在低信噪比条件下对平动参数进行估计,对目标的平动进行高精度补偿。
2 弹道目标中段运动模型
在光学区,目标的散射可等效为多个强散射中心的回波和。对于弹道目标而言,其回波信号可表示为:
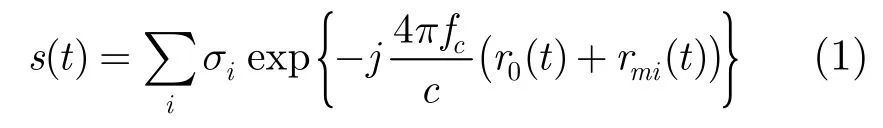
其中fc表示雷达的中心频率,r0(t)表示弹头目标的高速平动导致的位置变化;σi表示第i个散射中心的散射系数,rmi(t)表示微动导致的第i个散射中心相对目标参考中心位置的变化,rmi(t)对应的多普勒频率即为微多普勒频率。r0(t)的存在使得微多普勒频率产生平移、折叠[5]。由于微动周期短,一般为秒级,在短时间(几个微动周期)内,平动速度很大,而平动多普勒变化率较小,可以利用观测时间内某个脉冲测得的速度Vi对回波信号进行统一的预补偿[5]:

rt(t)为预补偿后的平动剩余分量,补偿后信号sr(t)的1阶速度是一个较小量,在观测时间内可认为没有多普勒模糊。
rt(t)可进一步用多项式模型进行描述:
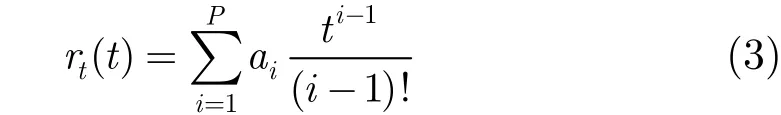
观测时间越短,用于描述rt(t)的阶数越少。在本文中,所对应观测时间为几个微动周期,用3阶多项式模型可较好描述弹道目标的平动[6],即:
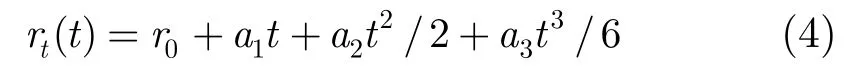
其中r0表示初始距离,a1表示初补偿后剩余的速度,a2表示加速度,a3表示2阶加速度。
为了保证弹头再入大气层的再攻角,弹头通过自旋保持指向,而诱饵释放过程中的扰动将使得自旋目标进动。弹头目标的结构一般是类锥形的,具有旋转对称特性。旋转对称目标的散射特性只和雷达入射方向与目标对称轴的夹角有关,此时,弹头进动所导致的等效散射中心运动可用式(5)模型描述[10]:

其中β(t)表示进动导致的雷达视线方向与旋转对称轴的夹角的变化,(xi, yi)为散射中心在投影平面的坐标。设进动角为θP、进动角速度为ωP,初始相位角为ϕ,平均雷达视线方向在平动坐标系中的俯仰角为γ,从而有[10]:
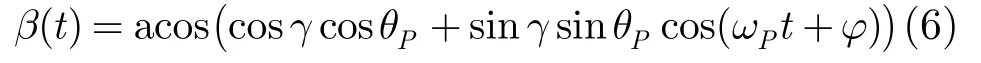
设进动周期为Tp=2π/ωP,可知β(t+Tp)= β(t),从而有rmi(t+Tp)=rmi(t)。即微动导致的位置变化具有周期性,经过时间Tp后各散射中心由于微动导致的位置变化是一致的,而平动不具有此特性。因此,可基于上述差异对平动参数进行估计。
3 基于延迟共轭相乘的平动参数估计
3.1 延迟共轭相乘处理
为了分析简单,首先不妨假设目标只包含一个强等效散射中心,目标的回波信号可表示为:
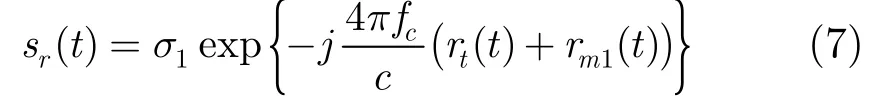
rm1(t)表示微动导致的散射中心微距离变化。延迟共轭相乘处理后有:
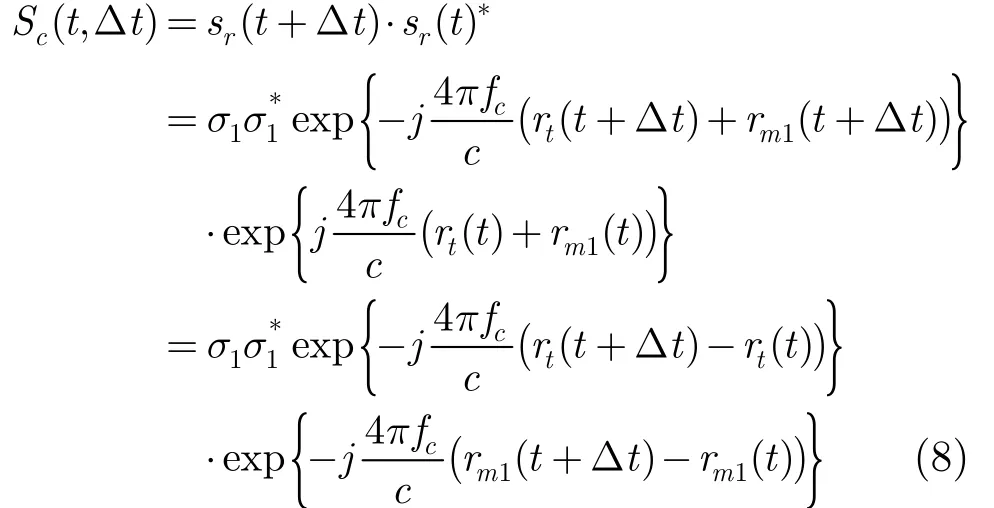
式中rt(t+Δt)-rt(t)仅与雷达的平动参数有关,rm1(t+Δt)-rm1(t)与目标的微动有关。对于弹道目标而言,有:
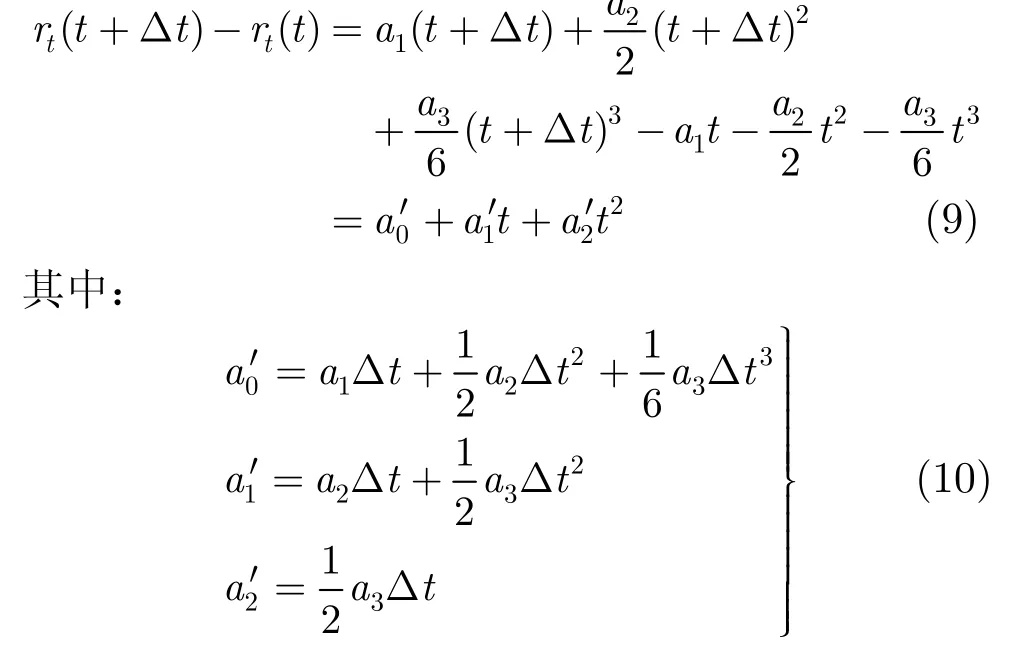
弹道目标进动具有周期性,即rmi(t+Tp)= rmi(t),在平动补偿的基础上,已有许多文献对进动周期估计方法进行了研究[11],所利用特性为回波的周期性变化特性,如幅度变化的周期性。在平动未补偿时,平动信息主要体现在相位项中,对回波幅度没有影响,因此,仍可利用文献[11]所提算法对平动未补偿目标的进动周期进行估计。在此文中假设Tp已知。取δt =TP,则有:
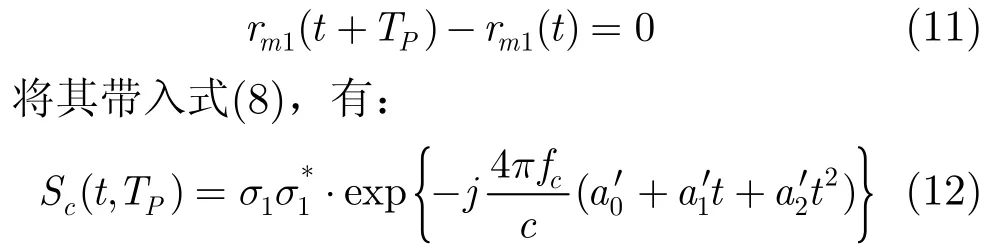
式(12)表明Sc(t, TP)是一个线性调频(Linear Frequency Modulation, LFM)信号,且相位调制参数与目标的平动加速度a2及二阶加速度a3有关。假设利用 LFM 参数估计算法从Sc(t, TP)中提取的LFM 信号分量的频率中心为f0、调频率为γ0,根据式(10)和式(12)可知,f0,γ0可表示为:
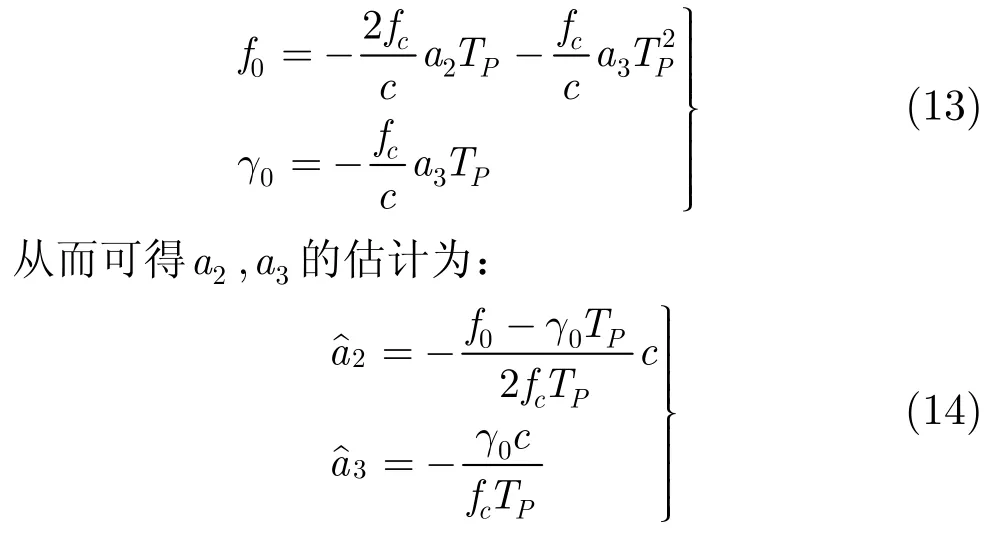
3.2 延迟共轭相乘交叉项分析
当目标包含多个散射中心时,延迟共轭相乘处理将产生交叉项。将式(1)代入式(8),可得:
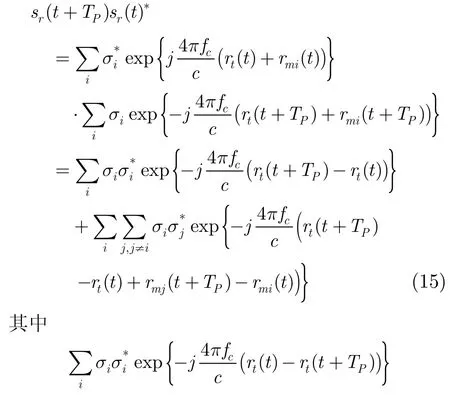
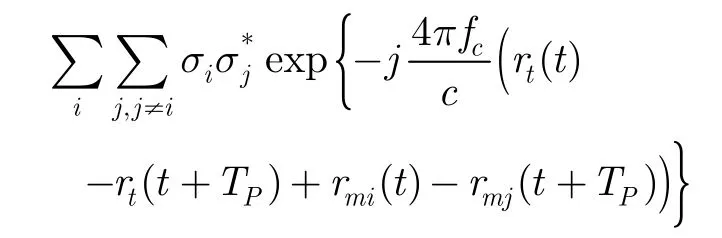
表示各散射中心对应自项的能量和,而表示交叉项。不同散射中心自项所对应的多普勒频率变化一致,表现为参数一致的LFM信号分量,各散射中心自项对应信号在时-频面上是叠加在一起的;而交叉项不可用LFM模型描述,且各交叉项所对应多普勒频率不一致,它们的能量在时-频面上是分散的。因此,利用LFM信号参数估计方法仍可从sr(t+TP)sr(t)∗中正确提取出自项所对应的f0及调频率参数γ0。第4节仿真结果也验证了这一点。
3.3 弹道目标平动参数补偿流程
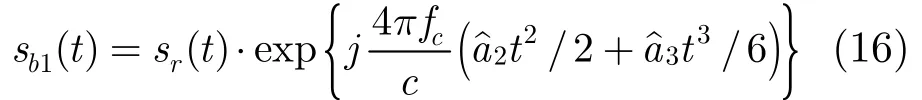
补偿后信号的平动可等效为匀速直线运动,在时频图上表现为频谱的平移。针对匀速直线运动目标的平动补偿,文献[1]提出可根据信号频谱的多普勒中心对速度a1进行估计。估计的基本过程是首先对sb1(t)进行频谱分析,估计出频谱中心,从而有:
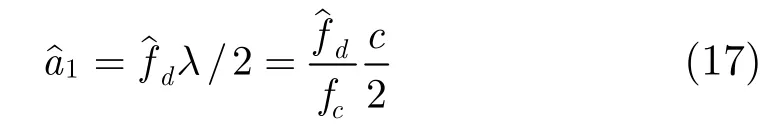
其中λ=c/fc为雷达发射信号的波长。匀速平动补偿的详细信息可参考文献[1]。
在估计出目标速度a1后,可进一步根据a1对sb1(t)补偿,得到平动完全补偿后信号sb(t):

根据上述分析,可得弹道目标中段平动补偿步骤如下所示:
(1) 根据文献[11]所提方法估计进动周期TP,根据式(8)对信号以TP为延迟进行共轭相乘处理,得到Sc(t, TP);
(2) 利用LFM参数估计算法从Sc(t, TP)中提取能量最强的LFM分量,得到,。在本文中,采用文献[12]所提算法提取LFM分量;
(4) 根据式(16)对回波进行高阶平动补偿,得到sb1(t);
(5) 根据文献[1]所提频谱中心法估计目标速度a1;
(6) 根据式(18)得到平动完全补偿后的回波信号,此信号仅包含了目标的微多普勒信息。
4 仿真结果分析
设目标由3个散射中心组成,位置分别如图1(a)所示,设置目标进动,进动周期为2 s,进动角为10°,进动轴与雷达视线方向为55°。平动速度初补偿后剩余的速度为2.5 m/s,加速度为1 m/s2, 2阶加速度为0.5 m/s3,雷达中心频率为3 GHz,脉冲重复频率为200 Hz,观测时间为5 s。利用点散射中心产生目标回波后原始回波信号的时频分析结果如图1(b)所示,由于平动的影响,目标微多普勒频率在时频图上出现了漂移与折叠。以 2 s为间隔,对回波信号进行共轭相乘,所得信号时频分析结果如图2(c)所示,从图中可以看出,最强信号分量在时频图上表现为一条斜线,对应了各散射中心延迟共轭相乘后的自项,可用LFM信号模型描述;同时,交叉项所对应的信号分量幅度较小,验证了 3.2节分析的正确性。利用 LFM 信号参数估计方法得到LFM 信号的中心频率为-60 Hz,调频率为-10 Hz/s,根据式(14)得到目标加速度为1 m/s, 2阶加速度为0.5 m/s2,估计结果与设定值一致。利用估计出的平动参数按照式(16)对高阶平动进行补偿,补偿后信号时频分析结果如图1(d)所示,从图可以看出此时多普勒频率已被“拉平”,仅剩微多普勒信息,根据文献[1]方法,得到目标速度估计结果为2.5025 m/s。
目标参数与雷达参数不变,在不同信噪比下进行蒙特卡罗仿真,得到 a1, a2, a3的估计均方根误差如表1所示。从表1可以看出:当信噪比大于等于-5 dB时,本文算法可对目标的平动加速度及2阶加速度进行高精度估计;而当信噪比大于等于-3 dB时,本文方法可实现对目标速度的有效估计。a1及a2, a3有效估计的起始信噪比门限存在差别,这主要是由于a2, a3是基于延迟共轭相乘处理进行估计的,而a1是在a2, a3估计基础上利用文献[1]所提多普勒中心法进行估计的。
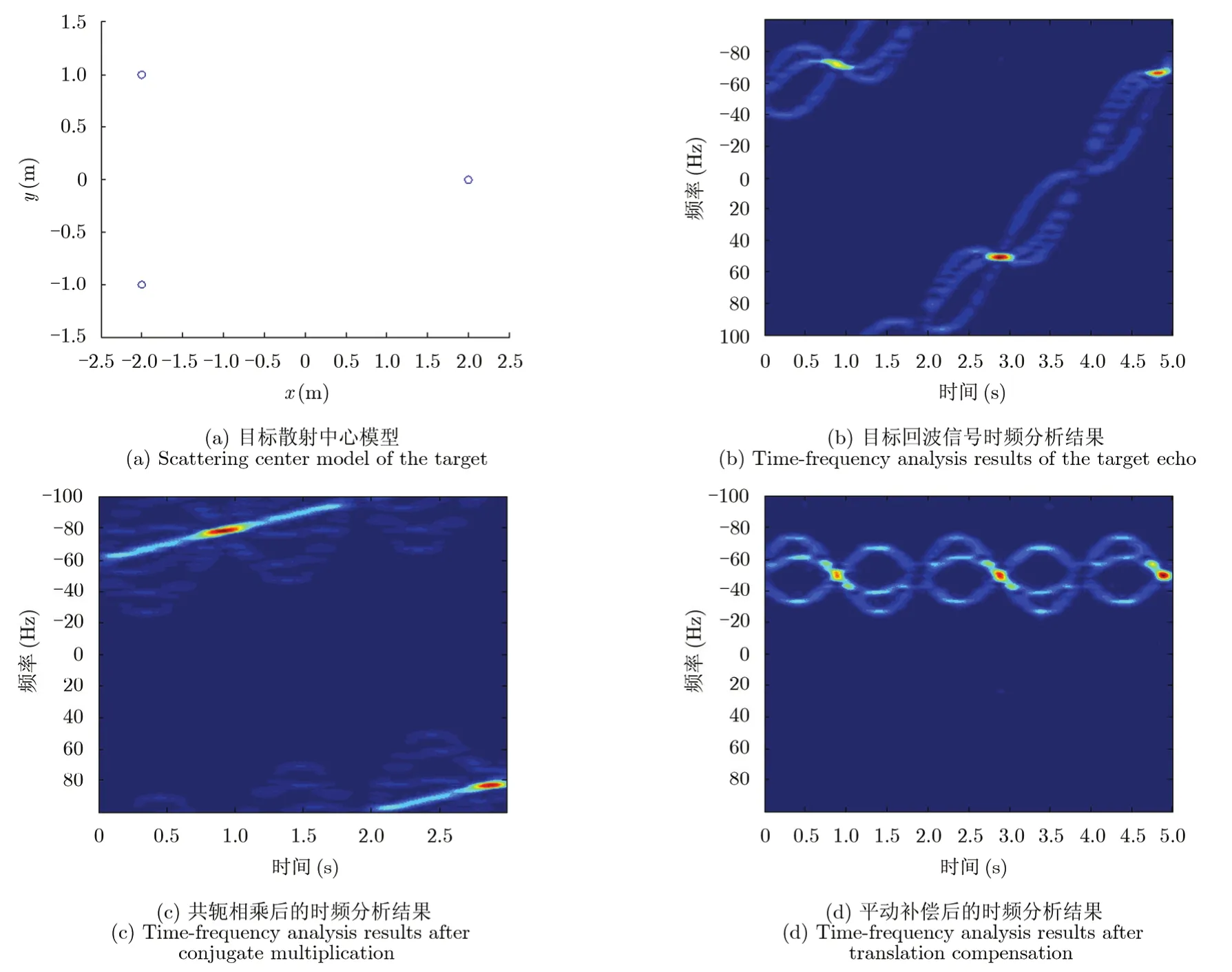
图1 基于共轭相乘的平动补偿过程Fig. 1 Translation compensation based on conjugate multiplication

表1 平动参数估计性能Tab. 1 Estimation performance of translation parameters
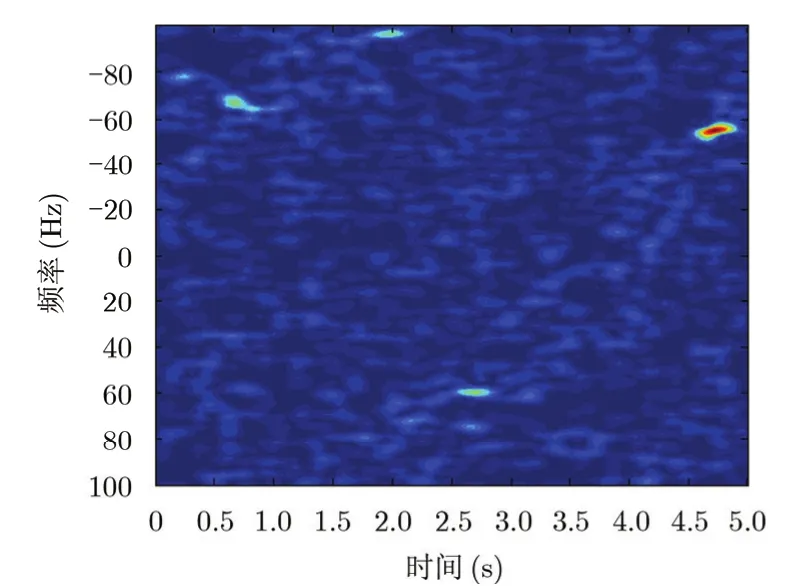
图2 信噪比为-5 dB时的原始信号时频图Fig. 2 Time-frequency analysis results of the target echo (SNR=-5 dB)
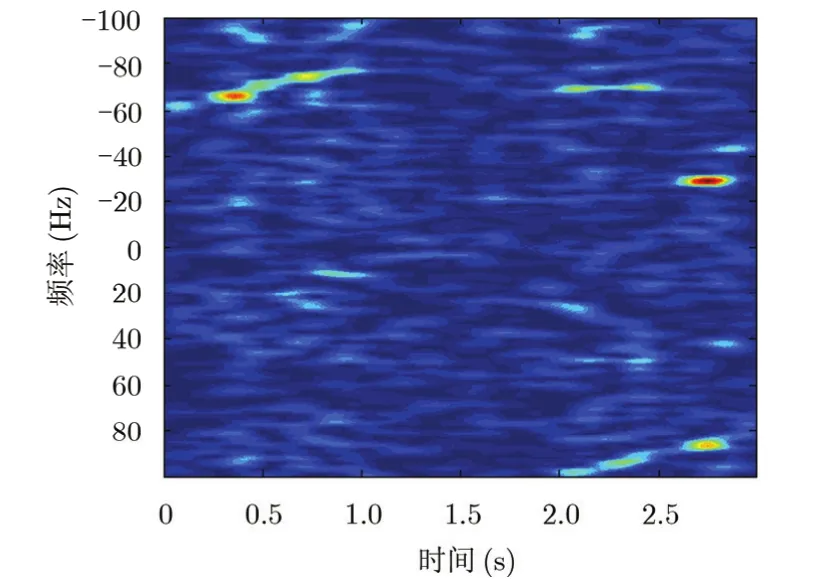
图3 -5 dB时共轭相乘后信号时频图 Fig. 3 Time-frequency analysis results after conjugate multiplication (SNR=-5 dB)
图2给出了-5 dB时某次仿真原始信号的时频分析结果。从图2可以看出,此时频谱图被噪声严重污染,图中不能辨认出散射中心的存在,在此情况下文献[5-7]所提算法将不可用。图3给出了对应信号进行共轭相乘后的信号时频图,从图中可以明显看出线性调频信号分量,因此本文算法仍能对平动加速度及2阶加速度进行准确估计和补偿,这说明本文算法在低信噪比下具有良好的稳健性。这主要是由于当利用本文算法对平动参数进行估计时,各散射中心自项是一致且相干叠加的。
5 小结
针对弹道目标平动参数估计问题,本文在分析中段目标平动及微动特性的基础上,针对微动的周期性特点提出对回波信号进行延迟共轭相乘消除微动的影响,再根据延迟共轭相乘后的信号实现了平动参数估计方法。仿真结果表明,该方法可在低信噪比条件下实现平动参数的高精度估计。
文章分析是针对进动这一微动模式展开的,所利用的特性为进动的周期特性,因此本文算法可推广到任何伴随周期性微动的平动目标之上,实现平动参数的估计。
[1]高红卫, 谢良贵, 文树梁, 等. 速度对微多普勒的影响及其补偿研究[J]. 航天电子对抗, 2008, 24(4): 46-50.
Gao Hong-wei, Xie Liang-gui, Wen Shu-liang, et al.. Research on the influence of velocity on micro-Doppler and its compensation[J]. Aerospace Electronic Warfare, 2008, 24(4): 46-50.
[2]高红卫, 谢良贵, 文树梁, 等. 加速度对微多普勒的影响及其补偿研究[J]. 宇航学报, 2009, 30(2): 705-711.
Gao Hong-wei, Xie Liang-gui, Wen Shu-liang, et al.. Research on the influence of acceleration on micro-Doppler and its compensation[J]. Journal of Astronautics, 2009, 30(2): 705-711.
[3]马启烈, 鲁卫红, 冯存前, 等. 基于微动目标主体信息的平动补偿方法[J]. 现代防御技术, 2013, 42(2): 143-172.
Ma Qi-lie, Lu Wei-hong, Feng Cun-qian, et al.. Translation compensation based on body information of target with micro-motions[J]. Modern Defence Technology, 2013, 42(2): 143-172.
[4]谢苏道, 陈亚伟, 孙俊. 导弹动态回波序列仿真及平动补偿研究[J]. 空军预警学院学报, 2013, 27(3): 169-176.
Xie Su-dao, Chen Ya-wei, and Sun Jun. Simulation of dynamic echoes sequence of missiles and its translational motion compensation[J]. Journal of Air Force Early Warning Academy, 2013, 27(3): 169-176.
[5]杨有春, 童宁宁, 冯存前, 等. 弹道目标中段平动补偿与微多普勒提取[J]. 宇航学报, 2011, 32(10): 2235-2241.
Yang You-chun, Tong Ning-ning, Feng Cun-qian, et al.. Translation compensation and micro-Doppler extraction of ballistic target in midcourse[J]. Journal of Astronautics, 2011, 32(10): 2235-2241.
[6]杨有春, 童宁宁, 冯存前, 等. 利用最强散射点信息的平动补偿与微多普勒提取[J]. 西安电子科技大学学报, 2012, 39(6): 147-153.
Yang You-chun, Tong Ning-ning, Feng Cun-qian, et al.. Translation compensation and micro-Doppler extraction by using the information on the strongest scatter[J]. Journal of Xidian University, 2012, 39(6): 147-153.
[7]罗迎, 柏又青, 张群, 等. 弹道目标平动补偿与微多普勒特征提取方法[J]. 电子与信息学报, 2012, 34(3): 602-608.
Luo Ying, Bai You-qing, Zhang Qun, et al.. Translational motion compensation and micro-Doppler feature extraction of ballistic targets[J]. Journal of Electronics & Information Technology, 2012, 34(3): 602-608.
[8] Yang You-chun, Tong Ning-ning, Feng Cun-qian, et al.. Micro-Doppler extraction of rotating targets based on Doppler rate[C]. 2011 IEEE International Conference on Signal Processing Communications and Computing, Xi’an, 2011: 1-4.
[9] Feng Cun-qian, Yang You-chun, and Tong Ning-ning. Macro-motion compensation and micro-Doppler zooming by multi-level delayed and conjugated multiplication[C]. Spring World Congress on Engineering and Technology, Xi’an, 2012: 1-4.
[10]贺思三, 赵会宁, 冯存前. 多视角距离像序列弹道目标的进动参数估计[J]. 信号处理, 2013, 29(8): 1028-1035.
He Si-san, Zhao Hui-ning, and Feng Cun-qian. Precession parameter estimation for ballistic targets based on multi-aspect range-profile sequence[J]. Journal of Signal Processing, 2013, 29(8): 1028-1035.
[11]肖立, 周剑雄, 何俊, 等. 弹道目标中段进动周期估计的改进自相关法[J]. 航空学报, 2010, 31(4): 812-818.
Xiao Li, Zhou Jian-xiong, He Jun, et al.. Improved autocorrelation method for precession period estimation of ballistic target in midcourse[J]. Acta Aeronautica Et Astronautica Sinica, 2010, 31(4): 812-818.
[12]齐林, 陶然, 周思永, 等. 基于分数阶 Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学(E辑), 2003, 33(8): 749-759.
Qi Lin, Tao Ran, Zhou Si-yong, et al.. Multicomponent LFM signal detection and parameter estimation based on fractional Fourier transform[J]. SCIENCE IN CHINA (Series E), 2003, 33(8): 749-759.

贺思三(1981-),男,湖南湘潭人,博士,空军工程大学讲师,研究方向为弹道目标识别。
E-mail: hessian@163.com
赵会宁(1979-),女,陕西扶风人,硕士,空军工程大学讲师,研究方向为雷达电子对抗技术。
E-mail: zhaohuininghss@163.com
张永顺(1956-),男,空军工程大学教授,博士生导师,研究方向为雷达电子对抗技术。
Translational Motion Compensation for Ballistic Targets Based on Delayed Conjugated Multiplication
He Si-san Zhao Hui-ning Zhang Yong-shun
(The Aerial Defence and Antimissile Institute, Air Force Engineering University, Xi’an 710051, China)
The micro-motion is combined with the high velocity of translation motion for ballistic targets. The translation motion should be compensated for micro-Doppler information extraction. A new method based on delay conjugate multiplication is proposed to compensate the translation motion of ballistic target. By delay conjugate multiplication of the received signal, the micro-Doppler information are canceled out and the translation motion parameters estimation problem is transformed as an multi-polynomial phase signal parameters estimation problem. Thus, the translation parameters can be estimated. Simulation results suggest that the proposed algorithm can achieve high-precision compensation for ballistic targets under low SNR.
Ballistic target; Micro-Doppler; Translation compensation; Delay conjugate multiplication
TN957
A
2095-283X(2014)05-0505-06
10.3724/SP.J.1300.2014.14087
2014-06-04收到,2014-07-20改回;2014-09-16网络优先出版国家自然科学基金(61372166)资助课题
*通信作者: 贺思三 hessian@163.com

