灰色信息系统基于集中有序关系下的知识约简

金玲玲，苏 莉，王喜凤

1.海南师范大学 数学与统计学院，海口 571158

2.安徽工业大学 计算机学院，安徽 马鞍山 243002

灰色信息系统基于集中有序关系下的知识约简

金玲玲1，苏 莉1，王喜凤2

1.海南师范大学 数学与统计学院，海口 571158

2.安徽工业大学 计算机学院，安徽 马鞍山 243002

1引言

粗糙集理论是波兰数学家Pawlak提出的处理不精确、不完备数据的有效工具[1]。经典的粗糙集以完备信息系统作为研究对象，以等价关系为基础，通过等价关系对论域进行分类。但由于噪声和信息缺损等因素影响，许多信息系统并不是基于等价关系的，于是人们将等价关系放宽为相容关系、相似关系等。实际应用中，由于决策者的偏好等原因，大量的信息又是基于优势关系的，文献[2-3]就信息系统中属性值排序问题提出了基于优势关系的粗糙集研究方法，促进了粗糙集的应用和发展。目前处理偏好信息主要定义了两种优势关系，递增偏好有序和递减偏好有序，文献[4-5]讨论了在优势关系下的属性约简。然而这种优势关系不能解决一类属性偏好既不是递增有序也不是递减有序，而是属性值趋向于标准属性值的问题，于是文献[6]建立了一种属性集中有序关系来解决集值系统中的分类问题。

灰色系统理论[7]是20世纪80年代我国学者邓聚龙教授提出，用于解决小样本，贫信息的不确定问题工具，其在分析、建模、预测等方面的独到之处，已被证明具有很高的应用价值。

鉴于基于优势关系下的灰色信息系统约简的研究较少，本文结合粗糙集理论与灰色理论，在集中有序优势关系中引入灰数测度的概念，并以综合优势度为基础，给出度量属性重要度的指标，提出了一种新的优势关系下灰色系统的启发式属性约简方法。

2 灰色信息系统

定义1[8-9]灰数指在某一区间或某个一般的数集内取值的不确定数，用记号“⊗”表示。

灰数有以下几类：

（4）黑数与白数：当⊗∈[-∞，∞]时，即当⊗的上界和下界均为无穷时，称⊗为黑数；当⊗∈且时，称⊗为白数。

（5）离散灰数与连续灰数：在某一区间内取有限个值或可数个值的灰数称为离散灰数；取值连续地充满某一区间的灰数称为连续灰数。

定义2[9]灰数的测度用 μ(⊗)表示，不同类型的灰数其测度定义为：

定义3设灰数⊗1∈，⊗2∈，则⊗1∩⊗2运算有五种情形：

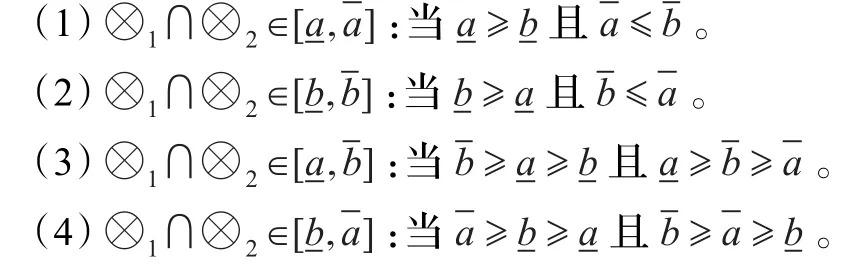
（5）其他取Φ。

定义4[9-10]灰色信息系统GS是一个四元组，即GS= {U，A，V，f⊗}，其中U为对象的非空有限集合，即论域；A为属性集，V=∪Va且Va是属性a的灰描述域，f⊗∶U× A→V为对象的灰描述函数，对于∀a∈A,u∈U，f⊗(u，a)为对象u在属性a对应的灰数，记作ua(⊗)。

3 信息系统中的优势关系和优势度

3.1 优势关系

定义5[11-12]设GS={U，A，V，f⊗}，对a∈A，xi，xj∈U，若任取vj∈f⊗(xj，a)，都存在vi∈f⊗(xi，a)，使vi≥vj，则称xi关于a优于xj，记为 xi≻axj；若任取vj∈f⊗(xj，a)，都存在vi∈f⊗(xi，a)，使vi≤vj，则称 xi关于a劣于 xj，记为 xi≺axj。

对于属性集B⊆A，xi≻Bxj指xi关于B优于xj，反之，xi≺Bxj指xi关于B劣于xj。

定义6给定信息系统GS={U，A，V，f⊗}，B⊆A，优势关系R≥B定义为：

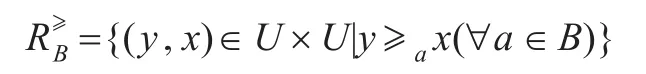
若记[xi]B={xj∈U|(xi，xj)∈}，U={[xi]B|xi∈U}，则称[xi]B为对象 xi的优势类，U为信息系统对象集关于属性B的一个分类。

3.2 集中有序关系

限于篇幅，仅介绍合取集值系统中的集中有序关系。

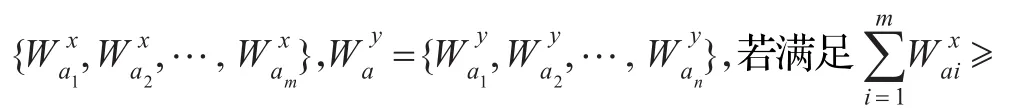
其中，Ma取Va的某个中间值作为标准值。

定义8给定信息系统S={U，A，V，f}，B⊆A优势关系 R∧B≥定义为：

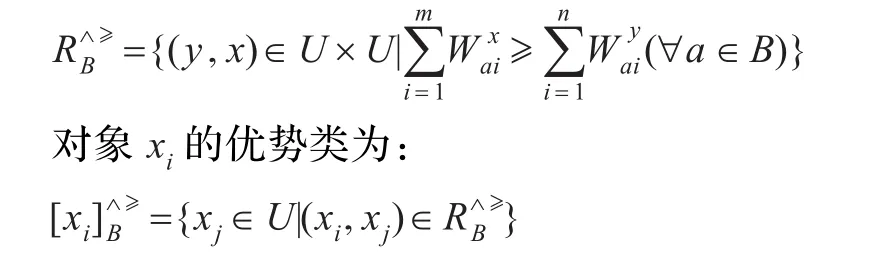
显然 R∧≥B满足自反性、传递性。

3.3 集中有序关系扩展

上述的集中有序关系可应用于离散灰数的信息处理，但不适用于连续灰数的处理，因此结合灰数测度的概念，对集中有序关系进行扩展。

定义9给定灰色信息系统GS={U，A，V，f⊗}，Va、Ma分别表示属性a的值域和标准值，对于 x，y∈U，f⊗(x，a)=Vax，f⊗(y，a)=Vay，若满足Wax=μ(Vax∩Ma)≥μ(Vay∩Ma)=Way，则称在属性a∈A下，y优于x，记为y≻ax。

其中，Ma取Va的某中间段的区间灰数作为标准值。

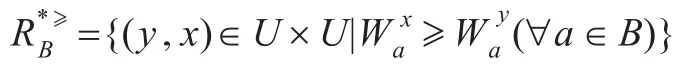
对于x的优势类相应地为：

3.4 优势度和属性重要性度量

定义10[13-14]对于 xi，xj∈U ，对象 xi在属性集 A下优于对象xj的程度为：

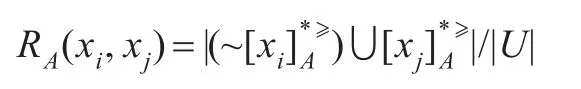
显然有0≤RA(xi，xj)≤1。

对象xi在属性集A下的综合优势度为：

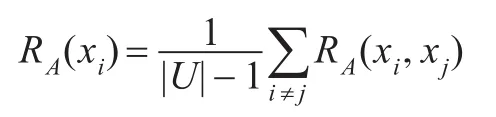
其中0≤RA(xi)≤1，且 xi≻Axj时，RA(xi)＞RA(xj)。RA(xi)的大小反映了xi在属性集A下的优势程度。按照RA(xi)的大小排序后其序组成向量，记为rA=(r1，r2，…，rn)。

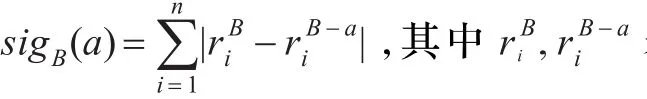
可见 sigB(a)≥0，若sigB(a)=0时，表明属性a对 B是不必要的，否则其值越大，属性a对B的重要性越大。

4 基于优势度的启发式属性约简

知识约简是粗糙集理论中的一个重要概念，根据扩展后的集中有序关系，以优势度作为属性重要性的启发信息，寻找一个能保持优势关系 R*≥下的最小属性子集。因此下面讨论灰色系统在优势关系R*≥下的属性约简方法。

定义12设GS={U，A，V，f⊗}是一个优势信息系统，∀B⊆A，a∈B，属性a对B的重要性为sigB(a)，当sigB(a)＞0，说明a是B中必要的；当sigB(a)=0，说明a是B中不必要的。若∀a∈B都为B中必要的，则称B为独立的，否则，称B是依赖的。

性质1属性a∈B在属性集B中是必要的当且仅当sigB(a)＞0。

性质2Core(B)={a∈B|sigB(a)＞0}。

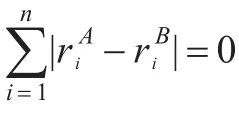
算法描述：

根据性质2求出信息系统中属性A的核，其次选择对核属性重要性最大属性依次加入核中，直到序向量各分量差值之和为0为止，得到一个最小约简。

输入 一个优势信息系统GS={U，A，V，f⊗}

输出 该系统的核Core(A)和约简Red(A)

步骤1给定一组标准值M，计算∀xj∈U，∀aj∈A下的。

步骤6输出Core(A)和Red(A)，算法终止。

5 实例分析

表1[15]所示的是一个完备灰色信息系统，对象集U= {x1，x2，…，x6}，属性集 A={a1，a2，a3，a4}，属性集 A中的偏好属性集中有序。其中，Va1=[0.3，0.9]，可取其中间分段作为 Ma1的标准值，即 Ma1=[0.5，0.7]，同理可令Ma2=[0.25，0.35]，Ma3=[0.4，0.5]，Ma4=[0.6，0.7]。

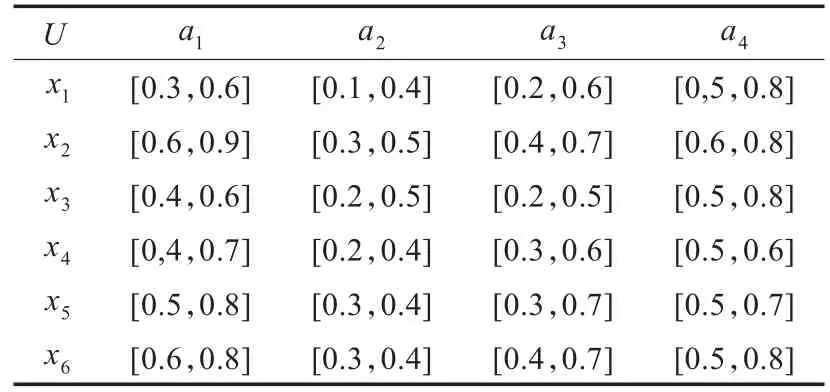
表1 一个完备灰色信息系统

步骤1根据定义9，计算各对象在优势关系R*≥下的Wxj

aj的值，如表2所示。

表2 计算结果

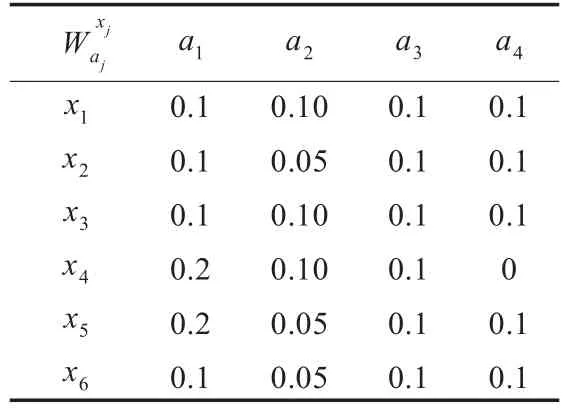
表2 计算结果

Wxj aj x1 x2 x3 x4 x5 x6 a1 0.1 0.1 0.1 0.2 0.2 0.1 a2 0.10 0.05 0.10 0.10 0.05 0.05 a3 0.1 0.1 0.1 0.1 0.1 0.1 a4 0.1 0.1 0.1 0 0.1 0.1

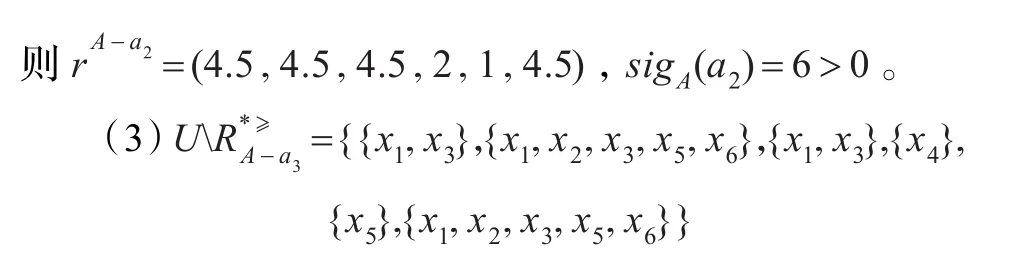
删除属性a3后，基于优势关系的集合均未发生变化，因此sigA(a3)=0。

步骤4将所有重要度大于0的属性并入Core(A)，可得R=Core(A)={a1，a2，a4}。

例中信息系统的约简结果与文献[15]完全一致，通过计算属性的重要度来确定核属性，较文献[15]通过分辨矩阵求核属性，节省了大量的储存空间。此外，约简过程中采用迭代方法，利用减小选择属性集的大小提高了属性约简的效率。

6 结束语

由于现实应用中，信息存在不完全性和复杂性。本文结合粗糙集和灰色系统理论两种不确定信息处理工具的优势，探讨了集中有序优势关系下灰色信息的分类，提出了一种基于优势度的启发式属性约简算法，该算法能从搜索空间排除不重要的属性，避免属性重要性的重复计算，提高了搜索效率，为灰色信息系统的知识发现和规则提取提供了一种新的方法。

[1]Pawlak Z.Rough sets：theoretical aspects reasoning about data[M].Dordrecht，UK：Academic Publishers，1991.

[2]Greco S，Matarazzo B，Slowingski R.Rough sets theory for multicriteria decision analysis[J].European Journal of Operational Research，2001，129（1）：1-47.

[3]Greco S，Matarazzo B，Slowingskir.Rough approximation by dominance relation[J].International Journal of Intelligent Systems，2002，17（2）：153-171.

[4]徐伟华，张文修.基于优势关系下不协调目标信息系统的知识约简[J].计算机科学，2006，33（2）：182-184.

[5]Shao M W，Zhang W X.Dominance relation and rules in an incomplete ordered information system[J].International Journal of Intelligent Systems，2005，20（1）：13-27.

[6]张腾飞，魏立力.集中有序集值信息系统[J].计算机工程与应用，2014，50（16）∶140-145.

[7]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002.

[8]Deng J L.Control problems of grey system[J].System& Control Letter，1982，1（5）：288-294.

[9]吴顺祥.灰色粗糙集模型及其应用[M].北京：科学出版社，2009.

[10]吴顺祥，林理华，周志文.基于灰色信息系统的优势关系及其属性约简方法[J].厦门大学学报：自然科学版，2009，48（4）：482-488.

[11]陈子春，刘鹏惠，秦克云.集值信息系统基于优势关系下的知识约简[J].计算机科学，2009，36（12）：176-193.

[12]林耀进，李进金，林梦雷.优势关系下的集值序值信息系统[J].计算机应用，2011，31（12）：3240-3246.

[13]张文修，仇国芳.基于粗糙集的不确定决策[M].北京：清华大学出版社，2005.

[14]廖启明，龙鹏飞.基于属性重要性的粗糙集属性约简方法[J].计算机工程与应用，2013，49（15）：130-132.

[15]林耀进，李进金，吴顺祥，等.不完备灰色信息系统的粗集模型[J].计算机应用，2010，30（2）：3374-3376.

JIN Lingling1,SU Li1,WANG Xifeng2

1.School of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China
2.School of Computer Science,Anhui University of Technology,Ma’anshan,Anhui 243002,China

Attribute reduction is very important to knowledge acquisition in rough set theory.Considering the reality that many attributes values are uncertain in real information system,ordered concentration relation combined with gray system theory is expanded.A kind of preference relation that attribute values tend to the standard values is established in gray information system.The significance of attribute is defined and the degree of dominance is used as heuristic information. On this basis,the algorithm of attributes reduction is proposed to make it suitable for the information system which attributes valued continuous gray number.A practical operation method for computing reduction is given and the feasibility of algorithm is verified via case.

gray system;ordered concentration;dominance relation;knowledge reduction;standard value

属性约简是粗糙集理论进行知识获取的核心问题之一。针对现实信息系统中属性值取值不确定的情况，结合灰色系统理论对集中有序关系进行扩展，建立了灰色信息系统中趋于某个标准值的一种偏好关系，并以集中有序关系下的优势度为启发式信息，给出了属性的重要性度量，在此基础上提出了适合于属性值为连续灰数的信息系统的属性约简算法，给出了约简的实际操作方法，并通过实例验证了算法的可行性。

灰色系统；集中有序；优势关系；知识约简；标准值

A

TP18

10.3778/j.issn.1002-8331.1302-0013

JIN Lingling,SU Li,WANG Xifeng.Knowledge reduction of gray information systems based on ordered concentration relation.Computer Engineering and Applications,2014,50（24）：139-142.

海南省自然科学基金（No.610221，No.114005）。

金玲玲（1976—），女，讲师，研究领域为粗糙集理论与应用；苏莉（1982—），通讯作者，女，博士，讲师，研究领域为粗糙集；王喜凤（1980—），女，博士，研究领域为粗糙集，Web服务可靠性。E-mail：hnjll2003@126.com

2013-02-04

2013-04-03

1002-8331（2014）24-0139-04

CNKI网络优先出版：2013-04-18，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130418.1618.013.html