基于划分的高效异常轨迹检测

陈 刚，钱 猛，刘 金

中国工程物理研究院 计算机应用研究所，四川 绵阳 621900

基于划分的高效异常轨迹检测

陈 刚，钱 猛，刘 金

中国工程物理研究院 计算机应用研究所，四川 绵阳 621900

1 引言

随着多种移动定位、传感器网络和无线通信技术的发展，人们可以收集和存储越来越多的轨迹数据[1]，如何从这些数据中发现异常模式引起了许多研究人员的注意[2-4]。然而，现存的方法由于采用的轨迹描述方法和匹配（距离）函数的不同，导致挖掘算法在检测结果和检测效率方面存在诸多不同。

Knorr等人利用传统的基于距离的异常挖掘方法检测数据集中的异常轨迹[5-7]。由于该方法利用的都是轨迹的全局属性，它忽略了轨迹间的局部差异，因此，该算法只能应用于长度较短且较为简单的轨迹。

Li等人提出了基于轨迹代表模式motifs的异常轨迹检测算法[8]，它使用聚类方法从滑动窗口中收集motif，然后用分类的思想过滤异常轨迹。该算法由于采用了分类的思想，因此在实际应用中需要寻找较为标准的训练集。

J.-G Lee等人提出基于二阶段划分思想的异常轨迹处理算法TRAOD[9]，它首先将每条轨迹划分为多个连续线段的组合，然后采用Hausdorff距离[10-12]来计算任意两个线段之间的距离，从而挖掘出异常轨迹片段。TRAOD算法较好地解决了长轨迹间的匹配问题，但它同时存在以下几个问题：首先，使用近似方法获得的线段同样会隐藏轨迹的部分局部特征；其次，Hausdorff距离这种度量方法并不符合欧式空间的标准，进而无法使用传统的索引方法来提高计算效率；再次，Hausdorff距离仅依赖于轨迹的形状，轨迹的其他运动特征，例如运动方向和速度等，并没有考虑进匹配函数中。例如图1所示的三条轨迹，假设其他轨迹的运动规律与T1类似，可以很容易发现，T2和T3都是异常轨迹，因为T2虽然运动速度与T1一致，但是运动方向不同，T3虽然运动方向一致，但是速度却比其他轨迹要快，TRAOD算法在检测这类异常轨迹时便有一定的难度。

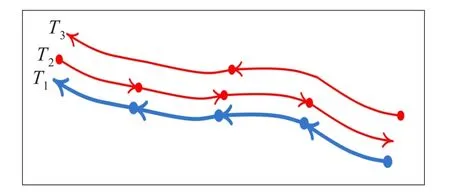
图1 轨迹的运动规律

针对上述问题，本文提出了基于划分的异常轨迹检测方法，它首先定义了一种新的异常轨迹判定方法，其次设计了一种索引结构网格索引树来提高挖掘效率，该结构在时间和空间方面均优于传统的空间划分方法，尤其是在维度的适用性方面有较大的提高。

2 异常轨迹的基本概念和描述

随着探知技术和用户需求的日益提高，轨迹数据集的属性也在不断地发生变化。首先，轨迹在时间和空间上的深度和广度都得到扩展，所获取到的运动规律随时间和空间的变化一直在变化。其次，用户对挖掘算法的精度和效率也提出了越来越高的要求。针对这种现象，本文引入了轨迹局部异常点的概念，根据Apriori性质[13-15]，如果某个轨迹片段不是异常的，那么组成该片段的轨迹点必然不是异常的，同样，如果某个轨迹不是异常的，那么组成该轨迹的轨迹片段同样不是异常的，从而将转化为传统的异常轨迹点检测问题。为了将每个轨迹点异常度的计算限制在其周围的局部邻域内，下面给出一些相关的概念和描述。

定义1（局部轨迹点）假设轨迹在两个连续采样点之间是均匀连续的，可以将轨迹视为无穷个轨迹点的集合，记为T=p1p2…pn，其中 pi(1＜j＜n)称为局部轨迹点，记作 pj∈T。

定义2（轨迹瞬时矢量）假定轨迹的属性集为A= {A1，A2，…，Ad}，d为属性维度，在一个采样时刻t，轨迹Ti对应的轨迹点为 pj，该时刻轨迹的属性值为 Aj= {a1，a2，…，ad}，其中ak(1≤k≤d)为Ak的瞬时值，可以将Aj视作轨迹点 pj的瞬时矢量，记作 pvj={a1，a2，…，ad}。

定义3（轨迹局部距离）轨迹点m∈Ti，n∈Tj，m和n的瞬时矢量分别是 Am，k和 An，k，其中1≤k≤d，则m与n之间的距离为：

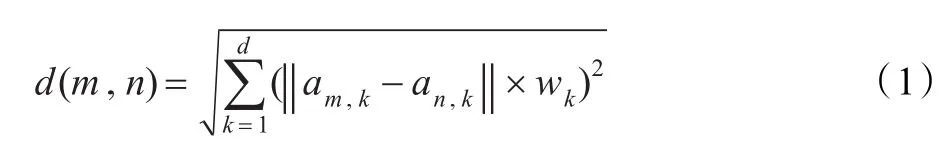
其中wk≥0是用户给定的维度权值参数。

定义4（核心轨迹点）设trω-set(p)表示 p轨迹点ω-邻域内包含的轨迹对象，trω-set(p)={T|o∈T∧o∈pω-set}，给定参数Minpts，若|trω-set(p)|＞Minpts，则称 p为核心轨迹点。

定义5（局部异常轨迹点）给定轨迹数据集，对应的轨迹点集合为P，o∈P，o不被包含在P的任何一个核心轨迹点的ω-邻域内，且|trω-set(o)|≤Minpts，则称o为局部异常轨迹点。

定理1轨迹点m为异常轨迹点的充要条件是m是非核心轨迹点，并且m的ω-邻域（以m为圆心，半径为ω的区域）与核心轨迹点集不存在交集。

证明（充分性）由于m是异常轨迹点，根据定义可知，|trω-set(m)|≤Minpts且m位于所有核心轨迹点的ω-邻域之外。因此m即为非核心轨迹点，其ω-邻域与核心轨迹点集也不存在交集。

（必要性）如果m为非核心轨迹点，那么|trω-set(m)|≤Minpts，又因m的ω-邻域与核心轨迹点集没有交集，即m不被包含在任何核心轨迹点的ω-邻域内。根据定义可知，m为异常轨迹点。

定义6（异常轨迹片段）给定阈值δ，轨迹片段Lk= pipi+1…pj（i＜j≤N，N为轨迹点个数）为异常轨迹片段，当且仅当满足：

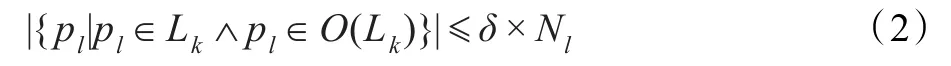
其中O(Lk)是轨迹片段的异常轨迹点集，Nl是轨迹片段的轨迹点集。

定义7（轨迹异常度）一条轨迹T的异常度TOF（Trajectory Outlier Factor）为异常轨迹片段在整条轨迹长度中的比例，即O(T)为轨迹T的异常片段集合。

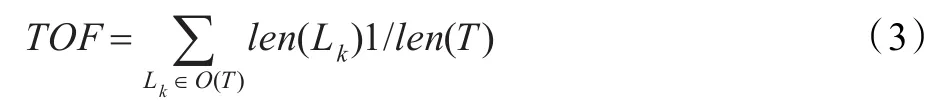
图2中有四条轨迹，P1，P2，P3是轨迹T3上的三个轨迹点，可以发现，无论是空间位置，还是速度方向，这三个点都是异常轨迹点。它们组成异常轨迹片段L1和L2，如果L1和L2的长度和占T3的比例超过一定阈值，则T3就是异常轨迹。

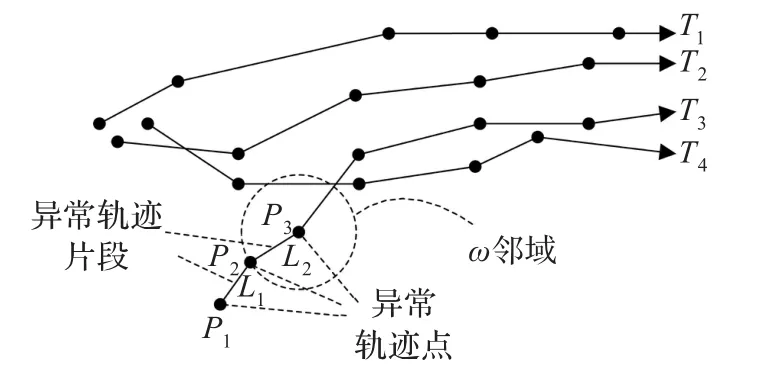
图2 异常轨迹点示例

在现实的轨迹采集中，由于采样频率和移动物体运动速度的不同，导致轨迹在轨迹点的疏密程度上有差异，因此会造成一定的计算误差，所以在实际操作中要对轨迹进行基于距离的线性插值。

3 异常轨迹检测的朴素算法

假设给定轨迹数据集TS={Ti|1≤i≤n}，朴素算法的基本思想就是通过将每条轨迹上的轨迹点逐一与其他轨迹点进行比较来找出异常轨迹点，然后再根据定义来判断异常轨迹。图3给出了朴素算法的伪代码。

图3 异常轨迹检测的朴素算法

下面以距离计算为基本单元分析一下朴素算法的计算复杂度。给定一条轨迹Ti，包含ti个轨迹点，那么对于两条轨迹Ti和Tj，需要计算距离的次数为ti×tj，假定两个轨迹点之间的距离计算复杂度为u，则轨迹Ti和Tj之间的匹配复杂度为：

由于轨迹数量众多，因此朴素算法的计算复杂度为：

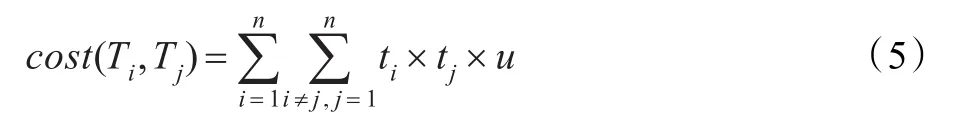
设每条轨迹具有相同数量的轨迹点，即ti=tj=t，那么朴素算法的计算复杂度为：

4 基于划分的异常轨迹检测

在搜索轨迹点的邻近点个数时，为了避免全局空间的搜索，本文使用空间划分的方法将数据的搜索区域划分为若干不重叠的超矩形单元，将异常点的检测限制在局部空间内。与传统的空间划分不同的是，为了提高检索效率和保持网格的位置关系，本文设计了一种网格索引结构，只存储非空网格，同时保持网格间的邻近关系，使得最近邻搜索更加高效地完成。

4.1 网格索引树（Grid Index Tree）

假设G={G1，G2，…，Gk}是一个k维的有序域集合，数据集 X={x1，x2，…，xN}表示 N个点的集合，X的取值范围被G完全覆盖，称G为X的覆盖集。现将数据集 X的覆盖集G的每一个维度划分为m个相等的单元，从而将空间划分为超矩形单元集合P。每个单元C的空间位置表示为{c1，c2，…，cd}，其中，ci为大于或等于0的整数，d为数据维度数目。

k维覆盖集划分后的单元数为md，当覆盖集的每个维度跨度很大时将导致m较大，且维度个数d也较大时，也会导致单元数量的庞大。在实际中，划分后会有大量的空单元产生，为此，设计了网格索引树，只索引非空单元。

定义8（网格索引树GI-Tree）

覆盖集G划分后生成的GI-Tree结构定义如下：

（1）GI-Tree共有d+1层，其中d是G的基数。

（2）除d+1层外，GI-Tree的每一层对应G的一个维度，从第1层到第d层的维度排序遵循事先约定的顺序。

（3）第i层(i≠d+1)中的每个节点存储的内部节点是升幂排序的，记录格式为（cNO，NextPointer），其中cNO是该单元在第i维上的序列号，NextPointer为下一层指针；如果i=d+1，则节点记录格式为（cNO，NextPointer，lk），NextPointer指向叶节点，lk为单链表，保存落入该单元的数据对象。

（4）从根节点到叶节点的一条路径唯一约束一个单元。

图4（a）是一个三维的划分立方体，每个维度等分为4个单元，蓝色单元表示有存储数据。图4（b）为对应的GI-Tree，前三层分别对应数据三个维度（约定的维度顺序为X→Y→Z），最后一层为数据存储层。X维分为4段，但只有1，2，4非空，所以GI-Tree的第一层节点有3个内部节点，以此类推。

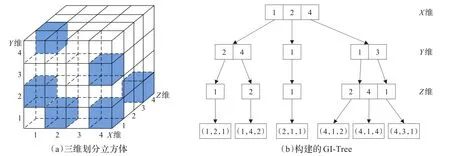
图4 GI-Tree实例

GI-Tree的优势如下：

（1）GI-Tree可以有效地保持数据的邻近关系，在原始划分中相邻的两个单元，在GI-Tree中也是邻近的，这有利于实现数据的高效邻域检索，提高整个算法的效率。

（2）GI-Tree只索引非空单元，这对于轨迹数据尤为重要。轨迹数据的一些维度，例如空间位置，其空间跨度很大，而且移动对象一般呈现出群体行为，这导致在轨迹数据的划分中空单元的数量远远大于非空单元的数量。

4.2 GI-Tree索引的维护算法

下面介绍GI-Tree的构建和范围查询算法。

4.2.1 GI-Tree的构建算法

构建GI-Tree的过程是依次将数据集中的各个点插入到树中。子程序InsertPoint以约定的维度顺序将数据对象在各个维度上的单元在树中查找相应的路径，如果该路径已经存在，将对象插入叶节点的单链表中，否则，从当前一层创建以下各层的节点。GI-Tree创建算法如图5所示。

图5 GI-Tree创建算法

4.2.2 GI-Tree的范围查询

在空间网格中，点p的k近邻是这样一个集合，它包含了以p为中心，以k为厚度的超矩形体内的所有单元。如图6所示，点p的1-邻域是指包围目标立方体且厚度为1单元块，包括8个灰色单元。

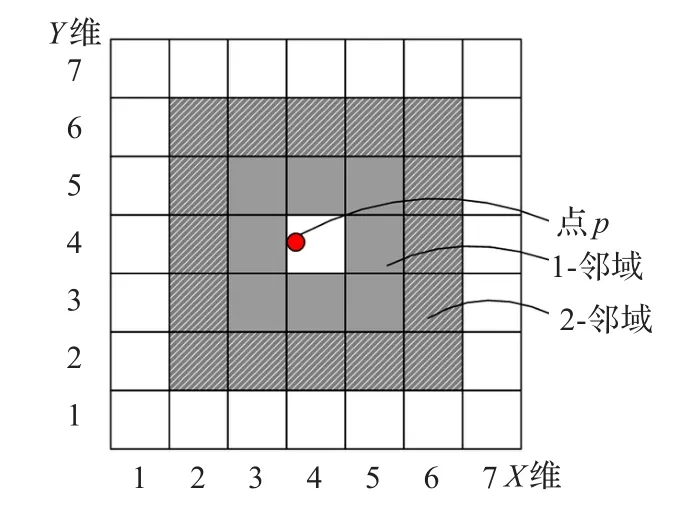
图6 k近邻查询

基于GI-Tree的范围查询算法如图7所示。

图7 范围查询算法

4.3 异常轨迹检测算法

4.3.1 基于GI-Tree的异常轨迹点检测算法

算法4是本文提出的基于GI-Tree的异常轨迹点检测算法。首先计算经过每个单元的轨迹数目，如果大于阈值Minpts则将其标记为red，表明该单元中的轨迹点都不是异常的，否则标记为white。然后针对white单元中的每个轨迹点，根据定义5和算法4判断是否异常。异常轨迹点检测算法如图8所示。

图8 异常轨迹点检测算法

4.3.2 异常轨迹检测算法

算法5给出了异常轨迹检测的完整算法，该算法首先对轨迹数据库做基于距离的线性插值（步骤1），然后构建GI-Tree（步骤2），在检测出异常轨迹点后，根据定义计算轨迹的异常度（步骤3），最后输出异常轨迹（步骤4）。异常轨迹检测算法如图9所示。

图9 异常轨迹检测算法

4.3.3 性能分析

在空间复杂度方面，设每个空间划分单元的存储代价为c，每个维度均匀划分为m个单元，则GI-Tree索引的单元数为(1-s)×md，其中s表示轨迹点集在空间的分布情况，分布均匀时，s趋近于0，分布越不均匀，s就越趋近于1。在真实的轨迹数据集中，轨迹点的分布往往是不均匀的，所以(1-s)×md＜＜md，即该算法的空间复杂度SC＜＜md×c。

在时间复杂度方面，步骤1的时间复杂度为O(nu)，nu为线性插入的轨迹点个数。步骤2是建立网格索引树，假定轨迹点均匀分布，d个维度共划分为md个单元，则建立的GI-Tree共有d+1层，每个非叶节点的内部节点为m个。由于内部节点是排序的，因此每插入一个轨迹点，每层都需要进行lbm次比较，即一次完整的插入过程需要比较d×lbm次。所以，n条轨迹的建树过程需要n×d×lbm次比较。在步骤3中仅考虑GI-Tree的搜索和计算代价，GI-Tree的每层内部查找为二分查找，因此一次查找花费O(dlbm)，计算代价与ω和d成正比，即O(ωd)。设有n条轨迹，平均每条轨迹中有t个轨迹点，则步骤3的计算复杂度为O(dωdlbm×n×t)。

5 实验结果

这一章对本文提出的异常检测算法在有效性和性能方面进行测试。本章的全部实验所使用的数据来自于1849年至2006年大西洋飓风中心运动轨迹（http：// weather.unisys.com/hurricane/index.html），维度信息包括经纬度、最大风力、压力等。本文采用的数据为：（1）数据1，1849年到2006年的轨迹，包含20 371个轨迹点，1 278条轨迹；（2）数据2，1950年到2006年的轨迹，包含19 581个轨迹点，608条轨迹；（3）数据3，1990年到2006年的轨迹，包含7 301个轨迹点，224条轨迹，维度信息采用了经纬度、风力和速度矢量共5维。

实验环境：Windows XP操作系统，Intel Pentinum Dual 2.8 GHz CPU，2 GB内存。开发环境：Microsoft Visual Studio 2005。

5.1 算法的效果分析

为了验证算法的效果，本文以TRAOD算法作为比较算法，实验数据采用数据2和3。从图10（a）和（b）中可以发现，TRAOD算法能够发现轨迹稀疏区域的异常轨迹和拥有异常移动路径的轨迹，也就是说，TRAOD的结果只依赖于轨迹的形状。

图10 与TRAOD算法的检测效果对比

图10（c）和（d）显示了本文提出的算法在同样两个数据集中检测出的异常轨迹的情况(ω=26，δ=0.7，Minpts=10)，从结果中可以很容易发现，除了TRAOD能够检测出的那些具有异常形状的轨迹外，本文的算法还能够检测那些拥有更快的移动速度的异常轨迹（图中圆圈标示），而在TRAOD算法中，这些异常轨迹的路径由于与其他轨迹路径相似而被认为是正常轨迹。因此，本文提出的异常轨迹判定算法要比TRAOD更加具有现实意义。

5.2 参数影响

本文算法主要涉及到如下参数：ω，Minpts。下面以数据3作为实验数据来测试算法，分析不同参数对实验结果的影响。

邻域半径ω对算法的影响最大，不但直接决定了算法的计算代价，而且较为明显地影响算法检测出的异常轨迹的数目。从图11可以发现，随着ω的增大，异常轨迹的数目在逐渐减少，这是因为：ω值越大，算法需要在更大范围内查询与对象轨迹运动规律不相匹配的轨迹，有些轨迹尽管在其较近邻域具有特殊的运动规律，但查询范围增大却和较远区域的轨迹具有相似的运动规律。同时可以看出，ω值越大，算法的执行时间就越长。因此，为ω设定一个合理值不仅有助于提高计算效率，而且对算法的检测效果也有较大提高。

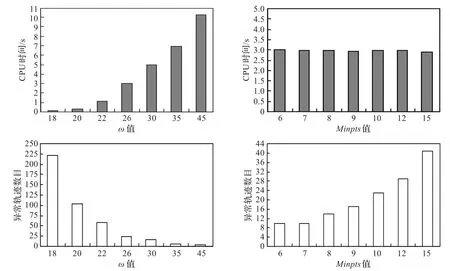
图11 不同参数下算法的执行时间和检测效果对比

参数Minpts表示轨迹的局部匹配的精度，从图11可以看出，当Minpts增大时，算法检测出来的异常轨迹数目在减少，这是因为Minpts增大表明算法对异常的容忍度在增加，Minpts越大，异常轨迹的数目就越少。

从表1中可以发现，本文所提出的算法在计算效率方面远远超过TRAOD算法，虽然TRAOD算法采用了粗细结合的分段方法来减少邻域轨迹段的个数，但由于不能够索引轨迹段，算法的计算复杂度非常大。同时，TRAOD算法采用的度量方法也增加了计算代价。

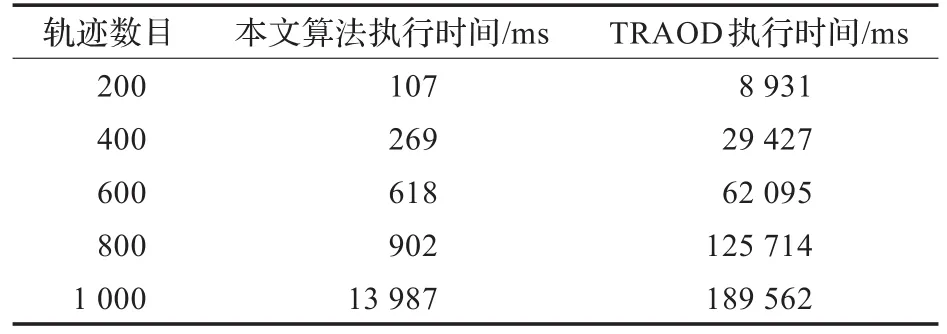
表1 算法执行效率的对比

图12 内存使用情况

为了测试算法的空间复杂度，本文分别使用500条轨迹和200条轨迹，分别测试使用传统网格划分和使用网格索引树算法的最大内存占用情况。从图12中可以发现，随着网格单元数目的增加，内存的占用呈线性增长的趋势，但是采用网格索引树时，内存使用增长率远远小于传统的网格划分方法，主要原因是网格索引树只索引非空网格单元，从而大大降低了内存占用量。

6 结束语

随着无线传感技术和定位服务的发展，挖掘轨迹数据库中蕴含的异常信息已经成为当前的研究热点。本文针对轨迹数据的运动规律和特征，结合空间划分的方法，提出了一种基于网格索引的异常轨迹检测方法。实验结果表明本文提出的算法不仅提高了异常轨迹的挖掘效率，而且能够挖掘出更富现实意义的异常轨迹。

本文提出的算法同样遇到了参数敏感的问题，需要领域专家的参与或多次尝试才能确定合适的参数值。同时，本文的算法目前只能适用于静态历史轨迹数据库，因此，本文的后续工作包括研究自适应参数和研究从轨迹流中即时发现异常轨迹的算法。

[1]Guting G H，Schneider M.Moving objects databases[M]. [S.l.]：Morgan Kaufmann，2005：217-224.

[2]Bu Y，Chen L.Efficient anomaly monitoring over moving object trajectory streams[C]//SIGKDD，Rhode Island，USA，2009：159-168.

[3]Li X，Li Z，Han J，et al.Temporal outlier detection in vehicle traffic data[C]//Proceedings of ICDE，2009：1319-1322.

[4]Ge Y，Xiong H，Zhou Z H，et al.Top-eye：top-k evolving trajectory outlier detection[C]//Proceedings of CIKM，2010：1733-1736.

[5]Knorr E M，Ng R T.Algorithms for mining distance-based outliers in large datasets[C]//Proceedings of 24th VLDB，New York City，1998：392-403.

[6]Knorr E M，Ng R T.Finding intensions knowledge of distance-based outliers[C]//Proceedings of 25th VLDB，Edinburgh，Scotland，1999：211-222.

[7]Knorr E M，Ng R T，Tucakov V.Distance-based outlier：algorithms and applications[J].VLDB Journal，2000，8（3）：237-253.

[8]Li X，Han J，Kim S，et al.ROAM：rule and motif-based anomaly detection in massive moving object data sets[C]// Proceedings of 7th SIAM International Conference on Data Mining，Minneapolis，Minnesota，2007：296-307.

[9]Lee J G，Han J，Li X.Trajectory outlier detection：a partition-and-detect framework[C]//Proceedings of ICDE，2008.

[10]Lee J G，Han J，Whang K Y.Trajectory clustering：a partition-and-group framework[C]//Proceedings of ACM SIGMOD，Beijing，China，2007：593-604.

[11]Chen J，Leung M K H，Gao Y.Noisy logo recognition using line segment Hausdorff distance[J].Pattern Recognition，2003，36（4）：943-955.

[12]Lee J G，Han J，Li X，et al.TraClass：trajectory classification using hierarchical region-based and trajectory-based clustering[C]//Proceedings of PVLDB，2008.

[13]Agrawal R，Srikant R.Fast algorithm for mining association rules[C]//Proceedings of the 20th International Conference on VLDB，Santiago，Chile，1994：487-499.

[14]Agrawal R，Srikant A R.Mining sequential patterns[C]// Proceedings of ICDE，1995：3-14.

[15]Han J，Pei J，Yin Y.Mining frequent patterns without candidate generation[R].School of Computing Science，Simon Fraser University，1999.

CHEN Gang,QIAN Meng,LIU Jin

Institute of Computer Application,China Academy of Engineering Physics,Mianyang,Sichuan 621900,China

As the development of mobile computing technology and GPS-enabled mobile devices,the services of moving object receive more and more attention.And trajectory outlier detection is a widely appealing application.In this paper,a novel detection algorithm is proposed to mine trajectory outliers from massive trajectory datasets more efficiently.The algorithm is based on space partition and finds trajectory outliers through mining the local trajectory point outlier.In this way, it converts the problem of finding trajectory to traditional outlier detection problem.In addition,a novel index structure is designed to improve the computing efficiency.Experiments show its higher efficiency and its power to find more meaningful trajectory outlier.

trajectory outlier;trajectory point;space partition;grid index tree

为了在海量轨迹数据库中高效准确地挖掘出异常轨迹，提出了基于划分的异常轨迹检测算法。该算法通过计算局部轨迹点之间的匹配程度来探测异常轨迹，将异常轨迹检测由形状匹配问题转化为传统的异常点检测问题，并设计了一种基于空间划分的网格索引结构，提高算法的运行效率。实验证明，该算法不仅具有较高的挖掘效率，而且能够检测出更具实际意义的异常轨迹。

异常轨迹；轨迹点；空间划分；网格索引树

A

TP393

10.3778/j.issn.1002-8331.1301-0243

CHEN Gang,QIAN Meng,LIU Jin.Trajectory outlier detection based on space partition.Computer Engineering and Applications,2014,50（24）：127-132.

国家自然科学基金（No.60728204/F020404）；科技重大专项经费资助（No.2013ZX04006011-102-002）。

陈刚（1984—），男，助理工程师，主要研究方向：信息可视化、数据挖掘、自动化控制；钱猛（1988—），男，助理工程师，主要研究方向：数据库、网络化控制系统；刘金（1974—），男，研究员，硕士生导师，主要研究方向：系统工程、自动化控制系统、武器预研等。E-mail：zjucg@zju.edu.cn

2013-01-22

2013-04-22

1002-8331（2014）24-0127-06

CNKI网络优先出版：2013-05-13，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130513.1601.004.html