暗物质晕普适性的数值分析

李 辉,晋 刚

(烟台大学光电信息科学技术学院,山东 烟台 264005)

暗物质晕结构的起源和演化在暗物质研究中具有非常重要的意义．随着计算机及算法的发展,暗物质晕的N体模拟在暗物质的研究中的作用日益突出．计算机模拟通常将暗物质晕视为自引力无碰撞的恒星系统,这一做法的有效性得到了广泛肯定．近年来这一研究领域的一个显著成果是它成功揭示了暗物质晕的许多分布特性,从数值计算的诸多角度看,这些性质呈现出一定程度地普适特点．

基于NFW轮廓[1-2],Moore轮廓[3]等的数值计算结果强烈暗示暗物质晕的密度轮廓呈现如下标度律:ρ∝r-r(t),其中在暗物质晕中心γ≃1～1.5而在晕的外围γ≃3～4．作为对比,Jing和Suto建议的密度轮廓模型[5]并不普适,它内部的对数斜率γ≃1.1～1.5会由于星系不同的合并历史和暗物质晕总质量的不同而变化．后续的一些工作表明暗物质晕的密度轮廓可能在晕中心附近变得比γ≃1处更浅[6],甚至有可能出现没有尖点的核[7-8]．N体数值模拟不仅提供了暗物质晕的密度轮廓,而且给出了其他2个重要性质:速度弥散和速度空间的各向异性．这2个性质[9-15]已经很好地由简单的解析结果拟合描述．

首先,有证据支持文献[16]所谓的赝相空间密度p(r)具有普适的幂律标度ρ(r)/σ3(r)∝r-ξ,其中标度指数ξ=1.875,σ2是速度弥散．已经证实ρ(r)/σ3(r)确为半径r的一个幂函数,但是最佳的速度弥散σ2应为径向速度弥散σ2．指数ξ的最佳拟合结果在不同文献中[9,17-19]并不完全一致,但都大致分布于γ=1.90±0.05到3.19±0.03的范围内．由于ρ/σ3和相空间密度具有相同量纲,ρ/σ3因而被称为赝相空间密度[20]．

其二,Hansen等[21-22]发现密度对数斜率γ(r)和速度各向异性相关联,后者可以用各向异性参数β(r)参数化．这一关联具有普适的线性关系β≈1-1.15(1-γ/6),即在大尺度结构中心附近区域γ≈1,从而β≈0(各向同性速度弥散),而在外围区域γ≈3,相应有β≈0.5．

鉴于暗物质晕在某种程度上具有以上所述的普适特征,一个值得研究的问题是考察这些普适性的根源．如果某一性质具有基本的普适性,那么将会导致对暗物质晕起源的深刻理解．因此,有必要全面考察和鉴别暗物质晕各性质的基本程度．从本文的方法论上讲,提出衡量数值特性基本程度的一个直接指标就是该性质对于数值重构和模拟计算的鲁棒性．

本文结合了前述各方面的数值结果,以金斯方程作为检验工具对比了这些“普适”性质的鲁棒性．文章首先简要回顾了整个工作框架所需理论知识,然后通过求解金斯方程对比了密度轮廓、各向异性轮廓和赝相空间密度,最后结合数值计算和分析比较结果讨论了这几种轮廓的普适性含义和鲁棒性问题．

1 一般公式

暗物质晕可以由无碰撞玻尔兹曼方程来描述:

(1)

对于球对称系统,方程可以进一步简化为金斯方程[23]:

(2)

其中:

(3)

各向异性参数[24]定义为

(4)

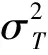
系统总动能和束缚势能为

(5)

(6)

显然,暗物质晕所对应的自引力系统中两者应满足维力定理．

2 各向异性轮廓和赝相空间密度

正如上面所提到的,暗物质晕的3个性质分别是密度轮廓、各向异性-密度关系和与速度弥散有关的赝相空间密度．如果知道其中2个,则第3个性质可以从金斯方程中计算得到．首先,在已知密度轮廓并假定各向异性轮廓的前提下通过数值求解金斯方程(2)得到速度弥散．金斯方程可以写为如下微分方程:

(7)

本文分别采用了以下几种密度轮廓．

NFW轮廓:

(8)

Moore轮廓:

(9)

Einasto轮廓[25-27]:

(10)

其中:r-2为暗物质晕半径,密度轮廓的对数斜率γ(r)=-dlnρ/dlnr取等温值,γ=2．对于NFW轮廓,rs=r-2;对于Moore轮廓,rM=22/3r-2．一些作者[27]用数值计算对比了这些轮廓,并给出了Einasto轮廓参数α的最佳拟合值为α=0.17.

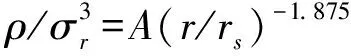
从图1中可以看到,至少在NFW和Moore模型中,赝相空间密度对各向异性轮廓并不敏感,赝相空间密度和数值计算结果相当吻合．而在Einasto轮廓中,计算结果则不是很好．维力定理的检验表明,对于这3种密度轮廓,动能束缚势能比并不敏感依赖于密度轮廓和各向异性[28]．

然后可以尝试翻转这一研究进路来考察赝相空间密度和各向异性轮廓．在求解金斯方程(2)前,先假定密度轮廓和赝相空间密度,显然可以按照上面的算法计算各向异性轮廓β．

(11)

图1 不同密度轮廓和各向异性轮廓中的赝相空间密度以及相应维力定理检验

从图2中可以看出,对于所有这3种模型,各向异性轮廓β(r)对赝相空间密度中的参数ξ都很敏感．而且,各向异性轮廓和γ之间明显偏离线性关系[27]．

3 讨 论

N体数值模拟揭示了暗物质晕的一些性质比如密度轮廓ρ(r)、各向异性参数β和赝相空间密度ρ/σ3,并且表明这些性质具有一定程度的普适性．哪一个性质更加基本呢?回答依赖于不同的数值模拟方案和衡量指标．本文从金斯方程这一角度对以上问题提供一个新的考察思路．

本文的主要计算工作和结论体现在图1和图2中．赝相空间密度对β(r)并不敏感(至少在NFW 和Moore轮廓的情况下),但是β(r)在所有情况下对赝相空间密度都很敏感,暗示赝相空间密度比各向异性轮廓更基本,这一结果再次确认赝相空间密度是解决暗物质晕起源的潜在关键．需要指出的是,图1中由金斯方程计算得到的赝相空间密度参数ξ对于NFW和Moore轮廓2种情况的结果完全一致．作为对比,各向异性轮廓β则易变且不再保持密度对数斜率参数γ的线性关系．

图2 3种轮廓中各向异性参数随赝相空间密度的变化

最后,有一些问题仍然需要加以说明并在未来进一步研究中讨论和澄清.

问题(1):在Einasto模型(α=0.17)中,采用不同的各向异性轮廓分别计算了相应的赝相空间密度．结果和数值模拟并不相符．这表明赝相空间密度ξ对β的敏感．为了得到一个符合实际的ξ值,Einasto模型的β参数需要特别指定．

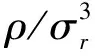
(12)

(13)

(14)

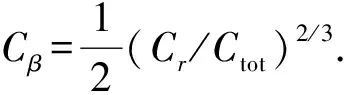
问题(3):图2中似乎各种情况的β(γ)曲线都交于一点,但真实情况并非如此．实际上那里构成的是一个区域．有趣的是,Hansen和Moore的β-γ关系也同样穿过这一区域．我们注意到在其他一些数值模拟的工作[27]中,β-γ曲线的交点在同样的区域密集分布．这似乎暗示了对这一交叠区域(β≈0.25～0.35,γ≈2.1～2.6) 进一步研究的必要性．

参考文献:

[1] Navarro J F,Frenk C S,White S D M. Simulations of X-ray clusters[J]. Royal Astronomical Society,1995,275: 720-734.

[2] Navarro J F,Frenk C S,White S D M. The Structure of cold dark matter halos[J]. Astrophysical Journal,1996,462: 563-575.

[3] Moore B,Quinn T,Governato F,et al. Cold collapse and the core catastrophe[J]. Royal Astronomical Society,1999,310: 1147-1152.

[4] Avila-Reese V,Firmani C,Klypin A,et al. Density profiles of dark matter haloes: diversity and dependence on environment[J]. Astrophysical Journal,1999,310: 527-539.

[5] Jing Y P,Suto Y. Density profiles of dark matter halo are not universal[J]. Astrophysics Journal,2000,529: L69-72.

[6] Austin C G,Williams L L R,Barnes E I,et al. Semi-analytical dark matter halos and the Jeans equation[J]. Astrophysics Journal,2005,634: 756-774.

[7] Hayashi E,Navarro J F. Hiding cusps in cores: kinematics of disk galaxies in triaxial dark matter halos [J]. Royal Astronomical Society,2006,373: 1117-1128.

[8] Tonini C,Lapi A,Salucci P. Angular momentum transfer in dark matter halos: erasing the cusp[J]. Astrophysics Journal,2006,649:591-598.

[9] Rasia E,Tormen G,Moscardini L. A dynamical model for the distribution of dark matter and gas in galaxy clusters[J]. Royal Astronomical Society,2004,351: 237-252.

[10] Dehnen W,McLaughlin D E. Dynamical insight into dark-matter haloes[J]. Royal Astronomical Society,2005,363:1057-1068.

[11] Merritt D,Graham A W,Moore B,et al. Empirical models for dark matter halos. I. nonparametric construction of density profiles and comparison with parametric models[J]. Astronomical journal,2006,132: 2685-2700.

[12] Cole S,Lacey C. The Structure of dark matter halos in hierarchical clustering models[J]. Royal Astro-nomical Society,1996,281: 716-738.

[13] Carlberg R G,Yee H K C,Ellingson E,et al. The Average mass profile of galaxy clusters[J]. Astrophysical Journal,1997,485: L13-16.

[14] Colin P,Klypin A A,Kravtsov A V,et al. Velocity bias in a LCDM model [J]. Astrophysical Journal,2000,539: 561-569.

[15] Fukushige T,Makino J. Structure of dark matter halos from hierarchical clustering[J]. Astrophysical Journal,2001,557: 533-568.

[16] Taylor J E,Navarro J F. The Phase-space density profiles of cold dark matter halos[J]. Astrophysical Journal,2001,563: 483-488.

[17] Ascasibar Y,Yepes G,Gottlober S,et al. On the physical origin of dark matter density profiles[J]. Royal Astronomical Society,2004,352: 1109-1120.

[18] Hoffman Y,Romano-Diaz E,Shlosman I,et al. Evolution of the phase-space density in dark matter halos[J]. Astrophysics Journal,2007,671:1108-1110.

[19] MacMillan J D,Widrow L M,Henriksen R N. Universal halos and the radial orbit instability [J]. Astrophysics Journal,2006,653: 43-52.

[20] Barnes E I,Williams L L R,Babul A,et al. Density profiles of collisionless equilibria. I. spherical isotropic systems[J]. Astrophysics Journal,2006,643:797-803.

[21] Hansen S H,Moore B. A universal density slope-velocity anisotropy relation for relaxed structures[J]. New Astronomy,2006,11: 333-344.

[22] Hansen S H,Stadel J. The velocity anisotropy-density slope relation[J]. Journal of Cosmology and Astroparticle Physics,2006(05): 14.

[23] Binney J,Tremaine S. Galactic Dynamics[M]. Princeton: Princeton University Press,1987.

[24] Binney J J. The radius-dependence of velocity dispersion in elliptical galaxies [J]. Royal Astronomical Society,1980,190: 873-880.

[25] Einasto J. Kinematics and dynamics of stellar systems[J]. Trudy Astrofizich-eskogo Instituta Alma-Ata,1965,51:87.

[26] Navarro J F,Hayashi E,Power C,et al. The 2dF galaxy redshift survey: Spectra and redshifts[J]. Royal Astronomical Society,2004,349: 1039-1051.

[27] Navarro J F,Ludlow A,Springel V,et al. The Diversity and similarity of simulated cold dark matter halos[J]. Astrophysics Journal,2008,689: L93-L96.

[28] He P. Entropy principle and complementary second law of thermodynamics for self-gravitating systems[J]. Royal Astronomical Society,2010,406: 2678-2688.