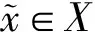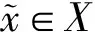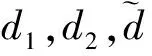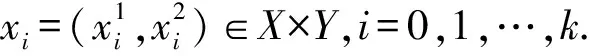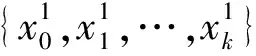两点伪轨跟踪性质与混沌
尹建东,叶 飞
(南昌大学数学系,江西 南昌 330031)
本文称(X,f)为一个紧致系统,若X为紧致度量空间,f为X上的连续自映射. 伪轨跟踪性质研究的是在一个连续自映射下的伪轨能否被跟踪的问题. 伪轨跟踪性质与系统的稳定性态和混沌性态都有着密切的联系,在动力系统的定性理论中有重要的应用. 对于伪轨跟踪性质的研究已有一系列重要成果[1-3].例如文献[1]对具有无限多个点的紧致系统,研究了伪轨跟踪性与Takens-Ruelle 意义下混沌、拓扑混合以及性质P之间的关系; 文献[2]给出了紧致空间上具有伪轨跟踪性的满射具有完全正熵的一个必要条件.文献[3]利用遍历理论讨论了具有伪轨跟踪性质系统的动力性质. 更多关于伪轨跟踪方面的研究见文献[4-6]及其中所引文献.
在文献[1-3]的基础上,引进了两点伪轨跟踪性质,并研究了具有两点伪轨跟踪性质系统的动力性状,得到一些有意思的结论.
1 预备知识

如果对于每一对非空开集U和V,都存在一个N>0,使得对任意的n>N,都有fn(U)∩V≠φ,则称f是拓扑混合的.
定义1[1]如δ>0,∀i∈Z+,0≤n1 如果对于x,y∈X,ε>0,存在X上的一个有限ε伪轨{x0,x1,…,xn},使得x0=x,xn=y,则称{x0,x1,…,xn}为一个从x到y的ε链,n+1称为该ε链的长度. 如果对任意的x,y∈X,ε>0,都存在一个从x到y的ε链,则称f是链可迁的. 如果对任意的x,y∈X,ε>0,总存在一个正整数N,使得当n≥N时,总有一个长度为n从x到y的ε链,则称f是链混合的. 定义2[7]设(Y,g)也是一个紧致系统,如果存在同胚映射h:X→Y,使得 h∘f=g∘h, 则称f和g拓扑共轭,记作f≃g. 定义3[7]设(X,f)是一个紧致系统,d是X的一个拓扑度量,X0⊂X非空,如果存在不可数集合S⊂X0,满足 我们说f在X0上是在Li-Yorke意义下混沌的.这里的S亦称作“f的混沌集”,如果f在X上混沌,简称f是Li-Yorke混沌的. 定义4[1]令ε>0,{xn1,xn1+1,…,xn2}为f的一个δ伪轨,如果存在x∈X,使得对任意的0≤i≤n2-ni,都有d(fi(x),xn1+i)<ε,则称点x相对于f—ε跟踪δ伪轨{xn1,xn1+1,…,xn2}.如果对任意的ε>0,总存在δ>0,使得f的任意一个δ伪轨总能被X中的某点相对于f—ε跟踪,则称f满足伪轨跟踪性质. 定义5[2]设x∈X,如果对任意的ε>0,存在δ>0,使得当d(x,y)<δ时,d(fn(x),fn(y))<ε对一切n∈Z+成立,则称x是f的一个稳定点.若X中每点都是稳定的,则称f点态稳定.如果X中每一点都不是f的稳定点,则称f是满足敏感依赖初始条件. 如f是拓扑传递的且满足敏感依赖于初始条件,则称f在Takens-Ruelle意义下是混沌的. 定义6[8]如果对任意ε>0,存在δ>0,使得对任意的x,y∈X,当d(x,y)<δ时,d(fn(x),fn(y))<ε,∀n∈Z+,则称f是等度连续的. 定义7 设(X,f)是一个紧致系统,如果对任给的ε>0,存在δ>0,使得对于X中的任意δ伪轨{x0,x1,…,xn},存在x∈X,使得x—ε两点跟踪{x0,x1,…,xn},即d(x,x0)<ε且d(fn(x),xn)<ε,则称f具有两点伪轨跟踪性质. 定理1 设(X,f)是一个具有两点伪轨跟踪性质的紧致系统,f是链传递的,则f是拓扑传递的. 证明设U,V是X中的非空开集,取x∈U,y∈V,则存在δ>0,使得B(x,δ)⊂U,B(y,δ)⊂V,这里 B(x,δ)={z∈X|d(x,z)<δ}, B(y,δ)={η∈X|d(y,η)<δ}, 从而 于是fm(z0)∈fm(U)∩V,因此f是拓扑传递的. 定理2 设(X,f)是一个紧致系统,f是链混合的且具有两点伪轨跟踪性质,则f是拓扑混合的. 又f是链混合的,针对上述δ,存在M>0,使得对任意的n≥M,存在从x到y的长度为n的δ伪轨{y0,y1,…,yn},其中y0=x,yn=y.由f的两点伪轨跟踪性质可知,存在x0∈X,使得 1.2.1 0 统计方法应用EpiData数据库管理软件建立数据库,应用SPSS 17.0软件进行统计分析。计数资料用构成比(%)表示,采用X2检验,检验水准α定义为0.05(双侧)。 于是fn(x0)∈fn(U)∩V,∀n≥M.因此fn(U)∩V≠φ,∀n≥M,所以f是拓扑混合的. 注:设(X,f)是一个紧致系统,因为若f是拓扑混合的,则f是Li-Yorke混沌的,f是修改的Devaney混沌的,即Takens-Ruelle混沌的[4].因此在定理2的条件下,f是Li-Yorke混沌的且在Takens-Ruelle意义下是混沌的. 定理3 设(X,f),(Y,g)是两个紧致系统,f与g拓扑共轭,则f具有两点伪轨跟踪性质蕴含g也是具有两点伪轨跟踪性质. 证明设d1,d2分别为X,Y上的度量,h是从f到g的拓扑共轭映射,即h:X→Y同胚且h∘f=g∘h.于是对任意的ε>0,存在δ>0,使得当x1,x2∈X且d1(x1,x2)<δ时,有d2(h(x1),h(x2))<ε.又f具有两点伪轨跟踪性质,针对上述δ>0,存在δ1>0,使得f的任一δ1伪轨{x0,x1,…,xn},存在x∈X满足 d1(x,x0)<δ,d(fn(x),xn)<δ. 又注意到h-1存在且为同胚映射,从而对于上述δ1,存在δ2>0,使得对任意的y1,y2∈Y,当d2(y1,y2)<δ2时,有d1(h-1(y1),h-1(y2))<δ1.下设{y0,y1,…,ym}是g的任一δ2伪轨,即 d2(g(yi),yi+1)<δ2,i=0,1,…,m-1. 则 d1(h-1(g(yi)),h-1(yi+1))=d1(f(h-1(yi)), h-1(yi+1))<δ1,i=0,1,…,m-1, 即{h-1(y0),h-1(y1),…,h-1(ym)}是f的一个δ1伪轨.由f的两点伪轨跟踪性质得,存在x∈X,使得 d1(x,h-1(y0))<δ,d(fm(x),h-1(ym))<δ. 于是 d2(h(x),y0)<ε, d2(hfm(x),ym)=d2(gm(h(x)),ym)<ε. 令y=h(x)∈Y,则y—ε两点跟踪{y0,y1,…,ym}.所以g也具有两点伪轨跟踪性质. 定理4 设(X,f),(Y,g)是两个紧致系统且均具有两点伪轨跟踪性质,则(X×Y,f×g)也具有两点伪轨跟踪性质. 即 i=0,1,…,k-1. 于是, 所以{x0,x1,…,xk}被(x,y)—ε两点跟踪.从而(X×X,f×g)具有两点伪轨跟踪性质. 推论设(X,f)是一个紧致系统,则f具有两点伪轨跟踪性质当且仅当(X×X,f×f)具有两点伪轨跟踪性质. 证明只需在定理4中令Y=X,g=f即可. 定理5 设(X,f)是一个紧致系统,如果f具有两点伪轨跟踪性质,则对任意的k∈Z+,fk具有两点伪轨跟踪性质. 证明设k>0为任一正整数.因为f具有两点伪轨跟踪性质,所以对任意的ε>0,存在δ>0,使得f的任一δ伪轨可被X中的某点—ε跟踪. 令{x0,x1,…,xn}为fk的任一δ伪轨,即 d(fk(xi),xi+1)<δ,i=0,1,…,n-1. 令yki+j=fj(xi)(0≤j 参考文献: [1] 杨润生. 伪轨跟踪与混沌[J]. 数学学报,1996,39(3):382-386. [2] 杨润生,沈苏林. 伪轨跟踪与完全正熵[J]. 数学学报,1999,42(1):99-104. [3] 杨润生. 伪轨跟踪性质与不变概率测度[J]. 数学年刊,1998,19A(1):333-361. [4] Niu Yingxuan. The average-shadowing property and strong ergodicity[J]. J Math Ana Appl,2011,376: 528-534. [5] Kwietniak D,Oprocha P. A note on the average shadowing property for expansive maps[J]. Topology and its Applications,2012,159: 19-27. [6] Subrahmonian T K,Moothathu,Oprocha P. Shadowing,entropy and minimal subsystems[J]. Monatsh Math,2013,172:357-378. [7] 周作领. 符号动力系统[M]. 上海:上海科技教育出版社,1997. [8] 周作领,尹建东,许邵元. 拓扑动力系统——从拓扑方法到遍历论方法[M]. 北京:科学出版社,2011. [9] 叶向东,黄文,邵松. 拓扑动力系统概论[M]. 北京:科学出版社,2008.
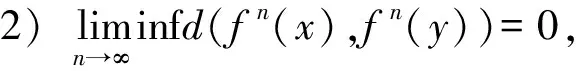
2 主要结论及证明