蚁群优化粒子滤波视觉跟踪算法

苗 彬,侯 燕

(1. 山东警察学院人事处,山东 济南 250014;2. 山东警察学院计算机系,山东 济南 250014)

视觉跟踪是计算机视觉领域的热点及难点研究内容,是实现高层次视觉行为分析的基础. 它是指对图像或视频序列中的运动目标进行检测、提取、识别和跟踪,来获得运动目标的运动参数信息,以做进一步的分析,实现对运动目标的行为理解等更高一级的视觉任务[1]. 目前,在粒子滤波算法[2-4]的框架内实现鲁棒、快速、准确的人体跟踪成为研究者关注的主要问题,这主要是由于粒子滤波算法可以有效处理复杂场景中的目标遮挡、交互等难题,从而为目标交互行为分析提供基础. 粒子滤波算法中的2个关键步骤是建议分布的设计和再采样方法的选择. 在解决不同的跟踪难题时,研究者根据目标的外观特征和动力学模型融合粒子滤波算法框架来设计不同的跟踪算法. Isard等[2]首次使用粒子滤波算法(Condensation算法)解决视觉跟踪问题,许多研究者以Condensation算法的工作为基础,提出了多种有效地处理视觉跟踪难题的改进算法. Kwon等[3]针对单目标跟踪问题,提出一种基于仿射群的粒子滤波跟踪方法. 在建立目标状态空间模型时,该算法使用仿射群作为状态,状态转移模型定义为一种几何自回归过程. 在设计建议分布时,通过将建议分布近似为高斯分布,采用局部线性化观测方程的方式,得到观测方程的一阶泰勒展开式,其思想类似于扩展卡尔曼滤波器(Extended Kalman Filter,EKF),在计算雅可比矩阵的时候,非常耗费时间. 文中提出的算法在单目标跟踪中比Condensation算法效果要好. Duffne等[4]针对考虑多种目标特征而引起的状态空间维数过高的问题,提出一种基于动态分治采样策略(DPS)的粒子滤波算法. DPS策略将高维状态空间切分成若干个子空间,每一个子空间对应一种目标特征,采样粒子时使用分层方式在各子空间中进行采样. 在子空间中采样的顺序则是根据各目标特征的可靠性来进行排序,可靠性高的先采样,以此类推. 目标特征的可靠性依据该特征从背景中区别出目标的能力进行度量. DPS-PF算法能够在复杂的场景中准确地跟踪目标,具有较好的鲁棒性. Li等[5]提出一种渐进自调整粒子滤波算法,应用于仿射群上的视觉目标跟踪. 在该算法框架中,使用尺度不变变换特征来描述目标特征,采用渐进主成分分析方法学习自适应外观子空间以产生相似性度量,实验结果证明该算法能够以较少的粒子数获得较好的鲁棒性和高精确度的跟踪结果. 文献[6]针对目标外观及姿态变化较大的目标跟踪问题,提出了基于记忆的粒子滤波算法,该算法在粒子滤波算法的框架内引入基于记忆的机制来预测先验分布,即:使用历史目标状态序列实现目标位姿和外观的同时估计. 李培华[7]提出了一种基于自适应剖分颜色空间的概率模型和推广积分图像的粒子滤波跟踪算法,旨在处理短时遮挡等难题,并取得了较好的跟踪效果. Khan等[8]基于粒子滤波算法框架,采用马尔科夫随机场运动先验模型,并结合马氏链蒙特卡罗方法,实现静态背景下的可变数目的多交互目标跟踪问题,但Khan所提出的方法仅能适用于静态背景下的跟踪问题,其实验的场景是跟踪托盘上的数只蚂蚁,具有较大的局限性.

为了解决传统的粒子滤波跟踪算法中再采样方法引起的粒子贫乏问题,提高跟踪的准确性,本文提出了蚁群优化粒子滤波跟踪算法.该算法采用蚁群优化的思想改进传统粒子滤波算法的再采样过程,从而避免样本贫乏现象引起的失跟问题,提高算法的跟踪成功率.

1 粒子滤波算法

假设k时刻系统的状态为xk,观测值序列为y1:k={y1,y2,…，yk},粒子滤波算法的基本思想是用一组由N个带权粒子构成的集合近似后验概率密度p(xk-1|y1:k-1),即:

(1)

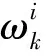
(2)

粒子滤波算法中的一个关键步骤是再采样步骤,将权值较小的粒子剔除,保留并复制权值较大的粒子,可以抑制退化现象的影响. 但是,当粒子集合中只有少数粒子权值较大时,再采样过程将仅集中到少数的粒子上,使得粒子多样性缺失,出现样本贫乏现象. 目前的解决方法是在再采样之后引入一个马氏链蒙特卡罗采样步骤,来恢复粒子多样性,但计算复杂性非常高. 本文将引入蚁群优化算法[9]的思想来取代再采样,通过模拟蚂蚁觅食路径的构建过程,来模拟粒子在状态空间中传递的过程,这样就可以避免样本贫乏现象的出现.

2 基于蚁群优化的粒子滤波算法

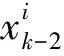
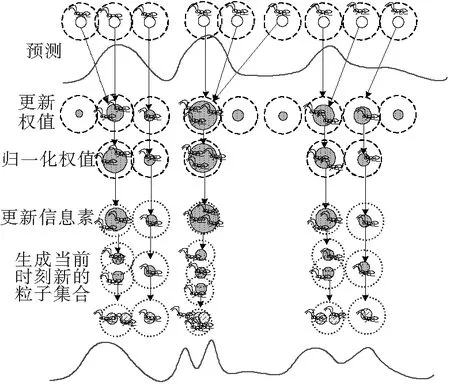
图1 基于蚁群优化的粒子滤波算法

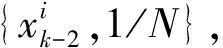
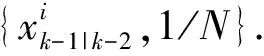
(3)

每一只蚂蚁都以一定的概率访问搜索空间中的粒子,并最终确定在下一个时刻的位置. 搜索空间中共N个粒子,但最终能吸引蚂蚁的粒子总数不一定为N,粒子的权值越大,吸引的蚂蚁就越多.

步骤3:当所有的蚂蚁全部访问搜索空间后,重新对已经聚集了蚂蚁的粒子的权值进行归一化,移除没能吸引蚂蚁的粒子.

步骤4:根据蚁群优化算法中的更新步骤,更新信息素,信息素为蚂蚁的协方差.

步骤5:根据相应的粒子生成策略得到N个k-1时刻的最终粒子,并计算系统状态估计值.

经过以上步骤之后,得到了当前时刻的粒子集合,基于该粒子集合近似后验概率密度p(xk-1|y1:k-1),然后估计当前时刻目标的位置信息.

3 实验结果及分析

本节采用5个视频序列来评价本文提出算法的性能,如表1所示. 将本文算法与基本粒子滤波算法(PF)[2]、MCMC-PF算法[8]进行对比,从定性和定量2个方面进行分析.

表1 实验视频序列

3.1 定性分析

在其中的Face序列上的跟踪结果如图2所示,从上到下依次为本文算法、PF、MCMC-PF. 结果显示本文算法能够持续准确的跟踪人脸,而其他2种算法则频繁失去人脸,MCMC-PF算法比PF稍好. 在Marry序列上的跟踪结果如图3所示,从上到下依次为本文算法、PF、MCMC-PF. 从该图可以看出,本文算法在目标发生旋转、遮挡时仍然能准确的跟踪目标,表现出较好的鲁棒性. 在其他3个序列上的跟踪结果分别如图4～6所示.

分别为第3，19，28，30帧

分别为第33，107，173，250帧

分别为第16，19，26，28，31帧

分别为第17，18，24，26帧

分别为第69，303，458，512帧

3.2 定量分析

在定量分析实验中,考察算法在5个视频序列上的跟踪成功率. 首先定义跟踪成功为:算法估计的目标区域中心与目标真实区域位置中心距离小于目标真实区域宽度的二分之一. 跟踪成功率定义为算法成功跟踪到目标的帧数与视频序列总帧数之比. 实验结果如表2所示. 本文算法在2个视频序列上的跟踪成功率为91.53%,明显高于其他2种算法.

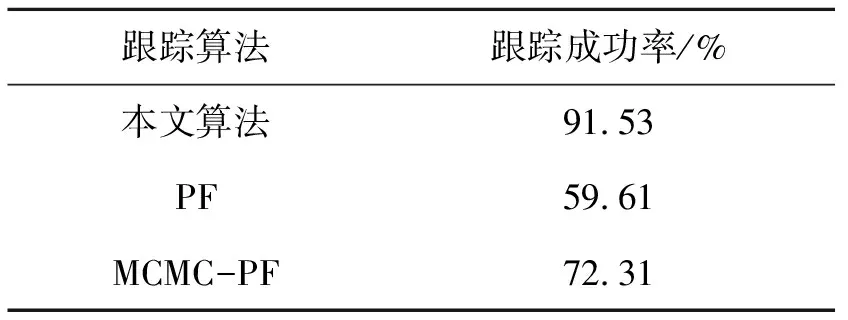
表2 算法跟踪成功率对比

4 结 论

本文提出一种基于蚁群优化方法的粒子滤波算法. 在粒子滤波算法框架内,取代传统的再采样方法,避免了样本贫乏现象的出现,在跟踪过程中可以提高算法的跟踪准确性和鲁棒性,有效处理遮挡、交互等跟踪难题. 实验结果表明本文提出的算法与传统的粒子滤波算法相比,表现出出色的跟踪性能.

参考文献:

[1] 侯志强,韩崇昭. 视觉跟踪技术综述[J]. 自动化学报,2006,32(4):603-617.

[2] Isard M,Blake A. Condensation-conditional density propagation for visual tracking[J]. International Journal of Computer Vision,1998,28(1):5-28.

[3] Kwon J,Lee K,Park F. Visual Tracking via Geometric Particle Filtering on the Affine Group with Optimal Importance Functions[C]//Proceedings of International Conference on Computer Vision and Pattern Recognition. Miami: IEEE,2009:991-998.

[4] Duffner S,Odobez J. Dynamic Partitioned Sampling for Tracking with Discriminative Features[C]//Proceedings of British Machine Vision Conference. London: BMVA,2009:710-718.

[5] Li Min,Chen Wei,Huang Kaiqi,et al. Visual Tracking via Incremental Self-tuning Particle Filtering on the Affine Group[C]//Proceedings of International Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE,2010:1315-1322.

[6] Mikami D,Otsuka K,Yamato J.Memory-based particle filter for tracking objects with large variation in pose and appearance[C]//Proceedings of European Conference on Computer Vision. Greece: Springer,2010:215-228.

[7] 李培华. 一种新颖的基于颜色信息的粒子滤波器跟踪算法[J]. 计算机学报,2009,32(12):2454-2463.

[8] Khan Z,Balch T,Dellaert F. MCMC-based particle filtering for tracking a variable number of interacting targets[J]. Pattern Analysis and Machine Intelligence,2005,27(11):1805-1819.

[9] Dorigo M,Stutzle T. 蚁群优化[M]. 北京:清华大学出版社,2007.