复杂网络中随机图模型研究

黄 斌，吴春旺，郑丰华,蔺 冰

(1.成都信息工程学院数学学院， 四川 成都 610225;2.成都信息工程学院网络工程学院，四川 成都 610225;3.成都信息工程学院计算中心和网络舆情研究所，四川 成都 610225)

1 引言

近十多年来，随着对复杂网络研究热潮的兴起，随机图成为一种重要的复杂网络模型，常常称作随机网络或随机图[1，2]。人们对复杂网络的鲁棒性、传播动力学等的研究，常常会用到随机图，即需要生成随机图模型。Erdös P和Rényi A最早研究随机图时，他们对随机图的本质做了大量的研究[3]。 随机图包含两个最基本的随机图模型[4～6]：第一种随机图模型是对给定的n个顶点的空图，任选两个顶点，两个顶点连边的概率为p所得到的一个图；而第二种随机图模型是随机选择具有M条边和n个顶点的一个图。第一种随机图模型是由Gilbert E N首先提出的[7]，而第二种随机图模型是由Erdös P和 Rényi A 提出的[4]，人们在不至于混淆的前提下，提及随机图是这两种模型中的一种。时至今日，随机图又被称为ER(Erdös-Rényi)图。自从随机图建立以来, 对随机图的研究就从未停止过，随着对随机图研究的深入，随机图的理论和应用得到极大的发展，如随机图的连通性[3]、随机图的着色[8]及色数[9，10]等等。

在复杂网络研究中，生成随机图的加边的概率小于其阈值时生成图是不连通的[3]，这对进一步研究产生了一定的困难，也不便于用随机图模仿现实中的网络，而现实世界的绝大多数网络都是连通的，如互联网、电力网、交通网等。另外，随机图模型生成算法一般都是用加边的思想[11]，而用去边的思想生成随机图的方法很少有人研究，Gilbert E N在其文章中只是一笔带过[7], 并未做进一步的研究和说明，时至今日也没有用去边的方法建立随机图模型的算法。本文基于完全图(任意两个顶点均有边相连接的简单图称为完全图，记为Kn)的生成子图的思想，给出了以去边的方式生成随机图的方法，说明用去边的方法也能够生成随机图。进一步提出生成连通图的近似随机图算法，通过数值实验验证了算法的有效性和适用性。本文所涉及的图(或网络的拓扑结构)均为：无权、无向的简单图(简单图是没有重边和环的图)。

2 去边的方式生成随机图

随机图模型对随机图理论及其应用和复杂网络的研究非常重要，以往的随机图模型的生成方式均是以加边的方式生成随机图。由于任意一个简单图都是完全图的生成子图[12]，因此可以用完全图的生成子图来构造一个新的图，即去边随机图生成算法。

2.1 算法

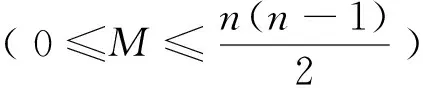
算法1去边随机图生成算法。

步骤1给定n个顶点的完全图Kn。

步骤2给定概率q, 对Kn中选定的每一条边以相同的概率q去边。

步骤3当去掉的边数达到E时就停止,E代表去掉的边数目，E=qn(n-1)/2。其中，q代表“去边”概率，p代表“加边”概率，p+q=1。

对有固定的n个节点的空图，如果以概率p随机加边，则生成的图最后有pn(n-1)/2条边；而对有n个顶点的完全图，共有n(n-1)/2条边，当以概率q去边时，共去掉qn(n-1)/2条边，此时生成子图的边的数目为：n(n-1)/2-qn(n-1)/2=(n(n-1)/2)(1-q)=pn(n-1)/2。因此,无论是加边还是去边，只要加边概率p和去边q满足：p+q=1，则生成的图，在顶点数目相同的前提下，得到的随机图的边的数目也是相同的。无论是加边还是去边均具有随机性，因此这两种方法生成的是具有相同性质的随机图。

2.2 数值实验

以“加边”的方式生成的图是随机图，如果以“去边”的方法得到的图的统计特性与“加边”的方式得到的图的统计特征完全相同，那么以“去边”的方法生成的也是随机图。在刻画随机图的统计特性上，平均聚类系数[13]、平均路径长度[14]和度分布[15]是最常用的三种参数[16]。在下面的数值实验中，计算出以这两种方法得到的图的平均路径长度、聚类系数和度分布等统计结果，以此验证 “去边”的方法得到的也是随机图。在本文的实验中，计算结果是50次实验的平均，即在相同的条件下, 对每种方法(如加边的方法)生成50个图，计算统计数值的平均值，去边也一样。

实验1取节点数目为n=3000，然后改变p、q的值，其中p代表加边概率，q代表去边概率，要求p+q=1。

从表1可以看到，这两类图的平均聚类系数、平均路径长度、平均度、最大度、最小度非常接近，其中聚类系数、平均路径长度、平均度和最大度的最大相对误差为3.7%，最小相对误差为零，对于表1最后一列的最小度，除了最小度取3和4外，其它的最大相对误差为0.86%，而最小度3和4的相对误差较大的原因是有效位数太少(表1中度的取值为整数)。另外随机性也是造成误差的原因。

Table 1 Statistical features of the two classes of graphs,fixed vertices number of the graphs are 3 000表1 两类图的统计特性，其中图的节点数目固定为3 000

注：度数取整数。

在对随机图的研究中，随机图的度分布曲线符合泊松分布是随机图的一个十分重要的标志。在接下来的实验中，比较两种不同方式得到的图(即以加边方法得到的随机图和以去边方法得到的图)的度分布曲线，说明两类图的度分布是相同的。在图1的实验中，图的节点数目仍然为n=3000，但只给出了p=0.005、q=0.995(图1a),p=0.05、q=0.95(图1b),p=0.5、q=0.5(图1c)的度分布曲线，由于其它度分布曲线结果完全类似，就没有一一给出了。

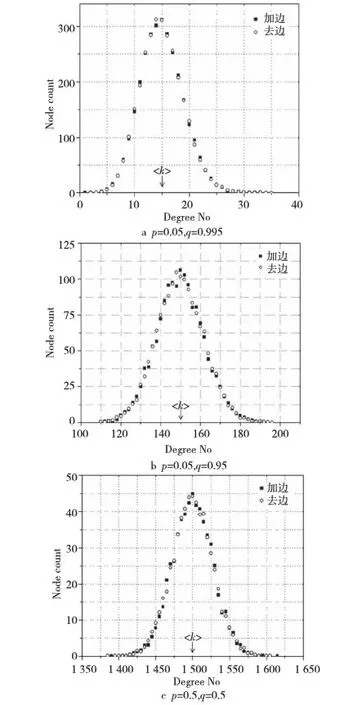
Figure 1 Degree distribution of the graphs with fixed vertices number图1 顶点数目固定图的度分布

在图1的实验中，以加边的方式得到的随机图，其度分布曲线满足泊松分布，随机图的度分布曲线在其峰值〈k〉处呈现指数下降[3,16]。而以去边的方式得到的生成子图的度分布曲线(空心圈)同样也是在其峰值〈k〉处呈现指数下降。

从以上的实验结果可以看到，在图的顶点数目不改变的前提下，改变加边和去边的概率，只要p+q=1，加边和去边的图的统计性质相同。

实验2改变生成图的节点数目，而加边概率和去边概率不变，观察两类图的统计特征。节点数目n分别取为1 000、1 500、2 000、2 500、3 500不同的值，同样p代表加边概率，q代表去边概率，要求p+q=1。

在表2的结果中，平均聚类系数和平均路径长度的最大相对误差为0.09%，最小相对误差为零；而平均度、最大度和最小度的最大相对误差为1.8%，最小相对误差同样为零。根据表2计算平均度、最大度和最小度的相对误差较大的原因，除了随机性之外，还因为度的取值为整数，使有效位数较少。因此，表2中的两类图的这些统计数值是十分接近的。

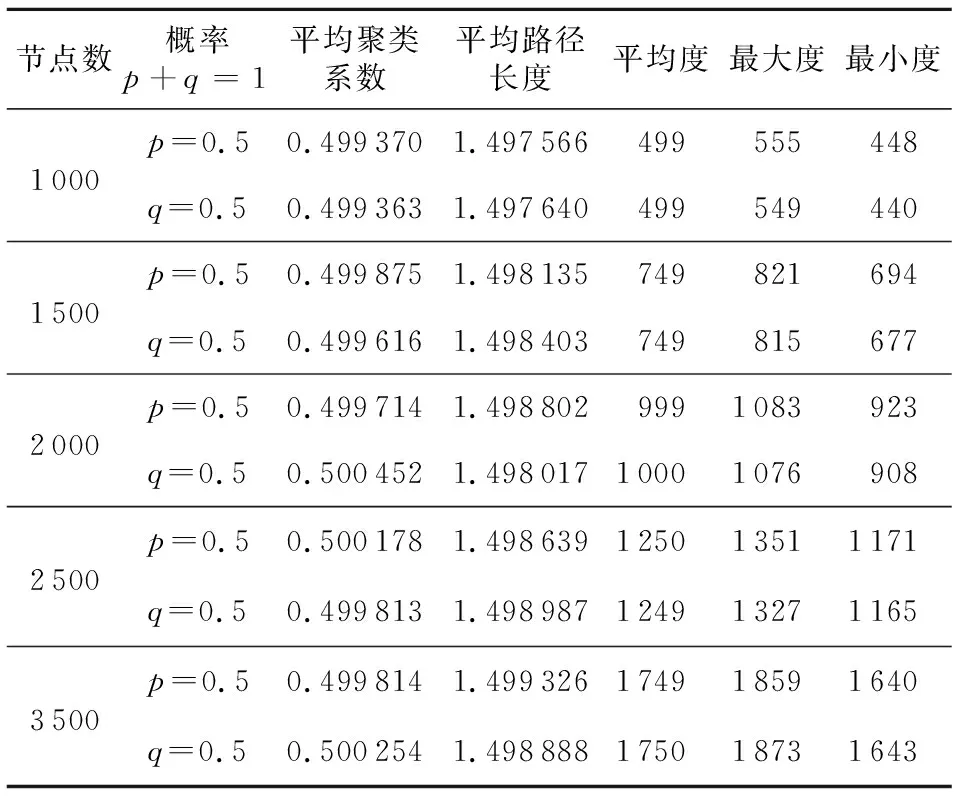
Table 2 Statistical features of the two graphs with changed vertices number表2 两类图的统计特性，其中改变图的节点数目

在图2中同样只给出了n=1000(图2a)、n=2000(图2b)、n=3500(图2c)的度分布曲线，其结果仍然是：以去边的方式得到的生成子图的度分布曲线(空心圈)与随机图一样也是在其峰值〈k〉处呈现指数下降。

Figure 2 Degree distribution of the graphs with changed vertices number图2 顶点数目改变时图的度分布

从以上实验我们可以得到如下结论：

(1)从表1和表2中都可以看出，无论是以加边方式还是去边方式所生成得到的图，其统计结果：最大度、最小度、聚集系数、平均最短路径和平均度的相对误差是很小的。

(2)图1、图2显示以这两种方法生成的图的度分布曲线均为钟型曲线，在其峰值〈k〉处呈现指数下降。

(3)在生成随机图时应该选择相对工作量较少的生成方法。以加边方式生成随机图，最终需要添加pn(n-1)/2条边。当p>0.5时，显然，用去边的方式生成的随机图，工作量更少，将更加方便和高效，反之亦然。

综上所述，可以得到如下结论：“去边随机图生成算法”也是生成随机图的一种方法。只要p+q=1,无论是以概率p加边得到的图，还是以概率q去边的方式得到的图，得到的是性质相同的图，即用“去边随机图生成算法”也可以得到随机图，这给随机图的生成方式提供了一种新的思路和算法。

3 连通随机图生成算法

复杂网络模型是研究复杂网络的基础，因此对网络模型的研究是复杂网络很重要的内容。无论是在1998年Watts D J和Strogatz S H引入了小世界网络模型，称为WS网络模型[14],还是在1999年Barabasi A L和Albert R提出了无标度网络模型，又称为BA网络模型[15]，这两种极其重要的复杂网络模型，均用到随机化的思想。在生成BA网络模型时，网络模型生成算法中，新添加的边一个端点是以一定的概率与老节点相连；而WS网络模型是使用随机化重连的思想得到的。而随机图本身也是很重要的一种复杂网络模型，人们借用随机图的生成方式可以得到随机网络模型，又称为随机图。

3.1 算法

对于随机图，当n→∞时(n为图的顶点数目)，如果加边概率p大于某个临界值pc∝lnn/n，那么几乎每一个随机图都是连通的。换言之，当连边概率p小于其临界值时，得到的图往往是不连通的[16]。在复杂网络的研究中，当想得到一个平均度为4(这是常用的复杂网络平均度)的随机网络时，无论网络的节点数目是100还是10 000，甚至节点数目更多，此时的加边概率均小于阈值pc，这时得到的往往是不连通的随机图。当连边概率p小于连通阈值pc，又希望得到连通的随机图(要求p≥2/n，当p<2/n时生成的网络始终都是不连通的)，那么目前人们的做法往往是以下三种：

(1)取不连通随机图中最大的连通分支。如在计算随机图的平均最短路径时,由于图不连通，无法计算整个随机图的平均最短路径，其中一种方法就是取整个网络中的最大连通分支的平均最短路径来代替整个随机图的平均最短路径。此方法的缺点是求解一个图的最大连通分支势必会增加运算量；同时，从网络节点数上来比较，就已经使得所选择最大连通分支与整个图必然是有差别的。

(2)多次重复：即当连边概率p较小时，生成的图不连通，就进行多次重复。每生成一个随机图，检查其连通性，若不连通，再以相同的概率再次生成一个随机图，直到生成一个连通的图为止。这种做法的缺点是显然的，因为当p很小时，重复的次数很多，甚至无法得到一个连通的图。

(3)提高连边概率p：若以概率p连边，无法得到连通的随机图，就提高p的值。如果是想得到以概率p连边的随机图，在提高p的值后，显然违背了初衷。

通过上面的分析，以上三种方法均具有明显的缺点。那么，有没有可能，以较小的概率p(p小于连通阈值)生成一个连通的随机图或者近似的随机图呢？下面就给出一个生成连通的“随机”图的算法。之所以在随机这两个字加上引号，是因为现在还无法证明它究竟有多么接近随机图。从实验数据上可以说明，以此算法生成的图一定是连通的，同时在很多性质上是接近于随机图的，特别是当p接近pc时。下面算法2的中心思想是不去掉图的割边(割边：设e1是图G的一条边，若ω(G-e1)>ω(G)，则称e1为G的割边。其中ω(G)为图G的连通分支数目，G-e1的意思是在图G中去掉边e1)，因此将此算法称为“连通随机图生成算法”。

算法2连通随机图生成算法

步骤1给定n个顶点的完全图Kn；

步骤2给定概率q,对Kn中选定的每一条边以相同的概率q去边，要求选定的边不是割边；

步骤3当去掉的边数达到E时就停止,其中E代表去掉的边数目，E=qn(n-1)/2，(其中q≤(n-2)/n)。

其中，q≤(n-2)/n，因为树是边数最少的连通图，换言之，对有n个顶点的图，只要边的数目小于n-1,则此图一定不连通[12]。任意一棵树的点边关系是：e=n-1，其中e代表的是树的边的数目，n代表的是树的顶点数目[12]。在要生成连通图的前提下，以去边的方式，所去掉的边的数目不能超过E，而E=qn(n-1)/2，故有E≤n(n-1)/2-(n-1)，又因为E=qn(n-1)/2，故q≤(n-2)/n。因为最初的完全图是连通的，当去边概率q≤(n-2)/n且去边时确保不去割边，则生成子图一定是连通的。算法2的时间复杂度是O(n4)，其中n代表图的顶点数目。

3.2 数值实验

接下来的实验中，比较加边的方式生成的随机图和去边的方法生成的随机图的连通性。

实验3取p1≈pc，其余的p2、p3、p4均小于pc(其中p1>p2>p3>p4)。

从表3可知，当pi小于pc(i=2,3,4)时，用加边的方式生成的随机图均不连通(其中不连通的结论是根据50次实验结果得到。如果超过25次生成的图均为不连通的，那么称为不连通。如果在50次的生成实验中，有大于或等于25个图是连通的，那么最终结论是连通的，见表3的最后一列)；而一切用去边的方法生成的图均为连通的，即在50次的实验中，每次得到的图均为连通的。当加边概率接近阈值pc时，以去边的方式得到的图(qi=1-pi)与加边得到的随机图在统计特性：聚类系数、平均路径长度等十分接近(参看p1、q1、p2、q2的结果)，但随着去边概率的加大，两类图统计特性的计算结果相差越来越大(参看p3、q3、p4、q4的结果)，也即在确保图的连通性的同时，损失了随机性。

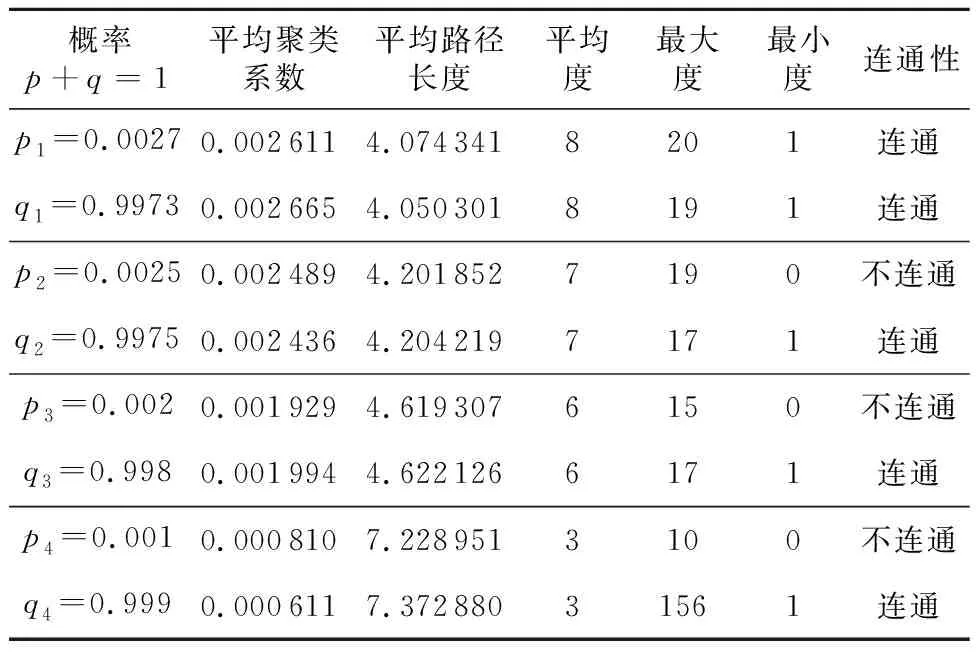
Table 3 Statistical features, when pi≤pc,qi≥qc,n=3000表3 当pi≤pc,qi≥qc时图的统计特性(n=3000)

对于度分布的实验，其中p1=0.0027,q1=0.9973(图3a),p2=0.0025,q2=0.9975(图3b),p3=0.002,q3=0.998(图3c)。

Figure 3 Degree distribution of the graphs when pi≤pc,qi≥qc图3 当pi≤pc,qi≥qc时图的度分布

在图3中，以去边的方式得到的生成子图和随机图(加边方法得到的图)一样也是在其峰值〈k〉处呈现指数下降，但当去边概率取值很大时(如：p4=0.001,q4=0.999)度分布相差较大，这里虽然没有画出图像，但从表3可以得到这一结果。

从以上实验我们可以得到如下结论：

(1)当去边概率q≤(n-2)/n时，以“连通随机图生成算法”生成的图一定连通，即用算法2生成的图一定连通。

(2)当去边概率越接近qc(qc=1-pc)时，以去边的方法得到的图的性质越接近随机图。因此，在复杂网络的研究中，如果人们希望生成一个低密度的随机图，当加边概率小于连通阈值时，得到的是不连通的图，但使用“连通随机图生成算法”，得到的一定是连通图。

(3)算法2与算法1相比较只增加了一个条件：要求选定的边不是割边。当去边概率q≤(n-2)/n时，生成子图边的数目一定大于或等于(n-1)，当满足条件后所得的图一定是连通的。

4 结束语

随机图的生成，无论对随机图理论还是复杂网络的研究，都是很重要的内容。本文基于完全图的生成子图，得到了一种生成随机图的另一种方法(算法1)，即“去边随机图生成算法”，从理论分析和具体实验都说明以去边的方式生成的图与加边的方式生成的随机图是具有相同性质的图，即都是随机图。显然这为生成随机图提供了一种新的思路和一个新的算法。如果当加边概率p>0.5时，用“去边随机图生成算法”——算法1生成随机图的效率比用以往加边的方法生成随机图的效率更高。在生成随机图时，当加边概率小于阈值pc，用加边的方法得到的随机图往往是不连通的，这对得到连通的随机图带来了极大的不便。此时如果选择不去割边的随机图生成算法，即“连通随机图生成算法”——算法2可以得到连通的近似随机图，这无疑对复杂网络的研究提供了一个新的途径。

由于任意一个静态的复杂网络的拓扑结构(无环和重边的图)都可以认为是一个完全图的生成子图，因此基于完全图的生成子图，可以得到任意一种复杂网络模型，这一工作有待进一步研究。

[1] Newman M E J. Random graphs as models of networks[M]∥Handbook of Graphs and Networks, Weinheim:Wiley, 2003.

[2] Dorogovtsev S N, Goltsev A V,Mendes J F F. Critical phenomena in complex networks[J]. Reviews of Modern Physics, 2008,80(4):1275-1335.

[3] Bollobás B. Random graphs[M].2nd ed. Cambridge:Cambridge University Press,2001.

[4] Erdös P,Rényi A.On random graphs[J]. Publicationes Mathematicae Debrecen,1959(6):290-297.

[5] Erdös P. Graph theory and probability[J]. Canadian Journal of Mathematics, 1959(11):34-38.

[6] Bollobás B. Modern graph theory[M]. New York:Springer, 1998.

[7] Gilbert E N. Random graphs[J].Ann. Math. Stat. 1959,30(4):1141-1144.

[8] Bollobás B, Thomason A G. Random graphs of small order[J].Annals of Discrete Mathematics, 1985,28:47-97.

[9] Luczak T.The chromatic number of random graphs[J]. Combinatorica, 1991,11(1):45-54.

[10] Achlioptas D,Naor A,Peres Y.Rigorous location of phase transitions in hard optimization problems[J]. Nature, 2005,435:759-764.

[11] Nobari S, Lu X, Karras P,et al. Fast random graph generation[C]∥Proc of the 14th International Conference on Extending Database Technology,2011:331-342.

[12] Zhang Xian-di, Li Zheng-liang. Graph theory and its applications[M]. Beijing:Higher Education Press, 2005. (in Chinese)

[13] Holland P W, Leinhardt S. Transitivity in structural models of small groups[J]. Comparative Group Studies, 1971,2(2):107-124.

[14] Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998(393):440-442.

[15] Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999,286(5439):509-512.

[16] Wang Xiao-fan, Li Xiang, Chen Guan-rong. Complex networks theory and its applications[M]. Beijing:Tsinghua University Press, 2006.(in Chinese)

附中文参考文献：

[12] 张先迪, 李正良. 图论及其应用[M]. 北京:高等教育出版社, 2005.

[16] 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京:清华大学出版社, 2006.