完备的双子空间边界近邻鉴别分析

林玉娥，李敬兆，梁兴柱，林玉荣

(1.安徽理工大学计算机科学与工程学院，安徽 淮南 232001;2.哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001)

1 引言

近年来，基于局部近邻思想的特征提取方法受到了学者们的关注，如局部保持投影 LPP(Locality Preserving Projections)[1]、有监督的局部保持投影LSBS(Local Structure Based Supervised)[2]、正交的保局鉴别分析OLPP(Orthogonal Locality Preserving Projections)[3]以及边界Fisher鉴别分析MFA(Marginal Fisher Analysis)[4,5]算法等，这些算法都是基于局部近邻思想提出的。其中的MFA是一种有效的特征提取算法,与其他局部近邻算法的区别是该算法综合了保局投影方法[1]和线性鉴别分析方法[6]的优点。其思想是通过构造类内图S来描述类内数据的紧致性,构造类间图B来描述类间数据的可分性,以二者的比值构造目标函数,实验表明了该算法有效性。但是，该算法也有不足之处,对此文献[7,8]指出边界Fisher鉴别分析的目标函数没有充分考虑异类样本近邻关系的缺点,因此分别提出了相应的改进算法;文献[9]则针对MFA所求的鉴别向量之间的关系进行了研究,给出了正交MFA和无相关MFA来进一步提高MFA算法的识别性能。

但是，上述改进算法和原MFA算法一样,在应用于人脸识别等模式识别问题时,均受到小样本问题的制约,即目标函数中存在矩阵奇异的问题。对于该问题目前多采用差分的目标函数来避免矩阵的求逆[10～12],这种策略虽然能够解决小样本问题,但基于差形式的目标函数的识别效果没有商形式的理想[13]。

因此，本文针对上述问题进行了研究,以MFA为理论基础,提出了一种适用于人脸识别等高维小样本问题的方法，即完备的双子空间边界近邻鉴别分析DSMNDA(Dual Subspace Marginal Neighborhood Discriminant Analysis)。 DSMNDA的思想是将MFA的目标函数分解成两部分，一部分是在边界近邻类内散度矩阵的非零空间内寻找最优投影矩阵，另一部分是在边界近邻类内散度矩阵的零空间中寻找最大化边界近邻类间散度矩阵的最佳投影矩阵。该算法的关键是求解出边界近邻类内散度矩阵的零空间与非零空间,对此本文给出了完备的求解方案,即首先要对中心化处理后的样本进行PCA降维处理,而这一过程相对于DSMNDA目标函数而言并不损失任何有效的鉴别信息, 对此给出了具体的理论证明。最后的实验结果表明了本文算法的有效性。

2 MFA 算法

设有矩阵S和B,MFA通过紧致矩阵S来描述类内数据的紧致性,即每个样本只与同类样本中的k1近邻相连；通过紧致矩阵B来描述类间数据的可分性,即只有异类样本的k2近邻相连。分别由式(1)和式(2)计算：

(1)

(2)

MFA的目标函数为:

(3)

其中，Lw=Dw-S,LB=DB-B,DW和DB都是对角矩阵,其对角元素分别为(DW)ii=∑jSij和(DB)ii=∑jBij。式(3)的求解可转换为下面的广义特征值求解问题,即:

XLwXTwi=λiXLBXTwi，i=1,2,…,l

(4)

具体求解及证明请参见文献[4,5]。

3 完备的双子空间边界近邻鉴别分析

当MFA的目标函数应用于人脸识别等高维小样本问题时,实际上并不能直接按式(4)进行分解,还要先进行PCA降维处理。但是，文献[4,5]中均没给出理论上的分析及证明,本文则对此进行了分析及证明,给出了一种完备的双子空间边界近邻鉴别分析-DSMNDA。

3.1 算法的理论推导

对于MFA的目标函数又可写成下面最大化的形式：

(5)

但是，无论是式(3)的极小化还是式(5)的最大化都存在着矩阵不可逆的问题，受文献[14]的启发,本文对此进行了分析并给出如下策略：

假设X=[x1,x2,…,xN]为高维欧氏空间Rn样本集,首先将样本中心化处理,即有:

[x1-m,x2-m,…,xN-m]

(6)

m样本的均值为向量,假设有C={n1,n2,…,nc}个类别,每类有Nl个样本,共有N个样本。定义St为总体散度矩阵,由下式计算:

(7)

因此,样本经过中心化处理后，目标函数式(5)可改写为:

(8)

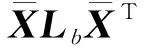
定义1设α1,α2,…,αn表示St的标准正交的特征向量集,令Z={x|Stx=0,x∈Rn},即Z为St的零空间,则有Z⊥=span{α1,α2,…,αk} (Z⊥代表Z的正交补空间),Z=span{αk+1,αk+2,…,αn}, 其中k=rank(St)。

□

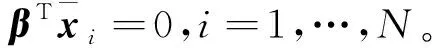
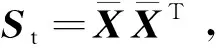
定理2对于目标函数式(8)，Z中不存有效解。

由定理1和ηr∈Z可知：

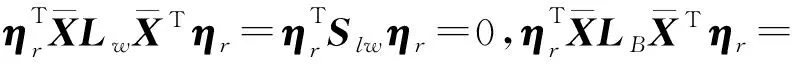
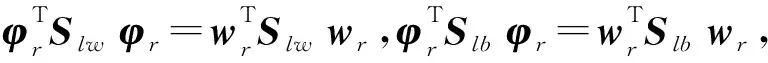
故Z中不存在式(8)的有效解。

□

由定理2可知,对于目标函数的有效解只存在于子空间Z⊥中。设:

wr=P1br

(9)

其中,P1=[α1,α2,…,αk],br∈Rk,该映射表示对于所求得的任何一个鉴别向量都是由Z⊥中的基向量线性组合生成的,则有W=P1B,B=[b1,b2,…,bl]。因此,式(8)可转换为:

(10)

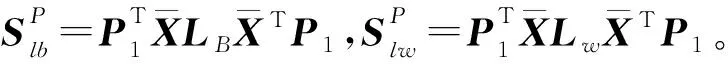
(11)

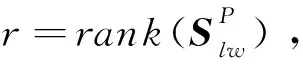
(12)

(13)

(14)

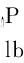
(15)

3.2 DSMNDA的具体实现

DSMNDA的具体求解步骤如下：

(1)首先根据式(7)对输入的数据进行中心化处理。

(2)对中心化后的数据根据式(1)和式(2)计算出S和B,再分别计算(DW)ii=∑jSij、(DB)ii=∑jBij、Lw=Dw-S和LB=DB-B。

(3)对St进行特征值分解,计算出St非零特征值所对应的特征向量集P1=[α1,α2,…,αk]。

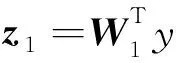
4 实验结果与讨论

为了验证所提出DSMNDA的性能,分别在FERET[15]和AR[16]人脸库上进行了测试，并采用简单的最近邻算法进行分类。FERET人脸图库,选择其一个子集来进行测试。该子集包括70人,每人6幅图像, 每幅人脸图像的尺寸为92×112。在AR人脸库选择了其中的一个子集来进行测试。该子集包括100人,每人15幅图像,每幅人脸图像的分辨率为100×80。 对于MFA和DSMNDA的近邻选择,本文选择为同类3近邻,异类为5近邻,分别进行了如下实验：

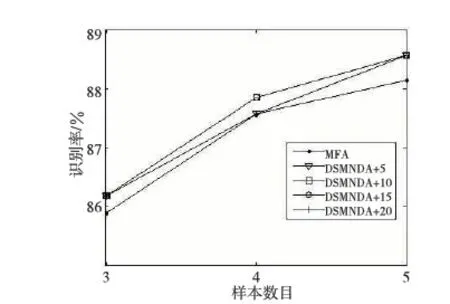
Figure 1 Performance comparisons with different samples on FERET face database 图1 FERET人脸库上不同样本下的识别结果

Figure 2 Performance comparisons with different samples on AR face database 图2 AR人脸库上不同样本下的识别结果

(2)本次实验将DSMNDA与其它的几个经典的算法进行了比较，分别是正交的LPP算法(记为ODLPP， ODLPP也加入的其所对应的零空间信息)、正交的MFA和不相关的MFA(分别记为OMFA和UMFA)。在两个人脸库上,每人随机选择T幅图像作为训练样本,T的取值为3～5,剩余图像作为测试样本。取10次平均识别结果作为每种算法的识别结果,实验结果如表1与表2所示。

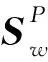
Table 1 Recognition results on FERET face database表1 FERET人脸库上的识别结果比较

Table 2 Recognition results on AR face database表2 AR人脸库上的识别结果

5 结束语

本文针对MFA算法的不足，对其进行了改进，提出一种能够有效解决小样本问题的特征提取算法，即完备的双子空间边界近邻鉴别分析——DSMNDA。该算法实质是将MFA的目标函数分解成为两部分，一部分是在类内边界近邻的零空间中求出能够最大化类间边界近邻的投影矩阵，另一部分是在类内边界近邻的非零空间求出能够同时最大化类间边界近邻且最小化的类内边界近邻的投影矩阵。对此本文给出了一种完备的求解方法,即对于目标函数中的样本,首先对中心化处理过的样本进行PCA降维,而这一过程是不损失任何有效鉴别信息的, 并给出了相应的理论证明；然后再对低维的样本进行相应的特征值分解求出两个投影矩阵，在识别阶段，只要将每个样本得到的两个特征向量串联起来形成一个向量，按最近邻方法识别即可。实验结果表明了该方法的有效性,但该方法本质上是一种线性的方法，也没有考虑样本的稀疏性，下一步我们将结合稀疏性[17]及核映射学习方法对算法进行拓展，从而进一步增强算法的识别性能。

[1] He X F, Yan S C,Hu Y.Face recognition using Laplacianfaces [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[2] Zhang H, Sun S, Jing Z, et al. Local structure based supervised feature extraction[J]. Pattern Recognition, 2006,39(8):1546-1550.

[3] Zhu L,Zhu S N. Face recognition based on orthogonal discriminant locality preserving projections[J].Neurocomputing, 2007,70(9):1543-1546.

[4] Yan S, Xu D, Zhang B, et al. Graph embedding:A general framework for dimensionality reduction [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(1):40-51.

[5] Xu D,Yan S, Tao D. Marginal fisher analysis and its variants for human gait recognition and content-based image retrieval[J].IEEE Transactions on Image Processing, 2007,16(11):2811-2821.

[6] Belhumeur P N, Hespanha J P, Kriegam D J. Eigenfaces vs. Fisherfaces:Recognition using class specific linear projection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[7] Xie Jun, Liu Jian. A new local discriminant projection method[J]. Chinese Journal of Computers,2011,31(11):2243-2250.(in Chinese)

[8] Fang B, Cheng M, Tang Y Y. Improving the discriminant ability of local margin based learning method by incorporating the global between-class separability criterion[J]. Neurocomputing,2009,73(1):536-541.

[9] Yu Yao-liang, Zhang Li-ming. Orthogonal MFA and uncorrelated MFA[J].Pattern Recognition and Artificial Intelligence,2008,21(5):604-608.(in Chinese)

[10] Lin Ke-zheng,Wang Hui-xin,Bu Xue-na.Discriminant maximum margin criterion based on locality preserving projections[J]. Pattern Recognition and Artificial Intelligence, 2010,23(2):178-185.(in Chinese)

[11] Lu Gui-fu,Lin Zhong, Jin Zhong. Face recognition based on two-dimensional maximum difference marginal fisher analysis[J]. Computer Science, 2010,35(7):251-253.(in Chinese)

[12] Lu G F, Lin Z, Jin Z. Face recognition using discriminant locality preserving projections based on maximum margin criterion [J]. Pattern Recognition, 2010,43 (3):3572-3579.

[13] Tao Y T, Yang J. Quotient vs. difference:Comparison between the two discriminant criteria [J]. Neurocomputing, 2010, 73(10-12):1808-1817.

[14] Lu Gui-fu, Lin Zhong, Jin Zhong. Optimal discriminant analysis based on kernel extension of graph embedding and face recognition[J]. Journal of Software,2011,22(7):1561-1570. (in Chinese)

[15] http://www.nist.gov/humanid/feret/feret_master.html.

[16] http://cobweb.ecn.purdue.edu/～aleix/aleix_face_DB.html.

[17] Yan De-qin, Liu Sheng-lan, Li Yan-yan. An embedding dimension reduction algorithm based on sparse analysis[J]. Acta Automatica Sinica, 2011, 37(11):1306-1312.(in Chinese)

附中文参考文献：

[7] 谢钧,刘剑.一种新的局部判别投影方法[J].计算机学报,

2011,31(11):2243-2250.

[9] 于耀亮,张立明.正交MFA和不相关MFA[J].模式识别与人工智能,2008,21(5):604-608.

[10] 林克正,王慧鑫,卜雪娜.基于局部保持投影的鉴别最大间距目标[J].模式识别与人工智能,2010,23(2):178-185.

[11] 卢桂馥,林忠,金忠.基于最大差值的二维边界Fisher的人脸识别[J].计算机科学，2010,35(7):251-253.

[14] 卢桂馥,林忠,金忠.基于核化图嵌入的最佳鉴别分析与人脸识别[J].软件学报,2011,22(7):1561-1570.

[17] 闫德勤, 刘胜蓝, 李燕燕. 一种基于稀疏嵌入分析的降维方法[J]. 自动化学报, 2011, 37(11):1306-1312.