基于改进关联分类的两次学习方法

黄再祥，周忠眉，何田中

(漳州师范学院计算机科学与工程系，福建 漳州 363000)

1 引言

对于大型数据集，构建准确而高效的分类器是数据挖掘领域的一项主要任务。1998年，Liu B等[1]提出了将关联规则和分类相结合的关联分类方法。由于关联分类具有分类准确率高和易理解等特点，一直是分类领域的研究热点之一[2～7]。

关联分类算法主要包含类关联规则产生和分类两个阶段。类关联规则是后件为类别的特殊关联规则。通常使用改进的关联规则挖掘算法来产生类关联规则，如CBA[1]使用类Apriori[8]算法，CMAR[9]使用FPgrowth[10]算法产生类关联规则。由于产生的类关联规则数量众多，大多数关联分类算法采用相关的剪枝技术，从中选出一小部分高质量的规则来构建分类器。

在分类新实例时，与待分类实例匹配的多个规则的类别经常出现不一致的情况。目前，大多数关联分类算法解决这种规则冲突问题主要有三种策略：(1)使用优先级最高的单个规则，如CBA等。(2)使用优先级最高的k个规则，如CPAR[11]等。(3)使用所有匹配的规则，如CMAR等。对于前两种方法都需要首先确定规则的优先级，而不同的优先级排序算法对分类的准确率有较大影响[12]。对于后两种方法都需要对多个规则按类别分组并计算一组规则的强度，选择强度最大的组的类别作为待分类实例的类别。不同的规则强度计算方法对分类的准确率也有较大影响。

然而，在分类某些实例时，上述处理规则冲突的策略仍然很难将这些实例正确分类。文献[13，14]等提出了一种利用神经网络解决规则冲突的方法，这种方法需要额外训练一个神经网络模型。Lindgren T等[15]提出了两次学习方法，该方法在分类实例遇到规则冲突时，从冲突规则覆盖的实例中进行第二次学习得到一组新规则来分类该实例。但是，这种方法的缺点是分类每一个实例都要进行一次学习，对大数据集来说时间开销非常大。

本文提出了基于改进的关联分类两次学习方法，创新点如下：

(1)提出改进的关联分类算法。挖掘频繁且互关联的项集用来产生规则；利用信息熵和正相关等进行剪枝；在规则排序时考虑了项集和类之间的关联程度，这样能更好地定义规则之间的优先级。

(2)提出新的两次学习框架。利用改进的关联分类算法在训练集上学习产生第一级规则；然后应用第一级规则分离出训练集中规则冲突的实例；最后，在冲突实例上应用改进的关联分类算法进行第二次学习得到第二级规则。

2 关联分类的基本概念

关联分类方法是一种使用一组关联规则来分类事务的技术。它挖掘形如X⟹Yi的类关联规则，其中X是项(或属性-值对)的集合，而Yi是类标号。假设有两个规则R1：X1⟹Y1和R2：X2⟹Y2，如果X1⊂X2，则称R1是R2的泛化规则，R2是R1的特化规则。

在关联分类中，设训练集T={t1,t2,…,tn}有m个不同的特征属性A1，A2，…,Am和一个类属性Y。如果实例ti⊇X，称之为实例ti匹配规则X⟹Yi。假设有两个规则R1：X1⟹Y1和R2：X2⟹Y2，如果ti⊇X1且ti⊇X2，Y1≠Y2，则称ti为冲突实例。

支持度和置信度是关联规则的两个重要度量。支持度(s)确定项集X可以用于给定数据集的频繁程度，而置信度(c)确定Yi在包含X的事务中出现的频繁程度。这两种度量的形式定义如下:

(1)

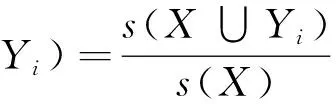
(2)

如果对于规则R：X⟹Yi，有c(X⟹Yi)>s(Yi)，这样的规则称之为正相关规则。

Omiecinski E R[16]提出了All-confidence的概念。 项集X=(a1，…,an)的All-confidence定义如下：

(3)

All-confidence代表从一个项集中抽出的所有关联规则中的最小置信度。All-confidence是衡量项集中项之间的关联程度的一种很好的度量。如果项集的All-confidence超过用户指定的阈值，则称该项集为互关联项集。All-confidence也可以用来定义规则中项集与类的关联程度，定义如下：

allconf(X⟹Yi)=s(X∪Yi)/max(s(X),s(Yi))

(4)

信息熵[17]是信息量的一种度量。项集X的信息熵E(X)定义如下：

(5)

其中,k是类标的个数，p(Yi|X)是匹配X的实例属于Yi的概率。项集信息熵越大，分类的信息量越小。因此，可以提前删除信息熵接近1的项，从而提高挖掘类关联规则的效率。

3 改进的关联分类算法

改进的关联分类算法有以下四个特点：

(1)挖掘频繁且互关联的项集。项集中项之间关联越紧密，越具有较好的分类能力。

(2)删除信息熵接近1的项，从而提高挖掘效率。项的信息熵越大，分类的信息量越小。

(3)排序。在规则排序时不仅考虑了规则的置信度和支持度，还考虑了项集和类之间的关联程度，这样能更好地定义规则之间的优先级。

(4)通过类分布的交运算计算支持度[18]，避免多次扫描数据集。在第一趟扫描过程中，记录项的类分布情况，结构如〈X,{Yi,{行号}}〉，其中X是项，Yi是类别。在随后的迭代过程中通过两个项集的类分布交运算来计算项集的支持度和置信度。例如，假设某数据集有两个类Y1和Y2，有两个项集的类分布如下：〈X1,{(Y1,{1,2,3}),(Y2,{6,7,8,9})}〉，〈X2,{(Y1,{2,3,4}),(Y2,{5,6,7,8,10})}〉。通过求交运算可得〈X1∪X2,{(Y1,{2,3}),(Y2,{6,7,8})}〉。从中可抽取规则X1∪X2⟹Y2，支持度为3，置信度为60%。

该算法的具体过程如下：

AlgorithmICAR(T,minsup,minAllconf,maxEntropy,R)

输入：训练集T，支持度阈值minsup，All-confidence阈值minAllconf，信息熵阈值maxEntropy；

输出：类关联规则集R。

1.init-pass(T,minsup,maxEntropy,L1,R);

2:for (k=2;Lk-1≠∅;k++) do

3:Ck←candidateGen(Lk-1);

4: for allXinCkdo

5: computeallconf(X);

6: ifs(X)≥minsupandallconf(X)≥minAllconfthen

7: pushXintoLk;

8: 抽取以X为前件的置信度最大的规则Ri:X→Yi;

9: ifconf(Ri)>s(Yi)

10: 在R中找出Ri的所有泛化规则；

11: if 泛化规则的置信度都小于Ri的置信度

12: pushRiintoR;

13: end if

14: end if

15: end if

16:end for

17:Sort(R);

18:DatabaseCoverage(T,R, 1);

19:returnR;

在对训练集第一趟扫描中(行1)，记录每个项出现的行号，删除信息熵超过maxEntropy的项，将频繁的项加入L1中，并抽取相应的规则放入R中。

在接下来的迭代中，类似Apriori算法，将Lk-1中的两个项集进行连接运算得到候选项集，并通过相连的两个项集的类分布的交运算计算候选项集的支持度(行3)。按公式(3)计算每个候选项集的All-confidence，将支持度和All-confidence超出相应阈值的项集X加入Lk，并抽取以X为条件的所有规则中置信度最大的规则Ri:X→Yi(行5～行8)。利用正相关性和泛化规则进行剪枝。即该规则的置信度大于相应类的支持度并且规则的置信度大于其所有泛化规则的置信度时才加入规则集(行9～行12)。候选规则产生后对规则集进行排序并利用数据库覆盖剪枝。规则按置信度、项集和类的All-confidence、项集的All-confidence、规则支持度进行排序。数据库覆盖与CMAR算法类似，选取至少能正确分类一个实例的规则，当一个实例被k个规则覆盖后将其从训练集中删除。

4 新的两次学习框架

新的两次学习框架主要有以下三个特点：

(1)利用第一级规则将训练集中的所有冲突实例分离出来。

(2)在冲突实例上进行二次学习得到第二级规则，与第一级规则共同构成分类器。

(3)基于两级规则的分类。在对一个新实例分类时，先从第一级规则集中找出与该实例匹配的优先级最高的两个规则来对该实例分类。如果匹配的两个规则预测类别不一致，则使用第二级规则集中匹配的优先级最高的规则对该实例分类。

基于改进的关联分类两次学习具体算法如下：

AlgorithmdoubleLearning(T，minsup,minAllconf,maxEntropy)

输入：训练集T，支持度阈值minsup，All-confidence阈值minAllconf，熵阈值maxEntropy;

输出：两级规则集RL1和RL2。

1.ICAR(T,minsup,minAllconf,maxEntropy,RL1);

2.ConflictSet_G(T,RL1,conflictSet);

3.ICAR(conflictSet,minsup,minAllconf,maxEntropy,RL2);

首先在训练集上利用改进的关联分类算法ICAR产生第一级规则RL1(行1)；然后利用第一级规则RL1将训练集中规则冲突的实例分离出来(行2)；最后在冲突实例集上应用相同的关联分类算法ICAR进行第二次学习得到第二级规则RL2。

冲突实例分离算法如下：

AlgorithmConflictSet_G(T,RL1,conflictSet)

输入：训练集T，第一级规则RL1;

输出：冲突实例集conflictSet。

1. for(each instancetiinT)

2. for(each ruleRiinRL1)

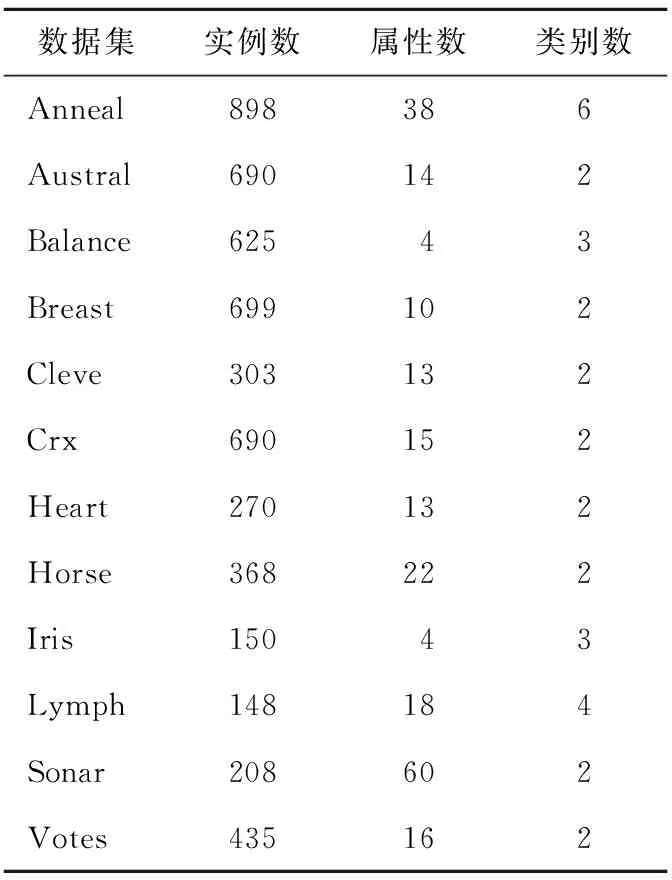
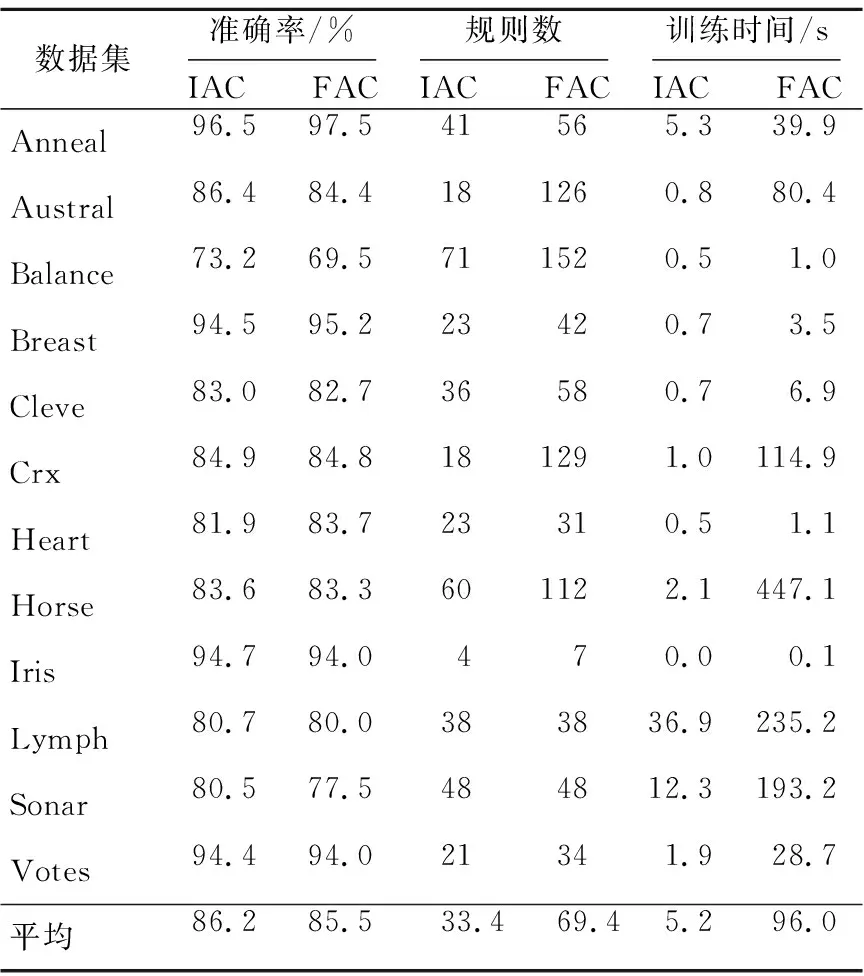
3. ifRi匹配ti&& (MR[0].conf-Ri.conf)

4. 将Ri加入匹配规则集MR;

5. end if

6. end for

7. ifMR中规则类别不一致

8. 将ti加入冲突集conflictSet;

9. end if

10. end for

利用第一级规则将冲突实例分离出来。对训练集中的每个实例从RL1中找出与第一个匹配规则置信度相差在Difconf之内的所有规则(行2～行6)，如果这些规则预测的类别不一致则将该实例加入冲突实例集(行7～行9)。

5 实验与分析

采用10-折交叉验证方法，把所有样本分成10等份，每次将其中的9份作为训练集，剩下的1份作为测试集，计算测试集的分类准确率，将10次准确率的平均值作为该数据集的准确率。我们对UCI机器学习库中的12个数据集进行了测试。这12个数据集的特征如表1所示。

Table 1 UCI dataset characteristics表1 UCI机器学习库中的数据集特征

首先，我们对改进的关联分类算法(IAC)和基于频繁的关联分类算法(FAC)的分类性能进行了比较。对于IAC, 我们将支持度、All-confidence、信息熵的阈值分别设为0.5%、10% 和0.95。对于FAC, 我们将支持度、All-confidence、信息熵的阈值分别设为0.5%、0% 和1。也就是说, FAC 近挖掘频繁项集产生规则，并且也不删除信息熵很高的项集。实验结果如表2所示。 在12个数据集中的9个数据集上，IAC取得的准确率比FAC高。此外，IAC得到的规则数减少了近一半，运行时间仅为FAC的5%。原因是频繁且互关联项集比频繁项集要少得多且这种频繁互关联项集具有更好的分类能力。

Table 2 Comparison of IAC and FAC表2 改进的关联分类与基于频繁的关联分类的比较

其次，我们对基于改进关联分类的两次学习算法(DLIAC)进行了分类性能的实验。实验结果如表3所示。

Table 3 Comparison of DLIAC and IAC表3 基于改进关联分类的两次学习算法的分类性能

实验结果表明基于改进关联分类的两次学习算法比改进关联分类算法显著提高了分类准确率，其中在Balance、Heart、Lymph、Sonar等数据集上提高了2%以上。实验结果也显示了在分类阶段一级规则冲突的实例占总的测试集的平均百分比为9%，而二级规则冲突的实例百分比显著下降到1.5%。由于两次学习需要从冲突实例中进行第二次学习，因此训练时间要稍微长一些。从表3中可以看出平均多花费大约10%的时间。

表4进一步比较了两次学习和一次学习在分类冲突实例时的准确率。冲突实例是指使用第一级规则时匹配的优先级最高的两个规则类别不一致的测试实例。一次学习采用匹配的优先级最高的规则分类冲突实例，而两次学习采用第二级规则对冲突实例分类。表3中第3列表示冲突实例在测试集中占的比例，第4列显示一次学习对冲突实例分类的准确率，第5列显示了两次学习分类冲突实例的准确率。结果显示，两次学习在分类冲突实例时显著地提高了分类准确率。

Table 4 Comparison of accuracy on conflict instances表4 分类冲突实例准确率对比

6 结束语

针对关联分类方法中规则冲突问题，本文提出了一种基于改进的关联分类两次学习方法。利用All-confidence度量项集中项之间的关联程度，挖掘频繁互关联的项集产生规则，提高规则质量。应用改进的关联分类算法在训练集上进行了两次学习得到两级规则共同构成分类器。实验结果表明，在分类冲突实例时，基于改进关联分类的两次学习方法相比一次学习算法显著提高了分类准确率。

[1] Liu B, Hsu W, Ma Y. Integrating classification and association rule mining[C]∥Proc of the 4th International Conference on Knowledge Discovery and Data Mining (KDD’98), 1998:80-86.

[2] Cheng H, Yan X, Han J, et al. Direct discriminative pattern mining for effective classification[C]∥Proc of the 20th International Conference on Knowledge Discovery and Data Mining (ICDE’08), 2008:169-178.

[3] Wu Jian-hua,Shen Jun-yi,Fang Jia-pei.An associative classification algorithm by distilling effective rules[J]. Journal of Xi’an Jiaotong University, 2009,43(4):22-25.(in Chinese)

[4] Jiang Yuan-chun, Liu Ye-zheng, Liu Xiao, et al. Integrating classification capability and reliability in associative classification:Aβ-stronger model [J]. Expert Systems with Applications, 2010, 37(5):3953-3961.

[5] Simon G, Kumar V, Li P. A simple statistical model and association rule filtering for classification[C]∥Proc of the 17th International Conference on Knowledge Discovery and Data Mining (KDD’11), 2011:823-831.

[6] Yu K, Wu X, Ding W. Causal associative classification[C]∥Proc of the 11th International Conference on Data Mining (ICDM’11), 2011:914-923.

[7] Li Xue-ming, Yang Yang, Qin Dong-xia, et al. Associative classification based on closed frequent itemsets[J]. Journal of University of Electronic Science and Technology of China,2012，41(1):104-109.(in Chinese)

[8] Agrawal R, Srikant R. Fast algorithms for mining association rules[C]∥Proc of the 20th International Conference on Very Large Data Bases (VLDB’94), 1994:487-499.

[9] Li W, Han J, Pei J. CMAR:Accurate and efficient classification based on multiple class-association rules[C]∥Proc of the 1st International Conference on Data Mining, 2001:369-376.

[10] Han J, Pei J, Yin Y. Mining frequent patterns without candidate generation[C]∥Proc of the 2000 ACM SIGMOD International Conference on Management of Data, 2000:1-12.

[11] Yin X, Han J. CPAR:Classification based on predictive association rules[C]∥Proc of the SIAM International Conference on Data Mining (SDM’03), 2003:331-335.

[12] Thabtah F.A review of associative classification mining [J]. The Knowledge Engineering Review, 2007, 22(1):37-65.

[13] Antonie M,Zaiane O,Holte R.Learning to use a learned model:A two-stage approach to classification[C]∥Proc of the 6th International Conference on Data Mining, 2006:33-42.

[14] Shekhawat P, Dhande S. A classification technique using associative classification[J]. International Journal of Computer Applications, 2011, 20(5):20-28.

[15] Lindgren T,Boström H.Resolving rule conflicts with double induction[C]∥Proc of the 5th International Symposium on Intelligent Data Analysis, 2003:60-67.

[16] Omiecinski E R. Alternative interest measures for mining associations in databases[J]. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(1):57-69.

[17] Zhao Y, Karypis G. Criterion functions for document clustering:Experiments and analysis[R]. Technical Report #01-40,Ninneapolis:University of Minnesota, 2001.

[18] Thabtah F A, Cowling P, Peng Y. MMAC:A new multi-class, multi-label associative classification approach[C]∥Proc of the 4th International Conference on Data Mining (ICDM’04), 2004:217-224.

附中文参考文献：

[3] 武建华，沈钧毅，方加沛. 提取有效规则的关联分类算法[J]. 西安交通大学学报，2009，43(4):22-25.

[7] 李学明，杨阳，秦东霞，等. 基于频繁闭项集的新关联分类算法ACCF[J]. 电子科技大学学报，2012，41(1):104-109.