基于小波变换遗传过程神经元网络的交通流预测

高 为

(广东广珠西线高速公路有限公司，广东 佛山 528305)

基于小波变换遗传过程神经元网络的交通流预测

高 为

(广东广珠西线高速公路有限公司，广东 佛山 528305)

针对短时交通流时间序列的缺点，应用小波变换理论，将含有综合信息的时间序列分离为低频确定信号和高频干扰信号，用遗传过程神经元网络分别进行预测，得到了原时间序列的实际预测结果，通过实测数据验证表明，该预测方法具有较好的预测精度。

短时交通流预测，小波变换，过程神经元网络

0 引言

智能交通系统(ITS)是近些年来热门的研究方向，而短时交通流预测是智能交通系统实现的前提和关键。由于道路交通系统是一个人、车、路、环境共同作用的复杂的非线性系统，故短时交通流具有受随机干扰因素影响大、不确定性强和规律性不明显的特点，尽管迄今为止研究了近30多种短时交通流预测方法，但仍然有很多问题亟待解决[1]。

针对短时交通流具有受随机干扰因素影响大、不确定性强和规律性不明显的特点，本文提出利用小波变换技术将短时交通流时间序列按照一定的尺度进行分解和单支重构，从而将短时交通流时间序列分离为低频确定信号和高频干扰信号，然后用遗传过程神经元网络(即用遗传算法优化过程神经元网络)分别进行预测，最后将各预测结果进行相加求和，就可得到原时间序列的实际预测结果。

1 小波变换[2]

一个能量有限信号f∈L2(R)的小波变换定义为：

(1)

(2)

这时相应的离散族为:

(3)

相应的离散小波变换为:

(4)

其重构公式为:

(5)

多尺度分析是将待处理的信号在不同的尺度上分离为低频确定信号和高频干扰信号，而小波变换则是连接不同尺度信号的纽带[3]。

给定一个尺度i及信号x(i,k)∈Vi⊂l2(Z)，k∈Z,通过一个脉冲响应为h(k)的低通滤波器，从而可以获得低频确定信号xc(i-1,k)∈Vi-1，则：

(6)

而信号x(i,k)在低通滤波器中丢失的干扰信号则可以在x(i,k)通过另一个脉冲响应为g(k)的高通滤波器得到xd(i-1,k)∈Wi-1：

(7)

(8)

式(6)和式(7)是对信号进行小波分解，而式(8)是对信号进行小波重构[4]。

2 遗传过程神经元网络

2.1 过程神经元模型

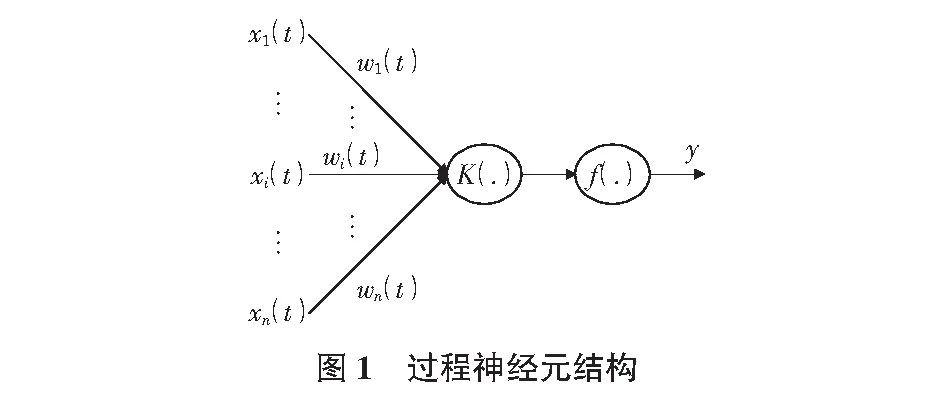
过程神经元是由加权、聚合和激励运算三部分组成，其模型结构如图1所示。图中，x1(t)，xi(t),…,xn(t)是过程神经元输入函数向量；W1(t)，Wi(t),…,Wn(t)是相应的权函数；K(.)是过程神经元的聚合基函数；f(.)是激励函数，可取线性函数、Gauss型函数、Sigrnoid函数等[5]。

其输入输出关系式为：

(9)

2.2 过程神经元网络模型

若干个过程神经元按照一定的拓扑结构组成的网络模型称为过程神经元网络模型。其模型结构如图2所示。

其输入输出关系式为：

(10)

其中，wij为输入层与隐层的连接权函数；vj为隐层过程神经元到输出层的连接权值；θj为隐层的输出阈值；[0，T]为时间采样区间。

2.3 遗传过程神经元网络模型[6,7]

遗传过程神经元网络是用遗传算法训练过程神经元网络的权值和阈值的搜索，用以克服单一过程神经元网络易陷入局部最小的缺点[8,9]。

基于遗传算法优化过程神经元网络的具体算法步骤为：

1)用某种编码方法对一权值(阈值)进行编码，随机产生一组分布，其相应对应一组过程神经元网络的连接权值(阈值)。

2)输入训练样本，计算每个个体的适应度，并以此来评价连接权(阈值)的优劣。

3)按适应度比例挑选出父本群体。

4)对父本群体进行杂交、变异操作得到新的群体。

5)重复步骤2)～4)，使初始确定的一组权值(阈值)不断进化，直到满足训练目标。

6)由遗传算法得到的次优权值再运用BP算法进行迭代训练，得到最优权值。

3 基于小波变换、遗传过程神经元网络的短时交通流预测

基于小波变换、遗传过程神经元网络的短时交通流预测模型的预测过程如图3所示。

其具体的预测过程是：

1)选择合适的小波和分解层次对实测短时交通流数据进行小波分解；

2)对分解后的各短时交通流时间序列进行单支重构；

3)对重构后各短时交通流时间序列分别进行遗传过程神经元网络的预测；

4)将各预测数据相加得到原时间序列的预测值。

4 试验结果及分析

4.1 试验数据

试验数据来源于2010年8月某城市主干路上7:00～16:00这段时间内每隔5 min的实测值，共测得108个数据。

4.2 误差指标

平均绝对相对误差：

(11)

最大绝对相对误差：

(12)

均方根误差：

(13)

其中，原数据序列为Yreal，预测结果为Ypred。

4.3 模型参数的设置

选用的小波是DB3，对短时交通流时间序列A0进行三层分解，得到4个子短时交通流时间序列，分别是：高频干扰时间序列D1～D3，低频确定时间序列A3。

遗传神经元网络设计为3层，输入层数目设为4，隐层根据实际情况和多次试验设定为10，输出层设为1，即为下一个时间间隔内的交通流。遗传算法的参数为：种群规模设置为60，交叉概率设置为0.2，变异概率设置为0.05，进化代数设置为100。

4.4 试验结果及分析

从图4中可以看出，基于小波变换、遗传过程神经元网络的预测值和实际值的变化基本相同，预测精度能满足短时交通流预测的精度范围要求。

5 结语

本文针对短时交通流具有受随机干扰因素影响大、不确定性强、规律性不明显的特点，建立了一种利用小波变换技术和遗传过程神经元网络的短时交通流预测模型，并用实测的短时交通流数据对模型进行了试验。从试验结果来看，基于小波变换、遗传过程神经元网络的短时交通流预测模型具有较好的预测精度。

[1] 陆海亭，张 宁，黄 卫.短时交通流预测方法研究进展[J].交通运输工程与信息学报，2009，7(4):84-91.

[2] TAN Manchun,LI Yingjun,XU Jianmin.A Hybrid ARIMA and SVM Model for Traffic Flow Prediction Based on Wavelet Denoising [J].Computer Engineering and Applications,2009,26(7):127-131.

[3] SkanderS.On the use of the wavelet decom position for time series prediction[J].Neurocomputing,2002(48):267-693.

[4] 贺国光，马寿峰，李 宇.基于小波分解与重构的交通流短时预测法[J].系统工程理论与实践，2002(9):101-106.

[5] 何新贵，梁久祯.过程神经元网络的若干理论问题[J].中国过程科学,2000,2(12)：40-44.

[6] 何长英.基于遗传算法的微分方程模型参数优化[J].电脑知识与技术，2005,23(18)：96-99.

[7] 刘 洁，魏连雨，杨春风.基于遗传神经网络的交通量预测[J].长安大学学报(自然科学版)，2003,23(1)：68-70.

[8] Pop R L,Paltipati K R,Bar-Shalom Y.M-best S-D assignment algorithm with application to multitarget tracing[J].IEEE Trans on AC,2001,37(1):22-38.

[9] YU B,YANG Z Z,YAO B Z.Bus arrival time prediction using support vector machines[J].Journal of Intelligent Transportation Systems,2006,11(4):151-158.

Traffic flow prediction based on wavelet transformation epigenetic process neural networks

GAO Wei

(GuangdongGuang-ZhuWestLineHighwayCo.,Ltd,Foshan528305,China)

In light of defects of short-time traffic flow time series, the paper applies wavelet transformation theory, divides comprehensive time series into low-frequency determination signal and high-frequency disturbing signal, carries out a prediction by using epigenetic process neural networks, and obtains the actual prediction results of original time series. As a result, the actual testing data proves that, the prediction method has better prediction accuracy.

short-time traffic flow prediction, wavelet transformation, process neural networks

1009-6825(2014)03-0160-03

2013-11-17

高 为(1984- )，女

U491

A