新混沌系统的有界性及其界估计
张 勇,尹社会,张光云,张付臣,袁 红
(1.河南工业职业技术学院,河南 南阳 473009;2.西南石油大学外国语学院,四川 成都 610500;3.重庆工商大学数学与统计学院,重庆 400067;4.临沂大学理学院,山东 临沂 276005)
新混沌系统的有界性及其界估计
张 勇1,尹社会1,张光云2,张付臣3,袁 红4
(1.河南工业职业技术学院,河南 南阳 473009;2.西南石油大学外国语学院,四川 成都 610500;3.重庆工商大学数学与统计学院,重庆 400067;4.临沂大学理学院,山东 临沂 276005)
借助一簇适当的Lyapunov函数和一元函数极值理论,研究了在a>k>0,b>0,c>0均为正参数情况下的一类金融混沌系统的有界性.结果表明,数值模拟与理论计算的结果相吻合.
金融混沌系统;有界性;数值仿真
一个混沌系统有界是指该系统的轨线在相空间中有界.如果可以证明一个自治混沌系统存在全局指数吸引集,那么我们可以断定在这个全局指数吸引集之外不存在该混沌系统的平衡位置、 周期解、 概周期解、 游荡回复解和其他任何混沌吸引子.俄罗斯著名学者G.A.Leonov和廖晓昕等分别研究了著名Lorenz系统的最终界和全局指数吸引集[1-2].随后,一些学者研究了其他混沌系统的有界性[3-10].我们将研究一个新金融混沌系统解的最终界,以便为该混沌系统的控制、同步提供理论依据[11].
1 数学模型
蔡国梁等[12]研究了一个改进的金融混沌系统:
(1)
其中:a>k>0,b,c为系统的正参数.当a=0.6,b=0.2,c=0.9,k=0.5,系统初值选择为(x(0),y(0),z(0))=(1,3,4)时,系统轨线的相图见图1. 取时间t=1 000 s,系统的各个变量随时间演化的波形图见图2.
有关系统(1)的一些动力学行为研究如控制和同步在文献[12]中已有报道,但是还有一些动力学行为没有涉及.我们将研究当a>k>0,b,c均为正参数时,这类系统(1)解的有界性.
2 系统解的有界性
定理1 存在正数β>0,使集合Ψ={(x,y,z)|x2+y2+(z-λ)2≤β,λ≥0}是系统(1)的最终有界和正向不变集.
证明 做广义正定、径向无界的Lyapunov函数
V(X)=V(x,y,z)=x2+y2+(z-λ)2,λ≥0.
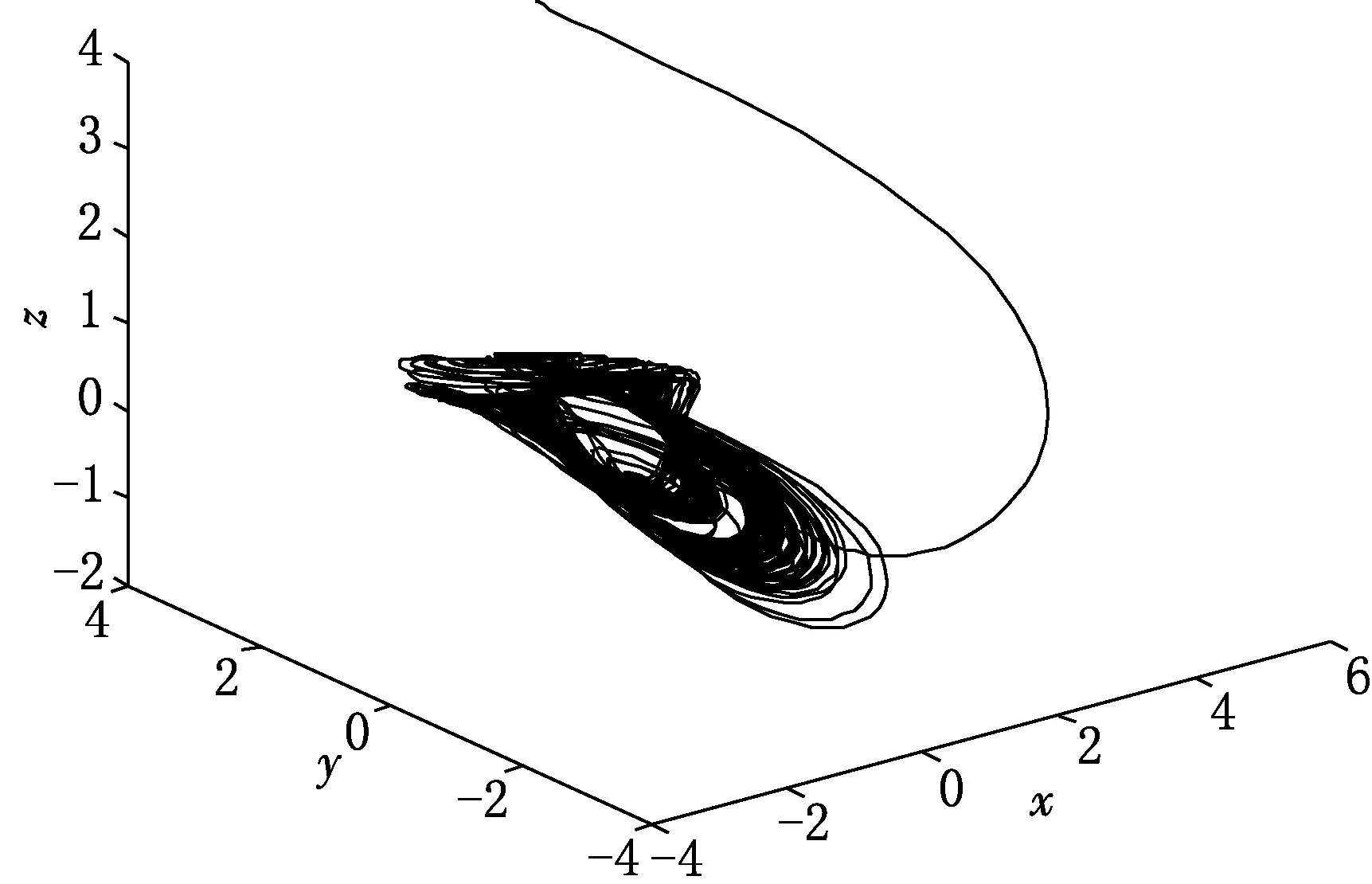
图1 系统在各个三维空间上轨线相图

图2 各个变量随时间演化的波形图
沿着系统(1)的正半轨线计算V(x,y,z)的导数,有
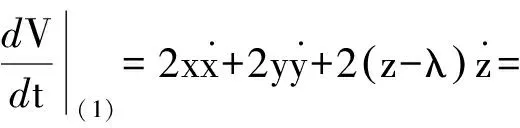
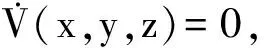
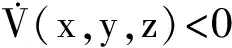
定理1虽然指出了系统(1)的正半轨线最终进入一个有界区域,即系统(1)的正半轨线是最终有界的,但是没有指出该有界区域的大小和轨线从吸引集外进入吸引集的速率估计,对于轨线从吸引集外进入吸引集的速率估计,我们有下面的定理.
定理2 令
V(X)=V(x,y,z)=x2+y2+(z-λ)2,λ≥0.
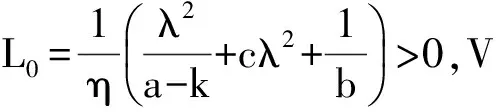
则当V(X(t))≥L0,V(X0)>L0(t≥t0)时,对于系统(1)的正半轨线,我们有指数估计式
[V(X(t))-L0]≤[V(X0)-L0]e-η(t-t0).
(2)

特别的,集合Ω={(x,y,z)|x2+y2+(z-λ)2≤L0},为系统(1)的一个全局指数吸引集.其中:
证明 做广义正定、径向无界的Lyapunov函数
V(X)=V(x,y,z)=x2+y2+(z-λ)2,λ≥0.
令
f(X)=-(a-k)x2+2λx,h(y)=-by2+2y,
(3)
当a>k>0,b>0,c>0时,经过简单计算有

沿着系统(1)的正半轨线计算V(x,y,z)的导数,当V(X(t))≥L0,V(X0)>L0时,有
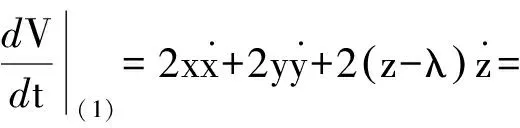
即有
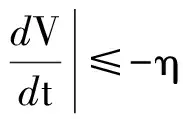
(4)
根据微分方程比较定理,当V(X(t))≥L0,V(X0)>L0(t≥t0)时,对(4)式两边积分有
V(X(t))-L0≤[V(X0)-L0]e-η(t-t0).

注记
(1) 取参数a=0.6,b=0.2,c=0.9,k=0.5,λ=0[12],这时我们有
取参数a=0.6,b=0.2,c=0.9,k=0.5,λ=1[12],这时有
由定理2,系统(1)的正半轨线包含在Ω2={(x,y,z)|x2+y2+(z-1)2≤159=(12.61)2}之中,如图4所示.

图3 系统的正半轨线包含在三维椭球Ω1内

图4 系统的正半轨线包含在三维椭球Ω2内
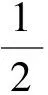
(3) 我们可以断定在全局指数吸引集Ω之外不存在金融混沌系统(1)的的平衡位置、 周期解、 概周期解、 游荡回复解和其他任何混沌吸引子.
3 结论
通过构造合适的李雅普诺夫函数簇,研究了在a>k>0,b>0,c>0均为正参数的情况下一类非线性金融系统(1)的有界性,得到了该类系统的最终界估计表达式,并且得到了轨线从吸引集外进入吸引集的速率估计式.数值模拟表明了方案的可行性.
[1] LEONOV G,BUNIN A,KOKSCH N. Attractor localization of the Lorenz system[J]. Zeitschrift Für Angewandte Mathematik Und Mechanik,1987,67:649-656.
[2] LIAO XIAOXIN. On the global basin of attraction and positively invariant set for the Lorenz chaotic system and its application in chaos control and synchronization[J]. Science in China Series E,2004,34(12):1404-1419.
[3] LI DAMEI,LU JUN AN,WU XIAOQUN. Estimating the ultimate bound and positively invariant set for the hyperchaotic Lorenz-Haken system[J]. Chaos,Solitons & Fractals,2009,39:1290 -1296.
[4] ZHANG FUCHEN,SHU YONGLU,YANG HONGLIANG. Bounds for a new chaotic system and its application in chaos synchronization[J]. Communications in Nonlinear Science and Numerical Simulation,2011,16(3):1501-1508.
[5] ZHANG FUCHEN,MU CHUNLAI,LI XIAOWU. On the boundness of some solutions of Lü system[J]. International Journal of Bifurcation and Chaos,2012,22 (1):1250015.
[6] ZHANG FUCHEN,LI YUHUAN,MU CHUNLAI. Bounds of solutions of a kind of hyper-chaotic systems and application[J]. Journal of Mathematical Research with Applications,2013,33 (3):345-352.
[7] ZHANG FUCHEN,SHU YONGLU,YANG HONGLIANG,et al. Estimating the ultimate bound and positively invariant set for a synchronous motor and its application in chaos synchronization[J]. Chaos,Solitons & Fractals,2011,44(1):137-144.
[8] ZHANG FUCHEN,MU CHUNLAI,ZHENG PAN,et al. The dynamical analysis of a new chaotic systemand simulation[J]. Mathematical Methods in the Applied Sciences,2014,37:1838-1846.
[9] WU ZHINAN,ZHANG FUCHEN,LI XIAOWU. Localization of compact invariant sets of a 4D system and its application in chaos[J]. International Journal of Research and Reviews in Applied Sciences,2012,12 (1):1-9.
[10] 张付臣,舒永录,姚宪忠. 磁盘发电机系统的动力学研究及其在混沌同步中的应用[J]. 应用数学学报,2013,36(2):193-203.
[11] 陈关荣,吕金虎. Lorenz系统簇的动力学分析、控制和同步[M]. 北京:科学出版社,2001:160-270.
[12] CAI GUOLIANG,YANG MINGZHENG. Globally exponentially attractive set and synchronization of a novel three-dimensional chaoticnance system[C]. Wuxi:Proc 3rd Int Conf Inform Comp,2010:70-73.
(责任编辑:石绍庆)
Boundedness of solutions of a novel system and simulation
ZHANG Yong1,YIN She-hui1,ZHANG Guang-yun2,ZHANG Fu-chen3,Yuan Hong4
(1.Henan Polytechnic Institute,Nanyang 473009,China;2.School of Foreign Languages,Southwest Petroleum University,Chengdu 610500,China;3.School of Mathemaitics and Statistics,Chongqing Technology and Business University,Chongqing 400067,China;4. School of Science,Linyi University,Linyi 276005,China)
The boundedness of a class of finance chaotic systems was studied via constructing a Lyapunov function and the function extreme value theory for all positive parametersa>k>0,b>0,c>0 in this paper. Numerical simulations are presented to show the effectiveness of the proposed scheme. Numerical simulation is consistent with the results of theoretical calculation.
finance chaotic system;the boundedness;numerical simulations
1000-1832(2014)04-0081-04
10.11672/dbsdzk2014-04-015
2013-08-19
重庆市自然科学基金资助项目(2009BB3185);中央高校基本科研业务费(CDJXS 10 10 00 29;CDJXS 11 10 00 26);南阳市科技发展计划项目(2013GG048);重庆市前沿与应用基础研究一般项目(cstc2014jcyjA00040).
张勇 (1981—),男,讲师,主要从事大学数学教学与研究;张付臣(1983—),男,博士,讲师,主要从事常微分方程稳定性与分岔研究.
O 415.5 [学科代码] 110·54
A

