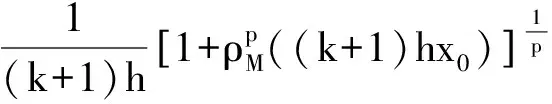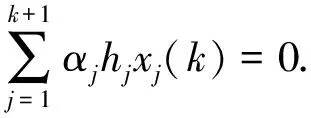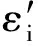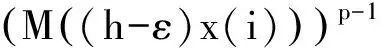赋广义Orlicz范数Orlicz序列空间的k-端点和k-强端点
张 静,段丽芬,左明霞
(1.通化师范学院数学学院,吉林 通化 134002;2.哈尔滨理工大学应用科学学院,黑龙江 哈尔滨 150080)
赋广义Orlicz范数Orlicz序列空间的k-端点和k-强端点
张 静1,段丽芬1,左明霞2
(1.通化师范学院数学学院,吉林 通化 134002;2.哈尔滨理工大学应用科学学院,黑龙江 哈尔滨 150080)
给出了由N-函数生成赋广义Orlicz范数的Orlicz序列空间中k-端点和k-强端点的判据,得到了该空间关于广义Orlicz范数k严格凸和中点局部k一致凸的条件.
广义Orlicz范数;Orlicz序列空间;k-端点;k-强端点
k-端点和k-强端点是Banach空间几何学的重要概念,它们在微分方程、逼近论、控制论等数学分支中都有应用[1-4].Orlicz空间作为一类具体的Banach空间,因为它所包含内容的丰富性和应用的广泛性,受到广大数学工作者的青睐[5-8].赋Orlicz范数和Luxemburg范数Orlicz空间的k-端点和k-强端点的判据早已获得[9-11],赋广义Orlicz范数Orlicz函数空间的k-端点和k-强端点的条件也已找到[12].本文对赋广义Orlicz范数Orlicz序列空间的k-端点和k-强端点进行了讨论,得到了由N-函数生成赋广义Orlicz范数的Orlicz序列空间中k-端点和k-强端点的判别方法,同时给出了Orlicz序列空间关于广义Orlicz范数k严格凸和中点局部k一致凸的条件.
1 预备知识
设X是Banach空间,X′表示其对偶空间,S(X)表示X的单位球面.


其中
若单位球面S(X)上每一点都是k-强端点,则称X是中点局部k一致凸的.

设p+(u)是M(u)的右导数,N(v)是M(u)的余函数,
N(v)=sup{u|v|-M(u):u≥0}.
在线性集
及其闭子空间
上赋Orlicz范数
Luxemburg范数
‖x‖M=inf{λ>0:ρM(x/λ)≤1},
及广义Orlicz范数
在Orlicz空间lM,p中,M∈Δ2指存在常数C>0和x0>0,当|x|≤x0时,满足M(2x)≤CM(x).
引理1 设M是N-函数,则对任何1 证明 按文献[13]定理4的证明过程,可得(hN,q)′=lM,p,所以对任何x=(x(i))∈lM,p,有 引理2 设M是N-函数,则对任何1 证明 首先,利用引理1 于是 且 即 由M的凸性可得,对任何i∈N, (1) 已知μ{i∈N:h0x0(i)∈RSM}≤k,不妨设{i∈N:h0x0(i)∈RSM}={1,2,…,k}.由(1)式知,当i≥k+1时有 h1x1(i)=h2x2(i)=…=hk+1xk+1(i). (2) 另外,利用Minkowsky不等式等号成立的条件,有 从而 (3) 注意到齐次线性方程组 (4) 有非零解(α1,…,αk+1).不妨设αk<0,αk+1>0,则 且当1≤i≤k-1时, 结合(3)式,可得 由于h1x1(k),h2x2(k),…,hkxk(k)在同一个线性区间上,有 (5) 类似的 若假定(5)式中不等号成立,可导出矛盾M(hkxk(k))>M(hkxk(k)),因此 考虑到h1x1(k),h2x2(k),…,hk+1xk+1(k)在同一个线性区间及0∈SM,有 结合(2),(4)两式立即可得 但 定理2 设M是N-函数,则对任何1 πM,p(α)=inf{t>0:(α+1)pM(t)·N(p+(t))>1}. 证明 必要性 假设结论不成立,则存在a∈(0,πM,p(k)),使a∉SM. 显然 (k+1)pM(a)·N(p(a))≤1. 记 b=sup{u:[(k+1)M(a)+M(u)]p-1·[(k+1)N(p+(a))+N(p+(u))]≤1}≥0, 定义 则由b的定义, 由定理1知x不是k-端点,这与lM,p(1 于是 这与由h的定义得到的结论 矛盾,因此x是k-端点.再利用定理1可得,lM,p(1 定理3 设M是N-函数,则对任何1 证明完全类似文献[11]定理2,过程冗长,略. 利用定理2和定理3,立即可得下面的结论. 定理4 设M是N-函数,则对任何1 πM,p(k)=inf{t>0:(k+1)pM(t)·N(p+(t))>1}. [1] SINGER I. On the set of best approximation of an element in a normed linear space[J]. Rev Roum Math Pure Appl,1960,5: 23-35. [2] 冼军,黎永锦,赵志红.中点局部k一致凸和Φ直和[J].中山大学学报:自然科学版,2005,17(2):251-256. [3] 倪仁兴,李冲.Banach空间中远达和同时远达问题的适定性[J].数学学报,2000,43(3):421-426. [4] 姚锋平,张克竞.二阶线性非散度型抛物方程解的局部正则性估计[J].北京大学学报:自然科学版,2011,27(2): 208-212. [5] CUI Y A,HUDZIK H,LI J J,et al. Some fundamental properties for duals of Orlicz spaces[J].Nonlinear Anal,2010,73(8): 2353-2360. [6] FORALEWSKI P,HUDZIK H,KOLWICZ P,et al. Non-squareness properties of Orlicz-Lorentz sequence spaces[J].J of Functional Anal,2013,264(2):605-629. [7] 王晓丽,吴嘎日迪,郝立宇,等.Orlicz空间中的单隐层网络逼近[J].内蒙古农业大学学报:自然科学版,2012,33(4):260-265. [8] 石忠锐,张博.广义Orlicz序列空间的非方性[J].应用数学与计算数学学报,2012,26(4):376-381. [9] 段丽芬,崔云安.Orlicz空间的k-端点和k-强端点[J].哈尔滨理工大学学报,2004,9(2): 132-134. [10] 钟坦谊,张云峰,崔云安. Orlicz序列空间的k-端点,k-光滑点[J].哈尔滨工程大学学报,1998,19(3):93-98. [11] 段丽芬,崔云安.Orlicz序列空间的k-端点和k-强端点[J].西南师范大学学报:自然科学版,2004,29(6):911-915. [12] 姜镕泽,王俊明,刘复生.赋p-Amemiya范数Orlicz空间的k-端点和k-强端点(1≤p≤∞)[J].哈尔滨理工大学学报,2011,16(2):90-93. [13] 李小彦,崔云安. 赋p-Amemiya范数Orlicz空间的对偶空间[J].哈尔滨理工大学学报,2011,16(1):110-112. (责任编辑:陶 理) k-extreme points andk-strongly extreme points in Orlicz sequence spaces endowed with the generalized Orlicz norm ZHANG Jing1,DUAN Li-fen1,ZUO Ming-xia2 (1.School of Mathematics,Tonghua Normal University,Tonghua 134002,China;2.School of Applied Sciences,Harbin University of Science and Technology,Harbin 150080,China) For the Orlicz sequence spaces generated by aN-function endowed with the generalized Orlicz Norm,criteria ofk-extreme points andk-strongly extreme points are given. And by it both sufficient and necessary conditions are presented to make them bek-rotund and mid-point locallyk-uniformly rotund. generalized Orlicz norm;Orlicz sequence space;k-extreme point;k-strongly extreme point 1000-1832(2014)04-0042-06 10.11672/dbsdzk2014-04-007 2014-03-20 国家自然科学基金资助项目(11226127);吉林省教育厅“十二五”科技项目(2014-400);黑龙江省教育厅科研项目(12531137). 张静(1978—),女,硕士,讲师,主要从事Orlicz空间几何理论研究;段丽芬(1967—),女,硕士,教授,主要从事Orlicz空间几何理论研究. O 177.3 [学科代码] 110·57 A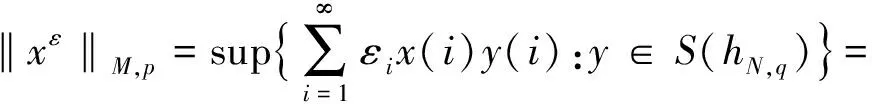
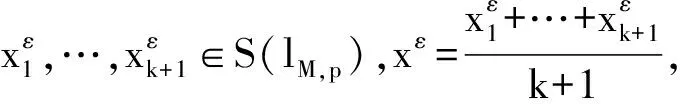

2 主要结果