高阶紧致格式在非线性数值模拟中的应用

吕 红，赵士奇，卜 忱

(1.中航工业空气动力研究院，黑龙江 哈尔滨 150001;2.中国船舶重工集团公司，北京 100097)

高阶紧致格式在非线性数值模拟中的应用

吕 红1，赵士奇2，卜 忱1

(1.中航工业空气动力研究院，黑龙江 哈尔滨 150001;2.中国船舶重工集团公司，北京 100097)

对比分析迎风型格式及中心耗散格式优劣性，采用傅里叶分析方法分析显式格式及紧致格式在波数空间可准确模拟的波数范围。通过编程研究6种紧致格式，其中为保证紧致格式在内点及边界点的一致性，采用高精度边界格式，加入了滤波运算和采用更小的CFL数来控制紧致格式的稳定性。数值试验表明，中心紧致格式有更小的耗散误差及色散误差；通过4阶Pade格式计算模型绕流，验证了边界处理的正确性，也更加认识到紧致格式有非常严格的稳定性限制。

数值模拟；高阶紧致格式；滤波运算；4阶Pade格式

0 引 言

对于一般工程问题，如海洋中船舶的绕流问题，二阶精度格式被大多数CFD应用所接受。可是由于所需求解问题日趋复杂，很多问题要求所用数值方法对流场特性有更强的模拟能力(如舰载机起飞降落和舰载机的典型机动状态的模拟),这就需要提高数值解的分辨能力，给出质量更高的流场解。解决这一问题可以通过2种方式来实现，一是通过网格技术来实现；二是建立高精度的格式。但对于舰载机等战斗机的非定常多尺度复杂流场的模拟，单利用网格技术解决该问题也存在较大困难。这就需要发展更高阶精度的格式，要求数值方法既能描述大尺度的宏观结构，又能正确反映出小尺度流动结构的影响。本文编程实现6种紧致格式，采用单波传播、单涡传播计算分析不同格式的耗散特性。数值试验表明：中心紧致格式有更小的耗散误差及色散误差。最后采用四阶Pade格式计算翼型绕流，从而验证了边界处理的正确性，也更加认识到紧致格式有非常严格的稳定性限制。

1 数值方法

曲线坐标系下的控制方程为：

(1)

(2)

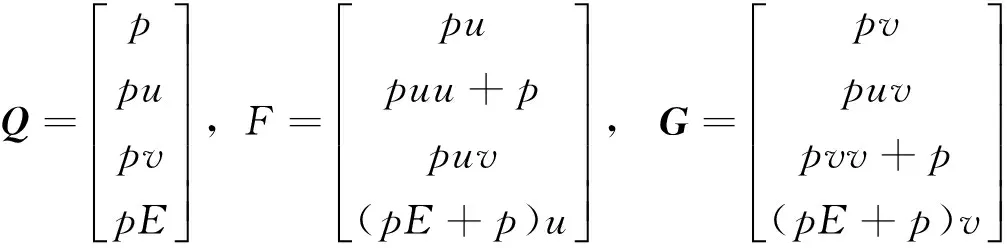
其中：

2 傅里叶分析及紧致格式

分析差分格式误差经常采用的传统方法是截断误差分析，截断误差以网格尺度为参考尺度，给出物理导数与其差分近似之间误差的量级估计。通常截断误差与流场梯度相关，表现为网格尺度的高阶小量。对于以定常、层流或湍流计算为主的传统CFD问题，流场比较光滑，二阶格式为主的低阶格式通常就足以对流场做出准确的描述，流场中存在的高波数分量往往都是需要加以抑制的数值波动。对于这样的流场，截断误差足以评价离散格式误差的影响。

在一些非定常、多尺度的计算问题中，流场中往往存在与网格尺度相当的高频分量，如大涡模拟计算中，网格尺度处于惯性子区内，因此流场中直到增大网格尺度都有比较关心的脉动量，又比如在湍流的直接模拟计算中，虽然理论上网格尺度要完全解析最小耗散尺度，然而由于所需的网格量非常大，通常只能做到使网格尺度能够精确捕捉绝大部分动能耗散，所用的网格尺度都比最小耗散尺度要大。因此，直接数值模拟计算仍然需要离散格式能够尽可能准确的捕捉与网格尺度相当的高频分量。

这要求格式不仅在物理空间有小的截断误差，还应该在波数空间较好地保持流场的频谱关系，因此需要知道格式误差在波数空间的分布及其在动力学过程中对不同波数的影响从而理解和改进数值格式处理不同波数共存的多尺度问题的能力。对这样一些问题，傅里叶分析方法是量化格式误差的有效手段。

2.1 误差分析和变形波数

通过考察变形波数可以知道差分误差在波数空间中的分布，而要了解差分误差对数值解的影响则需要考察其对差分方程动力学行为的影响。对非线性方程，其差分方程在动力学演化过程中还会产生与非线性相关联的离散误差。

用差分格式表示空间导数得到的半离散方程包含有差分误差，其动力学行为与原来的微分方程不完全一致。对半离散方程动力学行为的考察，可以揭示出差分误差对数值解产生影响的方式。

高精度差分格式的耗散特性和色散特性在数值解中表现为小尺度量的各向异性效应。这种各向异性效应既反映在波的传播特性方面，也表现在波的幅值变化方面，因此它们可能成为对所感兴趣小尺度物理量的污染源。数值解中的耗散特性可能影响小尺度量在流动中的幅值变化，色散特性可能影响小尺度量的流动结构，如改变湍流场中的拟序结构。因此，这些数值解中的高波数效应必须得到控制，使在数值模拟结果中，所感兴趣的物理量能得到正确的刻画。

变形波数的概念在差分格式误差的傅里叶分析中广泛采用，它刻画了波数空间中差分格式求得的近似导数与真实的物理导数之间的关系。对流项的逼近质量对数值解的影响极大，这里只考察1阶导数的差分格式，对应方程为:

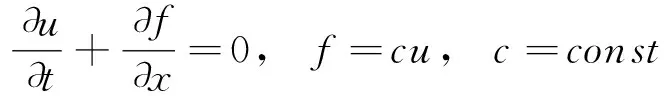
(3)

这里仅讨论初值问题。设在t=0时刻有

u(x,0)=φ(x)，

(4)

则方程(3)的解为

u(x,t)=φ(x-ct)，

(5)

为便于讨论，设方程的解具有周期性，解的定义域为[-π,π]。在这一区间分为N等分，设在t=0时刻的初始分布可通过傅里叶级数来表示：

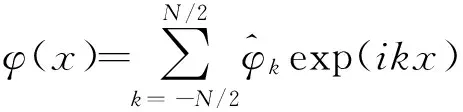
(6)

则方程(3)的解为

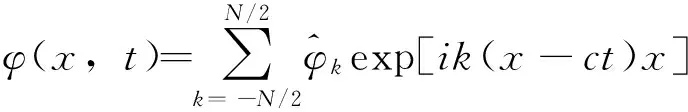
(7)

(8)

对比式(7)和式(8)可知，数值解逼近准确解要求

kr/α=0，ki/α=1，

(9)

其逼近程度反映了格式的精度，逼近方式可反映出数值解的行为特性。

这里参考LeLe对Pade格式的误差分析

(10)

(11)

在这里进行显式2阶(E2)、显式4阶(E4)、显式6阶(E6)、紧致2阶(C2)、紧致4阶(C4)、紧致6阶(C6)4种格式的傅里叶分析。

显式2阶：

ki=sin(ω)；

(12)

显式4阶：

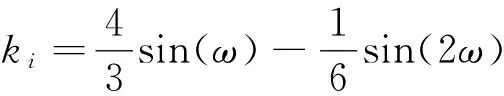
(13)

显式6阶：

(14)

紧致4阶：

(15)

紧致6阶：

(16)

图1 显式格式及紧致格式在波数空间的模拟范围Fig.1 Range simulation explicit scheme and compact format in the wavenumber space

2.2 中心型及迎风型紧致格式

空间差分格式可分为中心型和迎风型两类。中心格式采用对称模板，迎风型格式则根据特征波的传播方向，采用偏向信息来源的偏置模板。如果差分格式的模板和系数都是对称分布，则差分误差为纯粹的色散误差，相反，如果格式的模板和系数不是对称分布，则其差分误差包括耗散和色散2部分。

为了尽可能减小数值误差，提高格式对高波数分量的分辨能力，同时避免数值耗散对高波分量的影响，本文采用中心型紧致格式。紧致格式通过在一条网格线上求解代数方程组来得到变量的导数，其优点是可以在较窄的网格模板上实现较高的格式精度。通常采用的格式有求解标量三对角矩阵和标量五对角矩阵2种，因为三对角矩阵的追赶方法速度较快，为了兼顾求解效率，本文采用三对角紧致格式。

2.3 过滤运算及边界条件

对于给定的差分格式，用于数值模拟多尺度复杂流场，在网格步长确定的条件下，所能正确模拟的波数范围是一定的，超过该范围的更高波数范围的数值模拟结果是非物理的，为了消除或减小这种非物理数值结果的影响，高精度滤波方法是很有用的。

数值解中的高波数效应主要指数值误差在数值解中的反映，以及它们可能给数值解带来的影响；高波数效应具体表现为数值解中高波数的色散效应和耗散效应，对多维问题这种高波数效应还表现为色散和耗散效应在空间的各向异性特性

滤波算子应该保持低波数分量不变，并将导致奇偶失联的波长为两倍网格宽度的分量完全滤掉，因此

T(0)=1，T(π)=0，

(17)

由于滤波算子的对称性，两边Taylor展开后，奇数阶全为0，对称滤波算子，其传递函数为实数，因此滤波运算只改变不同波数分量的幅值，而不改变流场的色散关系。

滤波算子是针对计算域内点设计的，对边界点，M.R.Visbal考虑了2种处理方式：一种是仍使用对称滤波，但逐渐降低算子精度，并通过调节AF的值来改善边界滤波算子，这种方法的优点是不会带来色散误差。另一种方法是在边界点处，采用与内点具有一直精度的单侧非对称滤波算子，其优点是在边界保持高精度，缺点是会引入色散误差。考虑到滤波引入的色散误差难以控制，而逐渐降阶的方法虽然在边界处精度降低，但通过调节AF的值可以改善传递函数形状，本文采用逐渐降阶的方法。

内点的过滤运算为

(φi+n+φi-n)

边界点第3点过滤运算为

a1,3a2,3a3,3a4,3a5,3a6,3a7,3-164+af32332+13af164964+15af32516+3af8-1564+15af32332-3af16-164+af32

边界点第2点过滤运算为

a1,2a2,2a3,2a4,2a5,2a6,2a7,2116+7af834+af238+af4-14+af2116-af800

边界点处不进行滤波运算。

2.4 导数运算及边界条件

内点的求导运算为

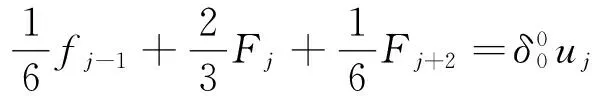
(18)

对于高阶有限差分格式，边界格式取得不好也会影响数值解的稳定性，构造与内点格式精度一致的边界格式，对于一个双曲系统，如果内点采用P阶精度的格式，则边界格式精度应达到P-1阶，才能保证空间差分离散精度为P阶。目前，许多高精度差分格式，由于未成功的构造与其精度匹配的稳定的边界格式，不得不采用低精度的边界格式，通常认为，这种情况的空间离散精度只比边界格式的精度高一阶，即高阶内点格式的精度受到边界格式的影响，而使实际计算的精度降低。

边界点的求点运算为

φ1+b2φ2+c1φ3+d1φ4)

2.5 离散方法

本文采用6种紧致格式:

Pade，经典3点4阶中心格式

(19)

OPTC4，优化5点4阶中心格式

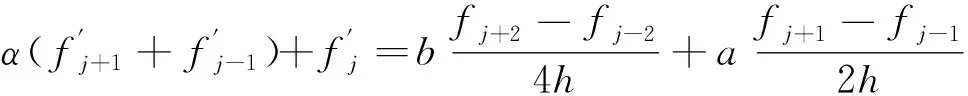
(20)

DCS5，含耗散5点中心5阶格式

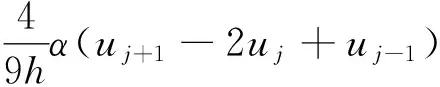
(21)

α=-0.2；

CCS6，无耗散5点中心6阶格式

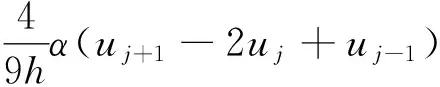
(22)

α=0；

UCD3，迎风3点3阶格式

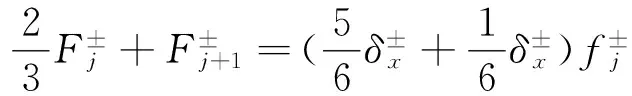
(23)

UCD5，迎风5点5阶格式

(24)

3 六种离散格式的对比分析

1)算例1 单波传播问题

u(x,0)=sin(kx)·exp[-16(x-0.5)2]，

(25)

计算区域为[0，3]，取301个计算点，取波数使得α=kΔx=2π/8≈0.79, 微分方程的解以1的速度向右传播，在T=2时，波心应到达X=2.5处。Δx=0.011，CFL=0.4，Δt=0.004，N=1/Δt=250，T=2时计算500步。

图2 六种紧致格式数值耗散对比图Fig.2 Six compact scheme numerical dissipation comparison chart

从6种紧致格式的数值试验可以看出，低阶迎风格式有太大的数值耗散，耗散中心格式比无耗散中心格式的幅值有所减小。经典4阶格式无耗散并有非常小的数值色散，接下来的工作采用的是经典4阶格式。

2)算例2 单涡传播问题

本算例模拟单涡在均匀流中的运动，主要目的是考察计算方法的数值耗散问题。计算域取为[-10,10]×[-10,10]，网格均匀分布，共包含61×61的网格点，计算域的所有边界都设定为周期性边界条件，这样涡从一个边界出去再从相反一侧的边界回到计算域中。

控制方程如下：

(26)

采用拟压缩算法，β=5.0。

初始条件，

(27)式中：P∞=0.0；U∞=1.0；R=4Δ；C=0.02RU∞。

物理时间推进采用4阶龙格库塔，时间步长Δt=0.1。

对速度及压力做数值稳定滤波，滤波算子采用F6，每个完整的龙格库塔进行一次滤波，滤波参数0.45，只滤掉了高波数分量。

计算10个周期，从计算结果看出，对2阶格式来说，涡量的耗散十分严重,高阶方法维持了涡的初始形状，没有明显耗散，4阶紧致耗散小于四阶显式格式。

图3 单涡运动云图Fig.3 Single vortex cloud

3)算例3 翼型绕流问题

计算状态：

Ma=0.3，Alf=1.25°，Re=6 000 000，CFL=0.2。

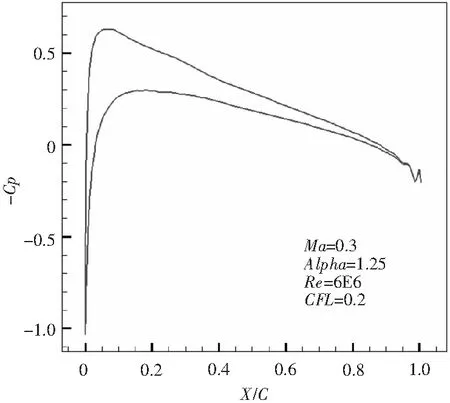
图4 压力系数分布图Fig.4 Map of the distribution of pressure coefficient

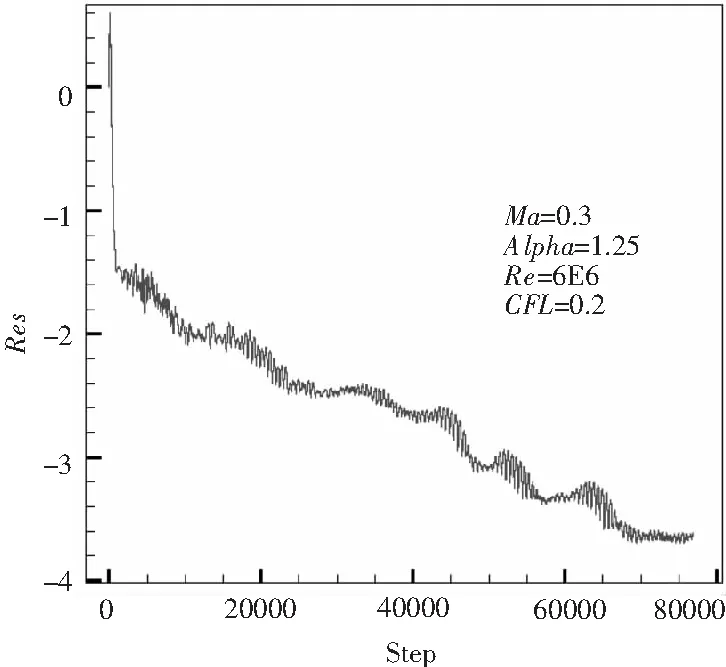
图5 残差收敛图Fig.5 Map of the residual convergence

从翼型绕流的数值试验可以看出，紧致格式有更加严格的稳定性限制，只有CFL=0.2才能保证计算收敛。

4 结 语

本文首先阐述高阶紧致格式对流动多尺度的准确模拟的重要性，对比分析了迎风型格式及中心耗

散格式优劣性，采用傅里叶分析方法分析了显式格式及紧致格式在波数空间可准确模拟的波数范围。随后，编程实现了6种紧致格式。

其中为保证紧致格式在内点及边界点的一致性，采用高精度边界格式，加入了滤波运算和采用更小的CFL数来控制紧致格式的稳定性。最后采用单波传播、单涡传播算例分析不同格式的耗散特性，数值试验表明：中心紧致格式有更小的耗散误差及色散误差；采用4阶Pade格式计算翼型绕流，从而验证了边界处理的正确性，也更加认识到紧致格式有非常严格的稳定性限制。

[1] LELE S K.Compact finite difference schemes with spectral like resolution[J].J Compt Phys,Phys,1992,103:16-42.

[2] MIGUEL R.Visbal.On the use of higher-order finite-difference schemes on curvilinear and deforming meshes[J].J Compt Phys,2002,181:155-185.

[3] 邓小刚.高阶精度耗散加权紧致非线性格式[J].中国科学，2001(12)：1104-1117.

[4] 邓小兵.不可压缩湍流大涡模拟研究[D].绵阳：中国空气动力研究与发展中心，2008.

[5] 刘昕，邓小刚，毛枚良，等.高阶精度非线性格式WCNS_E_5在二维流动中的应用研究[J].空气动力学学报，2004,22(2):206-210.

[6] 刘昕，邓小刚，毛枚良.高精度格式WCNS_E_5的Fourier分析与应用[J].应用力学学报,2006,23(3):329-333.

[7] 刘昕,邓小刚，毛枚良.高精度非线性格式WCNS的分析研究与其应用[J].计算力学学报,2007,24(3):264-268.

[8] 毛枚良，邓小刚.高阶精度线性耗散紧致格式的渐近稳定性[J].空气动力学学报,2000,18(2):165-171.

Research on application of high order compact scheme in numerical simulation of nonlinear

LV Hong1,ZHAO Shi-qi2,BU Chen1

(1.Avic Aerodynamics Research Institute,Harbin 150001,China;2.China Shipbuilding Industry Corporation,Beijing 100097,China)

The article analyzed the merits of the upwind scheme and central dissipation scheme. Using the Fourier analysis method to analyze the wave number range of explicit and compact format, it can be accurately simulated in wave number space. Through programming on six compact scheme, In order to ensure consistency of formats, including compact point and boundary points, the program use high-precision format border. Filtering operation and the use of a smaller number of CFL compact format to control the stability. Numerical experiments show:the centre compact format has smaller error of dissipation and dispersion. Through fourth-order Pade format to compute the flow around airfoil, It verifies the correctness of the boundary treatment. Morely, we recognize the compact scheme has very strict stability limit.

numerical simulation;advanced compact scheme;filtering operation;fourth-order pade format

2014-03-01;

2014-06-25

总装备部重点预研基金资助项目

吕红(1981-)，女，高级工程师，研究方向为流体力学。

V211.1+5

A

1672-7649(2014)11-0085-06

10.3404/j.issn.1672-7649.2014.11.017