破损舰船在波浪中的响应预报与试验研究

冯乾栋，胡嘉骏，张 凡，耿彦超

(中国船舶科学研究中心，江苏 无锡 214082)

破损舰船在波浪中的响应预报与试验研究

冯乾栋，胡嘉骏，张 凡，耿彦超

(中国船舶科学研究中心，江苏 无锡 214082)

为研究舰船破损后在波浪中的响应，开展舰船在完整正浮状态以及破损后倾斜状态的模型试验。基于三维线性势流理论，使用三维频域方法对模型破损前后的响应做数值预报。与试验结果相比，数值预报结果符合较好，验证了预报方法的合理性。最后，通过与该舰船模型破损前的响应结果对比，研究分析破损对舰船在波浪中响应的影响。

破损舰船；模型试验；三维频域方法

0 引 言

虽然航海技术不断进步，由于搁浅、碰撞等意外情况，舰船仍然难免面临着出现结构破损导致海水淹舱的危险。船舶破损舱室进水后，船身不仅吃水增加，并且会失去正浮产生倾斜，如果再遭遇恶劣海况，船身结构极可能会进一步破损，从而造成海难。因此，对于舰船破损后在波浪中的响应研究很有现实意义。

自从“爱沙尼亚”号滚装船海难后，不少国外学者对舰船破损后的响应预报以及试验展开研究。Emin Korkut等[1-2]分别制作了完整以及破损的滚装船模型，通过水池试验比较了滚装船破损前后的运动响应与波浪载荷。Chan等[3-4]使用二维切片理论，在时域内考虑了船体大幅值运动时剧烈变化的湿表面影响，预报了破损滚装船在规则斜浪中的非线性运动与波浪载荷。Lee等[5]考虑船体多种破损情况，使用了源汇分布法求解了破损后非对称剖面的二维辐射和绕射流场，利用线性切片理论预报了船舶破损后的波浪载荷，并展开了模型试验与数值预报做了对比。

在国内，吴明远、青兆熹[6-7]采用三维方法在频域内计算了船体周围的速度势分布，预报了船舶横倾后的6自由度运动与波浪载荷。这些研究都获得了有益的结果，但是都尚未开展模型试验，其理论预报结果缺乏模型试验的验证。

本文通过开展模型试验与数值预报，研究舰船发生第一类舱室破损，由舱室淹水导致的船身倾斜与吃水增加对船体运动与波浪载荷的影响。在模型试验方面，本文分别开展完整正浮与破损后横倾的舰船模型对比试验，测量该模型在2种状态下在顶浪规则波中的响应。另外，本文基于三维势流理论，使用三维奇点分布法求解非定常流场，进而对模型的运动响应与波浪载荷进行数值预报，并将数值预报同模型试验结果进行比较验证。

1 破损舰船三维线性频域预报方法

1.1 三维速度势求解

(1)

式中：ωe为遭遇频率；n为船体表面单位法矢量，在细长船体假设下，本文取简化形式的mj，即(m1,m2,m3)=(0,0,0)， (m4,m5,m6)=(0,n3,-n2)。

(2)

通过简化，带有航速的自由面条件与零航速情况形式相同，只需以遭遇频率ωE代替自然频率ω，从而使得有航速速度势的求解可转换为零航速问题。

简化后的船体三维速度势可以通过三维奇点分布法来求解：采用面元法将连续物面(船体平均湿表面)离散，使用零航速的三维自由面Green函数建立分布源方程组，求解得到面元中心处的源强与Green函数后，使用分布源积分方法即可求解出船体周围的三维速度势。

1.2 破损舰船在规则波中的运动与波浪载荷计算

假设舰船发生第一类舱室破损，即舱的顶部位于水线以下，船体破损后海水灌满整个舱室，因此本文不考虑淹舱水晃荡对于船体运动与载荷的影响。

(3)

式中，η为船体的稳态运动响应；M为质量矩阵；C为静水回复力矩阵；A和B分别为附加质量矩阵以及附加阻尼矩阵；fw为波浪激励力。

由于船舶破损后具有一定横倾，船体质量分布、静水浮力不再关于中纵剖面对称，所以破损船运动方程中的质量矩阵M与静水回复力矩阵C与破损前有所不同。

(4)

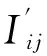
完好的船舶由于水线面左右对称，静水恢复矩阵中有5项不为0，而非正浮破损船的水线面不再对称，其静水回复力矩阵C中有9项不为0：

(5)

式中：Awp为水线面面积;Sx为水面线对x轴的静矩;Sy为水面线对y轴的静矩；Jxy为水面线对原点的静矩;hx为横稳性高;hy为纵稳性高。

通过式(3)求解得到六自由度运动后，船中剖面处的波浪载荷Q可以通过下式计算：

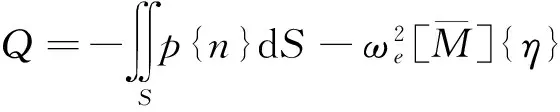
(6)

式中p为各面元处的脉动压力。

2 船模试验

本文分别对完整正浮与破损后横倾的舰船模型进行了试验，测量了该模型2种状态下在顶浪规则波中的响应。船模试验在中国船舶科学研究中心05耐波性水池中进行，该水池长69 m,宽46 m，水深4 m，在长、短两边布置有摇板式造波机。试验采用某深V型舰船模型，其主要参数如表1所示。模型为分段龙骨梁型玻璃钢自航船模，共分4段，用测量梁连接。

表1 船模主要参数Tab.1 Principal dimensions of ship model

为了开展破损后横倾的船体模型试验，本次试验通过使用压载来模拟舰船2处破损后的淹舱水。在重心前后60 cm处分别放置7 kg压载，其在横剖面内的位置如图1所示，测得船体产生横倾7.8°(左倾)。图2为水池中的试验模型。

试验都在规则波中进行，波高取82.5 mm，使用的波长范围：λ/L=0.4～2.5， 船模航速V=0，0.813 m/s，对应的Fr=0，0.128。在船模重心处放置陀螺仪，用于测量船体垂荡与纵摇响应。在水池测量小车上，位于模型前约1.5 m处安装1台伺服式浪高仪，用来测量试验时模型遭遇的波浪。

图1 压载在横剖面内的位置Fig.1 Position of load in crosssection

图2 水池中的试验模型Fig.2 Test model in the pool

3 破损前后响应对比分析

根据三维线性频域理论对该船模破损前后在规则波中的响应进行计算，并与试验结果比较分析。图3和图4分别为破损前后的纵摇、垂荡响应，图5为破损前后的垂向波浪弯矩。

图3 纵摇RAO比较Fig.3 Comparison of pitch′s RAO

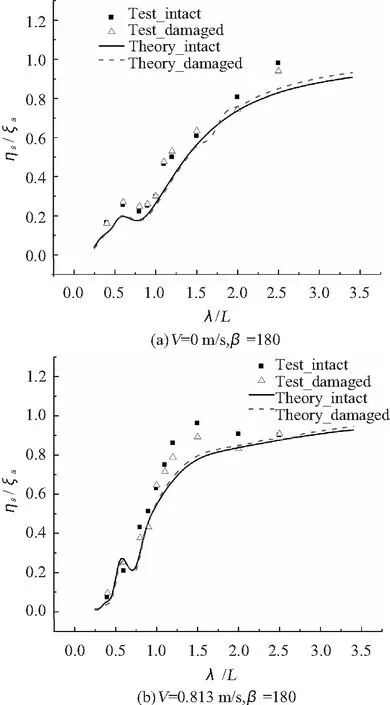
图4 垂荡RAO比较Fig.4 Comparison of heave′s RAO

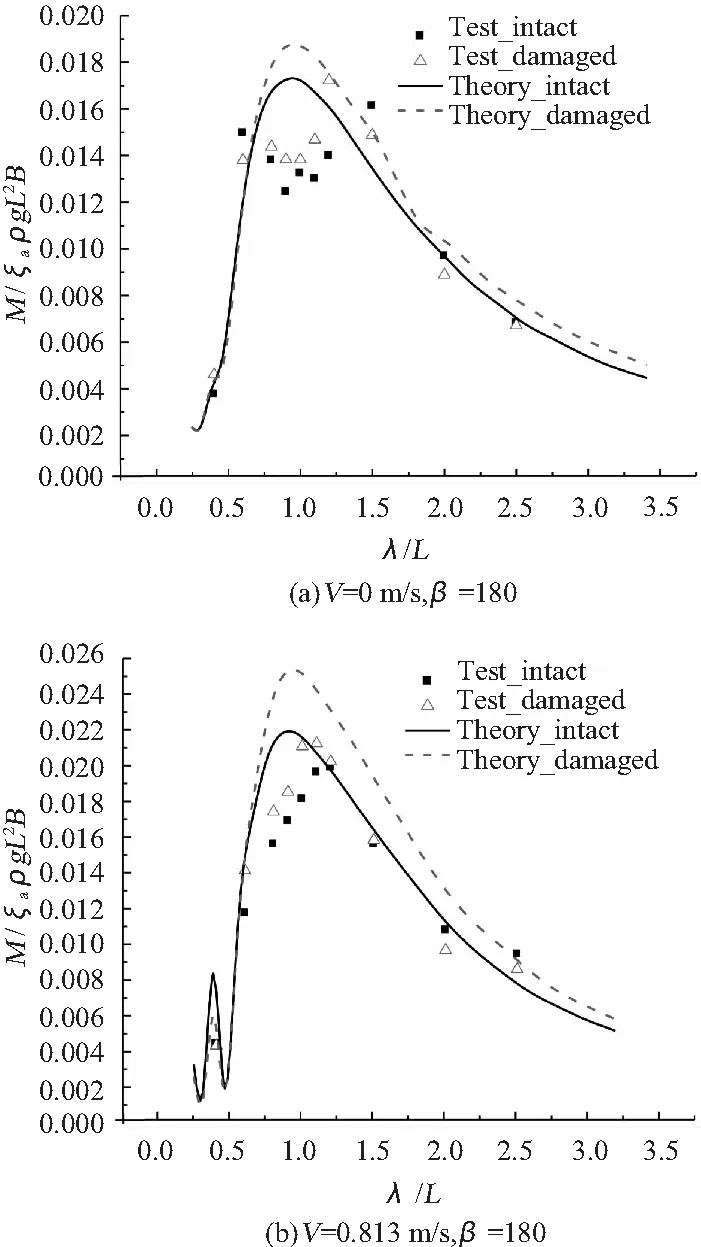
图5 船中垂向波浪弯矩RAO比较Fig.5 Comparison of V.B.M′s RAO in mid-ship

由图3～图5可看出:

1)试验结果与理论预报结果均显示：当船体发生破损后，船体纵摇响应减小，在V=0.813 m/s时更为明显；船体垂荡运动基本不变。

2)与完整正浮时相比，破损后的船体垂向波浪弯矩在峰值附近有较明显的增大，试验结果在V=0.813 m/s时峰值增加8.32%。

3)理论预报能够正确反映出船体破损后在波浪中的响应变化，且与试验结果符合较好，但理论预报的纵摇响应与波浪弯矩峰值比试验值偏大。

4 结 语

为了研究舰船破损前后在波浪中响应的变化，本文开展了船模水池试验并做了理论预报。通过对比分析，理论预报结果与试验结果符合较好，验证了理论计算方法。理论预报与试验结果均显示：该舰船发生破损后，纵摇响应减小，垂荡响应基本不变，垂向波浪弯矩在峰值附近有较明显的增大。垂向波浪弯矩的增加对破损后的舰船结构十分不利，有可能会使得舰船出现进一步的破损。通过开展对舰船破损前后在波浪中响应的变化的研究，可为对舰船破损后生命力的研究提供依据。

[1] KORKUT E,ATLAR M,INCECIK A.An experimental study of global loads acting on an intact and damaged Ro-Ro ship model[J].Ocean Engineering,2005,32:1370-1403.

[2] KORKUT E,ATLAR M,INCECIK A.An experimental study of motion behavior with an intact and damaged Ro-Ro ship model[J].Ocean Engineering, 2004,31:483-512.

[3] CHAN HS,ATLAR M,INCECIK A.Large-amplitude motion responses of a Ro-Ro ship to regular oblique waves in intact and damaged conditions[J].Marine Science and Technology,2002,7:91-99.

[4] CHAN HS,ATLAR M,INCECIK A.Global wave loads on intact and damaged Ro-Ro ships in regular oblique waves[J].Marine Structures,2003,16:323-344.

[5] LEE YW,CHAN HS,PU YC,et al.Global wave loads on a damaged ship[R].Lloyd′s Register,2012.

[6] 吴明远.破损船舶运动与波浪载荷的三维计算方法研究[D].哈尔滨：哈尔滨工程大学,2007.

WU Ming-yuan.Study of 3D calculation method of damaged ships' motion and wave load[D].Harbin:Harbin Engineering University.2007.

[7] 青兆熹.破损船舶波浪运动载荷计算方法研究[D].哈尔滨：哈尔滨工程大学,2009.

QING Zhao-xi.Study of calculation method of damaged ships′ motion and wave load[D].Harbin: Harbin Engineering University.2007.

[8] 戴仰山,沈进威.船舶波浪载荷[M].北京：国防工业出版社,2007.

DAI Yang-shan,SHEN Jin-wei.Ship wave loads[M].Beijing:National Defense Industry Press,2007.

[9] 孙伯起.低航速物体在波浪上的运动理论和波浪阻尼计算[R].无锡：CSSRC研究报告,1990.

SUN Bo-qi.Ship′s motion theory and wave resistance calculation with low speed[R].Wuxi:CSSRC Research Report,1990.

[10] 邹元杰,段文洋,任慧龙，等.船舶在波浪中脉动压力预报的三维方法[J].哈尔滨工程大学学报,2002,23(1):20-25.

ZOU Yuan-jie, DUAN Wen-yang,REN Hui-long,et al.Three-dimensional method for prediction of oscillation pressure on ship waves[J].Journal of Harbin Engineering University,2002,23(1):20-25.

Prediction and model test of responses of damaged vessels in waves

FENG Qian-dong,HU Jia-jun,ZHANG Fan,GENG Yan-chao

(China Ship Scientific Research Center,Wuxi 214082,China)

Aimed at studying the responses of damaged vessels in waves, intact and damaged vessel models′ tests were carried out. Numerical predictions to the responses of intact and damaged vessels in waves were made by using 3D linear potential theory in frequency domain. Numerical predictions match the results of models tests well, verifying the prediction theory. Finally, the influence of damage to the vessel′s responses in waves was analyzed by comparing the responses with the intact vessel′s.

damaged vessels;model test;three-dimensional method in frequency domain

2013-12-27;

2014-02-19

冯乾栋(1989-)，男，硕士研究生，研究方向为船舶与海洋工程环境载荷。

U661.32

A

1672-7649(2014)11-0029-04

10.3404/j.issn.1672-7649.2014.11.006