界面脱胶圆衬砌对出平面动力的响应

南景富

(黑龙江科技大学 理学院，哈尔滨150022)

由于自然因素或人为需要等原因，用于工程实际的天然材料或人工合成材料，一般具有界面、衬砌、脱胶、裂纹等结构，如为加固地铁隧道、煤矿巷道、涵洞等而建造的衬砌，因对跨越断层和全断面开挖施工带来的地下土质岩石等性质变化而形成的界面，在地震、爆炸等冲击载荷或温度变化时衬砌和其他材料间出现的脱胶缺陷等。研究衬砌结构对反平面动力的响应与动应力集中情况，不但可以在理论上为研究界面结构的动力响应问题提供新模型，还可为诸如地铁隧道、煤矿巷道、涵洞等的设计施工等工程实际问题研究提供参考，因此，具有十分重要的意义［1－4］。

笔者采用数学物理方法中的Green 函数法研究全空间中含有界面和半圆形脱胶的圆形衬砌复合结构对任意角度入射出平面动力波的响应问题，即在出平面动力波作用时产生的位移场和应力场，并以此为基础，推导并讨论衬砌周边动应力集中因数的函数方程。

1 问题的Green 函数解

含有界面和半圆形脱胶衬砌的全空间力学模型如图1 所示。

图1b 所示上半空间的Green 函数为

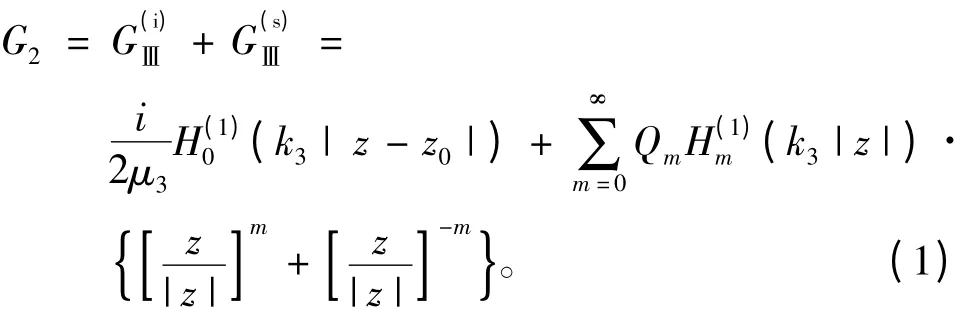
图1c 所示下半空间的衬砌内Green 函数及下半空间其余部分Green 函数为可分别表示为

式(1)～(3)中待求常数的物理意义参见文献［5 －11］。

2 问题的求解

2．1 出平面波力学模型

图1 也显示了出平面波以任意角度α0入射时产生的入射波、反射波和折射波力学模型。

图1 力学模型及SH 波入射模型Fig．1 Mechanics model and model of incidence of SH-wave

在下半空间的界面上位移函数和应力函数［11］计算式为

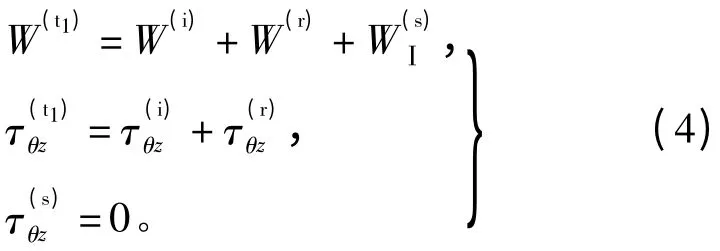
在上半空间的界面上位移函数和应力函数［11］计算式为

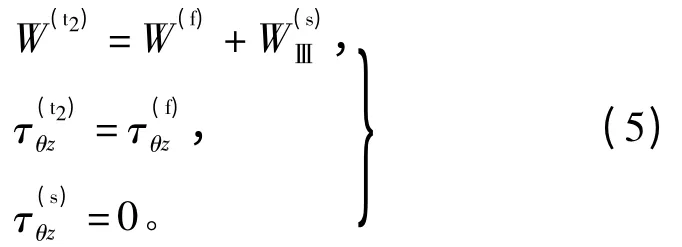
2.2 模型契合

将含界面和半圆形脱胶衬砌的上半空间和下半空间两部分契合在一起，其力学模型如图2 所示。

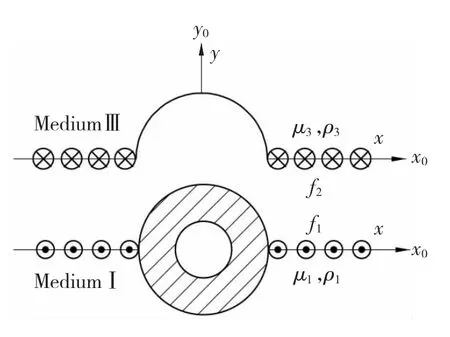
图2 模型契合示意Fig．2 Forming bi-media material

求解f1(r0，θ0)的积分方程组［5－11］为

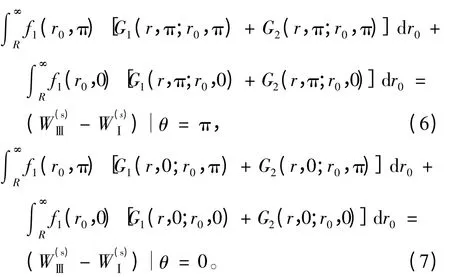
2.3 应力求解

通常，弹性衬砌周边的动应力集中因数(DSCF)表达式为

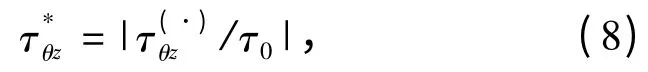
式中:τ(·)θz——弹性衬砌周边上的应力;

τ0——入射应力的最大幅值，τ0=μ1k1W0。

在下半空间，弹性衬砌附近周边的应力可通过下面公式计算:

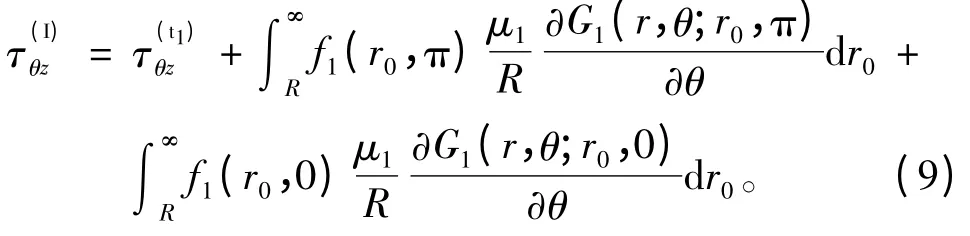
在上半空间，半圆形凹陷周边的应力可以通过下面公式计算:

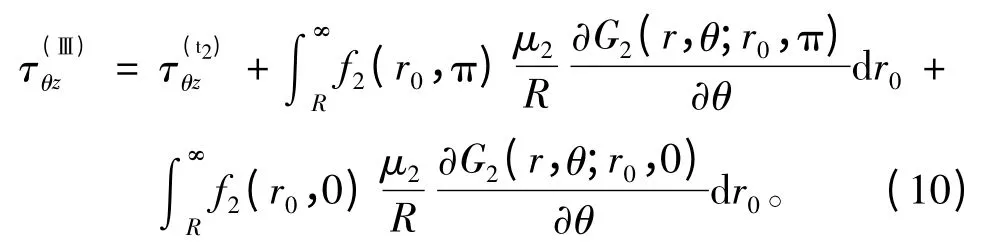
3 数值计算与分析

数值计算相关参数为:k =ω/cs，ω 为位移函数的圆频率;cs为材料的出平面波波速ρ、μ 分别为材料的密度和剪切模量;k1a 为入射波波数皆为无量纲参数。

图3 为反平面波α0=90°，材料参数组合=1.50、=0.38 的情况下，沿衬砌周边的DSCF 数值计算结果。图3a 为k1a = 0.1 时衬砌周边的DSCF 数值计算结果，由图可见，衬砌上半周边DSCF 明显大于下半区周边的DSCF。图3b 和3c 分别为k1a=1.0 和k1a =2.0 时衬砌周边的DSCF 数值计算结果，由图可见，当入射波以中、高频率入射时，下半区衬砌周边的DSCF 明显高于上半区衬砌周边的DSCF。

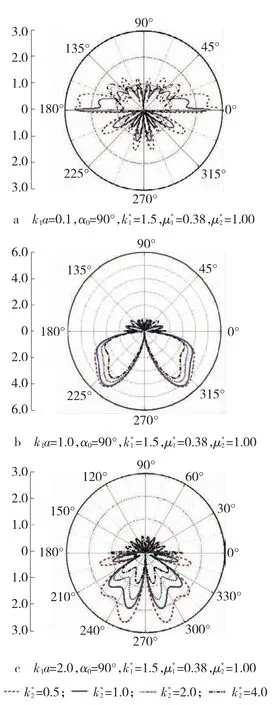
图3 反平面波α0 =90°、=0.38 时衬砌周边DSCF 的数值分布Fig．3 Distribution of DSCF around edge by anti-plane wave while α0 =90° and=0.38

图4 为反平面波α0=90°，材料参数组合=0.70、=3.23 的情况下，沿衬砌周边的DSCF 数值计算结果。由图可见，图4a 与图3a 同为k1a =0.1 时，衬砌周边DSCF 分布情况总体趋势相同。图4b 和4c 分别为k1a =1.0 和k1a =2.0 时衬砌周边的DSCF 数值计算结果。由图可见，当入射波以中、高频率入射时，虽然下半区衬砌周边的DSCF 也高于上半区衬砌周边的DSCF，但并没有图3b 和图3c 明显。由此反应出变化对DSCF的分布有影响。

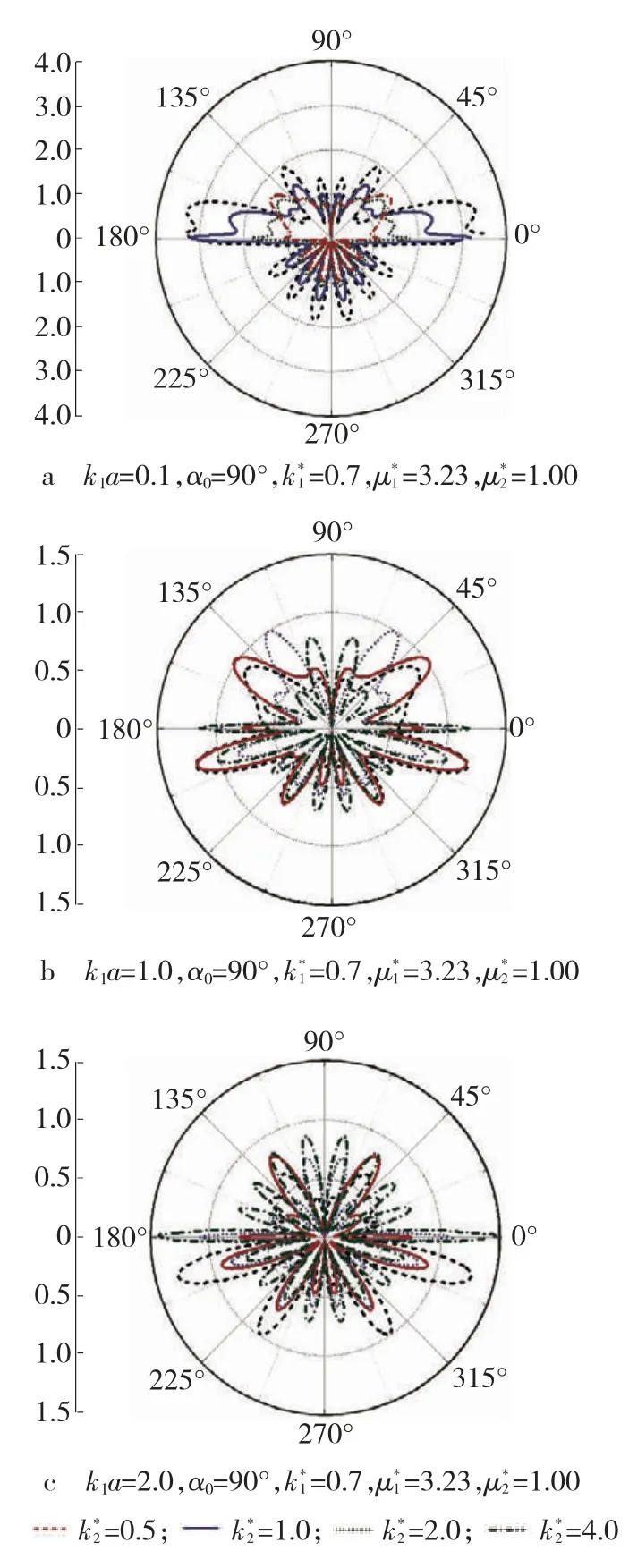
图4 反平面波α0 =90°、=3.23 时衬砌周边DSCF 的数值分布Fig．4 Distribution of DSCF around edge by anti-plane wave while α0 =90° and =3.23

由图3 和图4 可见，当k1a =0.1 时，DSCF 的最大值出现在分界面处，当k1a =2.0 时，分界面处的DSCF 明显减小。

由图5 和图6 可见，k1a =0.1、α0=90°时衬砌周边DSCF 最大值明显小于k1a =0.1、α0=45°时的最大值;k1a=2.0、α0=90°时DSCF 最大值明显小于k1a =2.0、α0=45°时的最大值;α0=45°时DSCF 分布变化复杂，最大值仍多数会出现在分界面附近。

通过算例分析可以看出，入射波数、入射角度以及介质参数等因素均对全空间中双相介质界面附近半圆形脱胶的圆柱形衬砌的周边动应力集中因数有一定的影响，尤其对界面点处动应力集中因数的放大作用。由于界面是结构或者材料强度的薄弱区域，所以要非常注意界面点的动应力集中因数随入射波数的变化曲线。文中仅对μ*、k*两个介质参数进行了讨论，这是由于μ、ρ、k 中只有两个是独立的。

图5 反平面波α0 =45°、=0.38 时衬砌周边DSCF 的数值分布Fig．5 Distribution of DSCF around edge by anti-plane wave while α0 =45° and =0.38

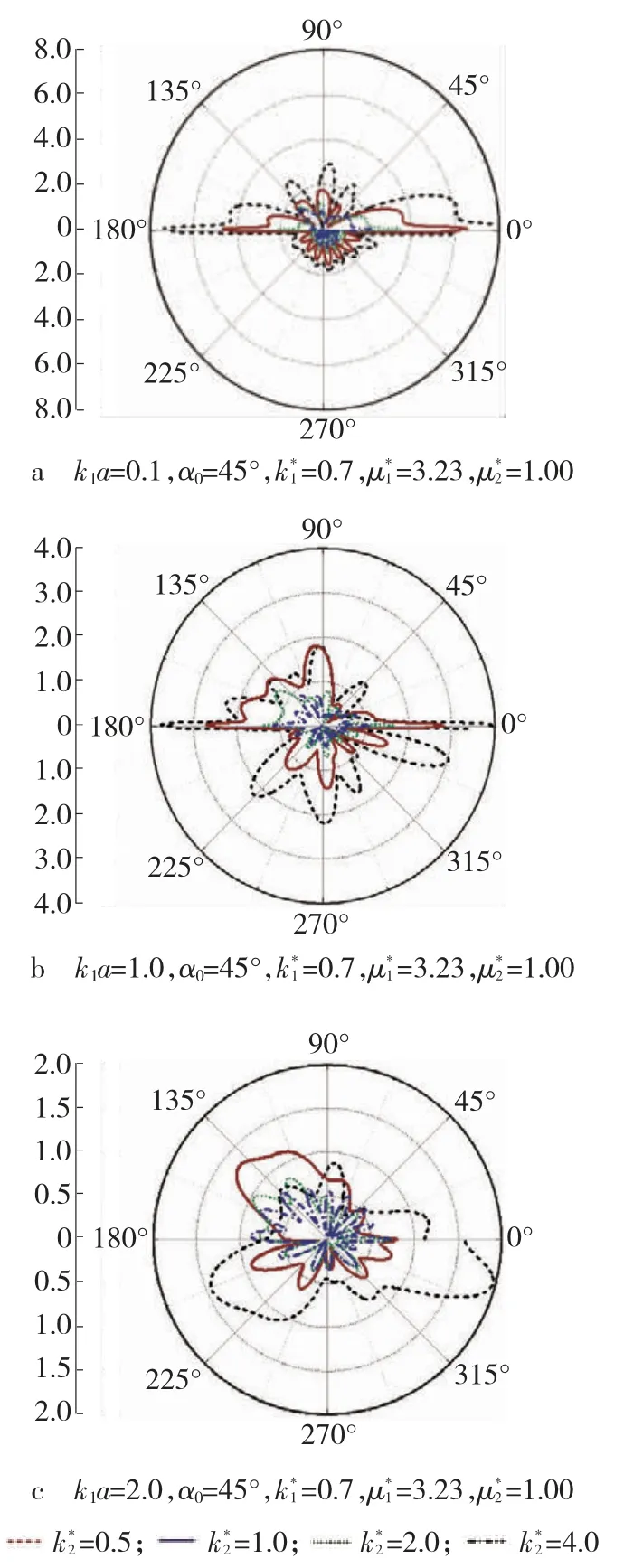
图6 反平面波α0 =45°、=3.23 时衬砌周边DSCF 分布Fig．6 Distribution of DSCF around edge by anti-plane wave while α0 =45° and=3.23

4 结 论

采用Green 函数法研究含有界面和半圆形脱胶衬砌对出平面动力的响应问题。由数值算例结果可知，k1a、α0以及μ*等的变化对该模型衬砌的周边动应力集中因数(DSCF)有一定的影响，尤以对界面点处的DSCF 作用明显。

［1］鲍亦兴，毛昭宙．弹性波的衍射与动应力集中［M］．北京:科学出版社，1993．

［2］陈志刚，刘殿魁．椭圆孔对SH 波散射的远场解［J］．哈尔滨工程大学学报，2003，24(3):334 －338．

［3］杨在林．界面可移动圆形刚性夹杂对反平面波散射和它的远场解［D］．哈尔滨:哈尔滨工程大学，2000．

［4］齐 辉．界面圆环形衬砌对反平面波散射及动应力集中［D］．哈尔滨:哈尔滨工程大学，2000．

［5］NAN JINGFU，QI HUI，SHI YONG．Scattering of SH-waves by cylindrical lining debonded near bi-material interfaces［J］．Advanced Science Letters，2011(3):1281 －1285．

［6］南景富，齐 辉，折 勇．垂直半空间裂纹及附近圆孔对SH波的散射［J］．工程力学，2009(5):245 －250．

［7］QI HUI，SHI YONG，NAN JINGFU．Ground motion of non-circular alluvial valley for incident plane SH-wave［C］//The 14thWorld Conference on Earthquake Engineering．Beijing:［s．n．］，2008．

［8］南景富，齐 辉，韩 刘，等．SH 波作用下地表覆盖层与浅埋圆柱形夹杂的相互作用［J］．自然灾害学报，2010(2):169 －174．

［9］NAN JINGFU，QI HUI，ZHAO CHUNXIANG．Scattering of SHwaves by interface semicircular debonded cylindrical lining and linear cracks originating at edge of lining［J］．Advanced Materials Research，2011，399 －401:2149 －2154．

［10］南景富，齐 辉．含半圆形衬砌凸起弹性半空间问题的Green 函数解［J］．工程力学，2012(5):31 －36．

［11］南景富．界面圆形脱胶衬砌与裂纹对反平面波的散射［D］．哈尔滨:哈尔滨工程大学，2012．