基于多点位移控制的梁柱节点刚度对钢框架抗震性能的影响①

洪 敏，冯红卫，王 凤，赵林林，高永国

（1.中国地震局兰州地震研究所，甘肃 兰州 730000；2.中国科学院寒区旱区环境与工程研究所，甘肃 兰州 730000；3.中国科学院大学，甘肃 兰州 730000；4.甘肃省高性能网格计算中心，甘肃 兰州 730000；5.新乡学院土木工程与建筑系，河南 新乡 453003；6.西安建筑科技大学土木工程学院，陕西 西安 710055）

0 引言

传统的框架计算分析时通常将框架节点考虑成刚度无穷大的刚性节点和刚度为零的铰接节点。许多实验结果证实［1］，实际工程中采用的节点形式其弯矩和相对转角的关系既非完全刚接，也非理想铰接，而是呈非线性连接状态，称为半刚接。多次地震表明［2］，半刚性钢框架因节点具有较强的耗能能力可以抵挡一定的地震荷载，同时可以减少斜撑的数量及节点用钢量，使得半刚接钢框架成为一种经济、可靠的选择。节点刚度体现了受外力作用的材料、构件或结构抵抗变形的能力，是衡量节点连接性能的主要因素之一，不同的节点刚度对钢框架的抗震性能有显著影响。但目前有关节点刚度对钢框架抗震性能的影响的研究相对较少。Elnashai［3］进行了8个两层刚接及半刚接钢框架单向、循环加载及伪动力实验研究，发现节点刚度对框架结构的刚度和承载力有较大影响；郭兵［4］进行了6榀刚接及半刚接钢框架的循环加载实验研究和动力性能测试，发现节点刚度较低时框架的承载能力和耗能能力较低，不利于结构抗震；郭兵和雷淑忠［5］指出随着节点转动刚度的逐渐降低，框架侧向刚度减小，侧移增大，框架柱脚很容易率先屈服，梁端很难形成塑性铰，导致结构耗能能力降低。但是上述研究都只是定性地给出了结构的抗震性能随节点刚度的变化规律，没有定量地给出框架节点设计时连接刚度的合理界限。

针对上述不足，本文采用ABAQUS软件，对一组典型六层两跨钢框架模型在多点位移控制下的抗震性能进行分析，通过定义模型节点连接为不同的刚度值，对比分析结果，以给出节点刚度影响系数α的最佳范围。

1 节点刚度判定准则

梁柱连接在外力作用下变形的同时传递轴力、剪力、弯矩和扭矩。对于大多数连接，轴向、剪切以及扭转引起的变形与弯曲变形相比都很小，可以忽略不计，因此连接的特性通常用弯矩—转角曲线来描述［6］。本文采用文献［7］中的节点计算模型（图1），取Kf＝1／40 K0，通过给定不同K0值，从而计算得到不同的节点刚度影响系数α；将梁柱节点定义为不同的连接形式，分析不同连接刚度对框架抗震性能的影响。

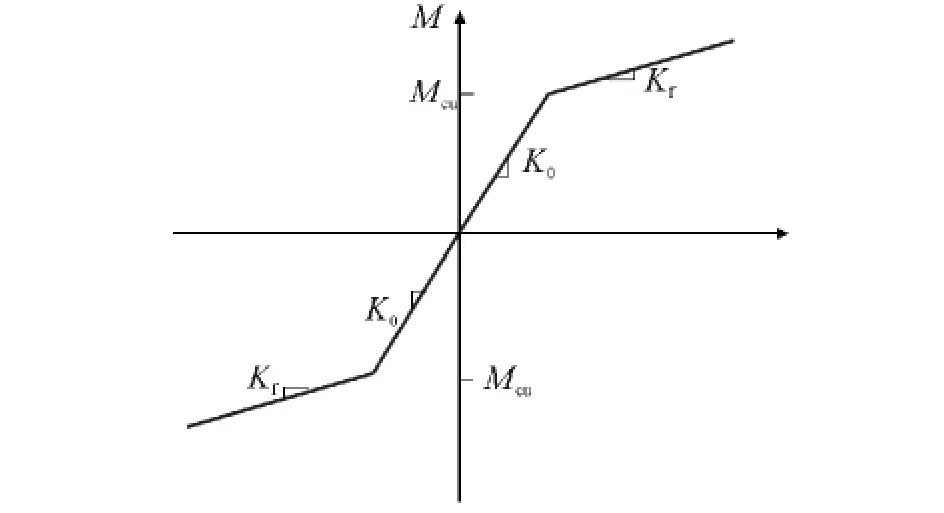
图1 节点的M－θ关系曲线Fig.1 The M－θcurves of the node

2 有限元模型的建立及验证

2.1 有限元模型的建立

本文采用ABAQUS软件中二维梁单元（B21）建模，通过在梁上附加线荷载定义楼板，采用SPRING2来模拟梁柱节点连接，参照文献［8］进行设置。

钢材的应变关系采用三折线模型，参照文献［9］进行取值。采用Mises屈服准则，本构关系为考虑包辛格效应的运动强化模型。本文建立的平面模型不需考虑平面外自由度，只需约束柱脚底部全部自由度。通过先对框架进行单向加载，根据得到的荷载—位移曲线确定试件屈服时的总水平荷载Py和框架的屈服位移Δy。循环加载按照Δy／4、Δy／2、3Δy／4、Δy、2Δy、3Δy、…… 的方式进行，模型屈服之前的各级位移循环一次，屈服后的各级位移循环两次，当框架中某层层间侧移角达到5%时认为结构试件破坏。

有限元模拟多质点比例加载，采用位移控制时需要在原有结构上增加位移约束方程［10］，保证推覆分析中保持恒定侧力分布。在ABAQUS中定义位移约束方程实现多质点的位移加载时，定义结构模型外的参考点Z，通过定义Z点在m方向上的位移变化，成比例的约束定义的节点在m方向上的位移加载控制，实现位移的耦联：

其中，ui为第i个节点在水平方向上的位移；Ai表示Z点在荷载的比例系数，是一个任意不为0的数；uz为引入的“孤立”点Z在水平方向上的位移，即输入的外控制位移。本文采用倒三角比例加载，荷载比例为1∶2∶3……（一层：二层：三层）。

2.2 模型验证

为了验证本文所述的建模方式的合理性，对文献［4］中S2系列试件进行模拟，并与试验结果进行对比。有限元模型采用试验实际材性，并根据试验相同几何尺寸建立平面框架模型。图2为有限元模拟及试验的骨架曲线及滞回曲线对比图。表1给出了有限元计算和试验的对比结果。其中，μ为延性系数（μ＝Δu／Δy）；Ce为能量耗散系数（参照文献［11］计算）；K 为侧向刚度（K＝Py／Δy）。由对比结果可见，有限元模拟的骨架曲线略高于试验曲线，能耗系数稍偏大。原因在于有限元模型未考虑初始几何缺陷及焊接残余应力的影响，且有限元模型为平面模型，未考虑平面外的荷载及位移。但有限元模型侧向刚度与实验值相当接近，骨架曲线、滞回曲线误差较小，可见有限元模拟与试验结果总体吻合较好，因此上述建模方法可用来进行后续的模型分析。

表1 有限元计算结果和试验结果的比较Table 1 Comparison of results from experiment［4］and finite element analysis

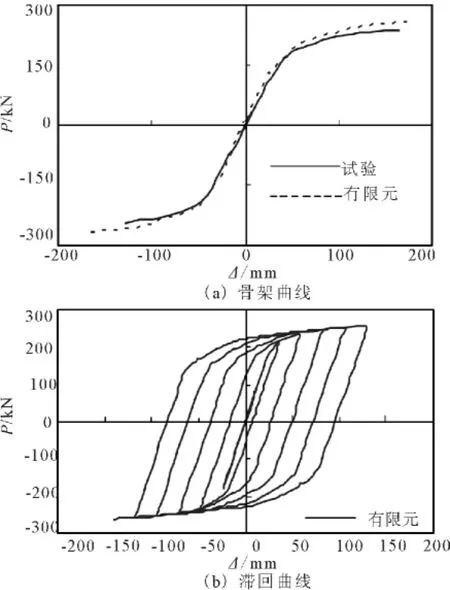
图2 有限元模拟与试验结果［4］的骨架曲线和滞回曲线对比Fig.2 Comparison of the skeleton curves and hysteresis curves between the finite element analysis and test result from reference［4］

3 试件抗震性能分析

3.1 试件设计

为了探讨节点连接刚度对框架抗震性能的影响，设计了某典型六层两跨平面钢框架进行分析。跨度为7.2m，层高为3.6m，采用平面框架将楼板作用等效为框架上施加竖向均布荷载q＝25kN／m，水平荷载可按倒三角形分布，宜通过各层楼板施加。试件梁柱截面均为焊接H型钢，材质为Q235钢，其中梁截面为H450mm×200mm×8mm×12 mm，柱截面为 H350mm×350mm×11mm×16 mm。

引入节点刚度影响系数α为梁线刚度与节点初始刚度K0之比的平均值［12］。本文设置一系列试件H1～H9，根据文献［13］中节点半刚接的定义，设定节点刚度影响系数α分别为4（铰接）、2（铰接）、1（半刚接）、1／5（半刚接）、1／10（半刚接）、1／15（半刚接）、1／20（半刚接）、1／25（刚接）、1／50（刚接），构成9条具有代表性的M－θ曲线，赋予各模型节点连接刚度。通过对具有不同节点影响系数的钢框架进行单项加载及循环加载，分析α变化时对其抗震性能的影响。

3.2 单向加载计算结果

试件H1～H9单向加载的曲线见图3所示，Py为水平总荷载，Δ为框架顶点水平侧移，表2给出了单向加载的计算结果。

表2 单向加载计算结果Table 2 The result of monotonic loading

由图3可以看出随着节点刚度影响系数α的减小和节点连接刚度的增加，各试件的屈服荷载、极限荷载及侧向刚度都有所提高。但是随着节点刚度越接近刚性连接，增加趋势越来越小。实际工程中的梁柱连接节点大都是半刚性的，由表2数据可知，本文分析的模型中当梁柱节点为半钢接且α介于1／15～1／20时，框架的屈服荷载和极限荷载均能达到节点刚接时的94%以上，侧向刚度均能达到节点刚接时的70%以上，能够满足承载力的需求。

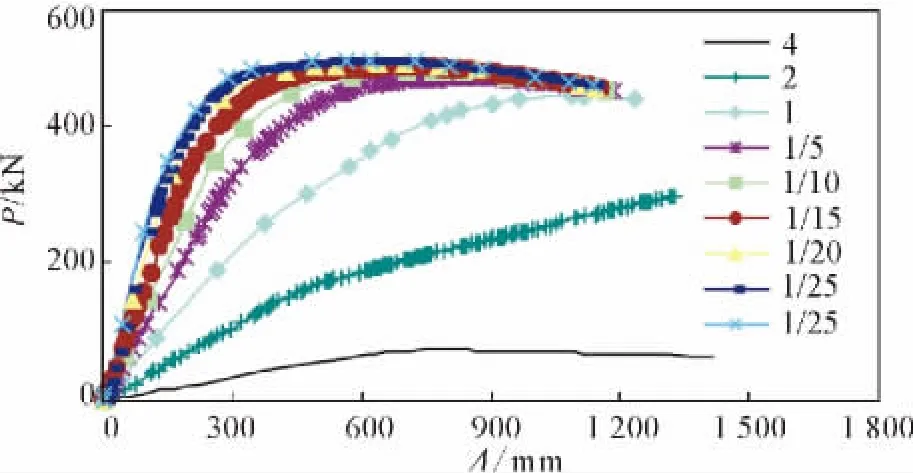
图3 试件单向加载P－Δ曲线Fig.3 The P－Δcurves of test samples under monotonic loading

3.3 循环加载计算结果

多点位移控制的循环加载可以模拟地震荷载的往复振动作用，同时又考虑了构件双向受力的影响，从而更合理地模拟了地震作用的往复特征［14］。图4为各试件在循环荷载作用下的滞回曲线。由图中可以看出，除H1、H2外的其余试件滞回曲线饱满、稳定、呈梭形、无捏拢现象，表现出了良好的耗能能力。

从图中不难看出，随着α的变化，各个试件的抗震性能存在较大差异，体现了节点刚度对结构抗震性能的影响。以下讨论α对框架延性、耗能能力及刚度退化的影响。表3给出了模型的顶层侧移、总侧移角及延性系数，其中H为结构总高度。

（1）延性及耗能能力

延性是指结构或构件屈服后的后期变形能力；耗能能力是指构件在反复荷载作用下结构发生塑性变形以及吸收和消耗能量的能力。工程上常用等效粘滞阻尼系数εe表示结构的耗能能力。参照文献［11］进行计算。

从表3可以看出各个模型随着α的减小，延性系数、等效粘滞阻尼系数逐渐增大，结构的抗震性能逐渐增强。当梁柱节点为半钢接且α介于1／10～1／20时，框架的屈服荷载和极限荷载均能达到节点刚接时的98%以上，框架的延性系数μ为节点刚接时的70%以上，等效粘滞阻尼系数εe为节点刚接时的67%以上。当α介于1／15～1／20时，框架的延性系数μ及等效粘滞阻尼系数εe均能达到节点刚接时的80%以上，抗震性能良好。

（2）刚度退化

为了反映各模型刚度退化规律，本文采用割线刚度Ki，由文献［11］中的方法计算得到。图5给出了各个模型的刚度退化曲线。从图中可以很直观地看到，当α介于1／50～1时，随着节点α减小，各模型初始刚度损伤更严重，其继续承担荷载的能力减弱。综合考虑，当α介于1／15～1／20时，模型初始刚度较高，且刚度下降幅度不大，约在74.6%～79.1%，具有一定继续承担荷载的能力。

表3 模型的延性系数及等效粘滞阻尼系数Table 3 The ductility factors and equivalent viscous damping coefficients of model

图4 循环荷载下的试件荷载—位移曲线Fig.4 The hysteresis curves of test samples under cyclic loading

图5 刚度退化曲线Fig.5 The stiffness degradation curves

4 结论

本文通过对一组梁柱节点刚度不同的框架模型进行单向加载及循环加载分析，可初步得到以下结论：

（1）通过定义梁柱节点连接的初始转动刚度及节点连接的M－θ曲线可以模拟不同刚度的梁柱节点连接。在ABAQUS有限元分析中，通过定义结构模型外一参考点Z及某方向上的位移约束方程，可实现该方向上的多点位移控制加载。

（2）本文的模型中分别定义了铰接、半刚接、刚接三种不同的梁柱节点连接形式，对比分析了随着节点刚度影响系数α变化时模型抗震性能的差异。随着α的减小，模型的承载力、侧向刚度、延性及耗能能力都逐渐增加，但增加趋势减小；而模型的初始刚度损伤逐渐加重，其继续承担荷载的能力减弱。

（3）由于实际工程中几乎不存在理想的铰接及刚接情况，且不同梁柱连接刚度对结构抗震性能影响较大，设计时必须考虑。综合本文模型的分析结果，当α介于1／15～1／20时，不仅能满足承载力的需求，而且框架的延性、耗能特性良好，初始刚度较高，下降幅度不大，具有较好的抗震性能。

（References）

［1］Chen W F.Steel Beam－Column Building Connections［M］.New York：Elsevier Science Publishing Co I NC，1988：1－33.

［2］Astaneh－Asl A.Seismic Performance and Design of Bolted Steel Moment－resisting Frames［J］.Engineering Journal，A－merican Lnstitute of Steel Construction，1999，36（3）：105－120.

［3］Elnashai A S，Eldhazouli A Y，Denesh－Ashtiani F A.Response of Semi－rigid Steel Frames to Cyclic and Earthquake Loads［J］.Journal of Structural Engineering ASCE，1998，124（8）：857－867.

［4］郭兵，郭彦林，柳锋，等.焊接及螺栓连接钢框架的循环加载实验研究［J］.建筑结构学报，2006，27（2）：47－56.GUO Bing，GUO Yan－lin，Liu Feng，et al.Research on Cyclic Behavior of Welded and Bolted Steel Frames［J］.Journal of Building Structures，27（2）：47－56.（in Chinese）

［5］郭兵，雷淑忠.梁柱节点刚度对无支撑钢框架性能的影响［J］.山东建筑大学学报，2010，25（3）：231－235.GUO Bing，LEI Shu－zhong.Effects of Connection Stiffness on the Behavior of Unbraced Steel frames［J］.Journal of Shandong Jianzhu University，2010，25（3）：231－235.（in Chinese）

［6］刘永华，张耀春.半刚性钢框架实用非线性分析［J］.工程力学，2007，24（12）：6－13.LIU Y H，ZHANG Yan－chun.Practical Nonlinear Analysis for Semi－rigid Steel Frames［J］.Engineering Mechanics，2007，24（12）：6－13.（in Chinese）

［7］丁洁民，沈祖炎.一种半刚性节点的实用计算模型［J］.工业建筑，1992，（11）：29－32.DING J M，SHEN Zu－Yan.A practical Calculation Model of Semi－rigid Connection［J］.Industrial Construction，1992，（11）：29－32.（in Chinese）

［8］夏磊，张鹏鹏，王文达.半刚性连接钢管混凝土框架动力特性的非线性有限元分析［J］.工程抗震与加固改造，2013，35（1）：16－22.XIA Lei，ZHANG Peng－peng，WANG Wen－da.Nonlinear Finite Element Analysis of Dynamic Characteristics of Semi－rigid Frames with Concrete－filled Steel Tubular Columns［J］.Earthquake Resistant Engineering and Retrofitting，2013，35（1）：16－22.（in Chinese）

［9］郭兵.钢框架梁柱端板连接在循环荷载作用下的破坏机理及抗震设计对策［D］.西安：西安建筑科技大学，2002.GUO Bing.Collapse Mechanism and Design Criterion of Steel Beam－to－column end－plate Connections Under Cyclic Load［D］.Xi’an：Xi’an University of Architecture and Technology，2002.（in Chinese）

［10］黄羽立，陆新征，叶列平，等.基于多点位移控制的推覆分析算法［J］.工程力学，2011，28（2）：18－23.HUANG Yu－li，LU Xin－zheng，YE Lie－ping，et al.A Pushover Analysis Algorithm Based on Multiple Point Constraints［J］.Engineering Mechanics，2011，28（2）：18－23.（in Chinese）

［11］丁洁民，沈祖炎.节点半刚性对钢框架结构内力和位移的影响［J］.建筑结构，1991，（6）：8－12.DING Jie－min，SHEN Zu－yan.The Influence of Semi－rigid Connection to the Structure Internal force and Displacement of Steel frame［J］.Building Structure，1991，（6）：8－12.（in Chinese）

［12］British Standards Institution（Eurocode4（2004））.Design of Steel and Concrete Structures，partl.1，General Rules and Rules doe Building.BS EN1994－1－1：2004［S］.London：British Standards Institution，2004.

［13］周露，黄襄云，沈朝勇，等.多层框架连廊结构柔性连接设计及计算分析用［J］.华南地震，2013，3（1）：33－42.ZHOU Lu，HUANG Xiang－yun，SHEN Chao－yong，et al.Flexible Connection Design and Analysis in Multi－layer Framework Building with Corridor Structure［J］.South China Journal of Seismology，2013，33（1）：21－28.（in Chinese）