时频分析方法在形变数据中的应用研究①

王 宁，吴 云，张 燕

（1.中国地震局地震研究所地震大地测量重点实验室，湖北 武汉 430071；2.中国地震局地壳应力研究所武汉科技创新基地，湖北 武汉 430071）

0 引言

傅里叶变换的提出为信号处理带来了翻天覆地的变化，其应用遍及地震信号分析［1］、地质勘探［2］、机械振动信号分析［3］等各个领域。然而，经典傅里叶变换不能同时兼备时间和频率分辨率，不适宜处理诸如非平稳的地震信号。时频分析方法将传统傅里叶变换的整体谱推广到局部谱中，对于非平稳地震信号的分析具有很好的适用性。随着Gabor变换、小波变换、Hilbert－Huang变换等时频分析方法的出现，非平稳信号的时频特性得到了很好的展示。周挚等提出了固体潮时频分析新方法，即HHT方法，同时指出了该方法的特点和局限性［4］；周挚等基于HHT提取昆明、下关重力固体潮的地震前兆信息，设计了重力固体潮地震前兆分析的特征参数，得到震前异常特征参数为HHT计算得到的实际参数和理论参数的频率比值［5］；吕品姬等研究了小波分解及短时傅里叶变换在地形变观测数据中的应用，得到了不同采样率的数据其时频图的特点及所反应的物理事件［6］。然而时频分析方法在地形变数据分析中尚处于起步阶段，还没有得到普遍应用。

本文通过小波变换、Hilbert－Huang变换及S变换在设计数据以及地形变数据分析中的应用，分析比较三种方法，以得到这些方法的特点和局限性，为以后方法的利用提供依据。

1 算法

1.1 小波变换

小波变换最早由法国的地球物理学家于上世纪80年代提出，因其兼具了时间和频率的分辨率，被称为联合时频分析，简称时频分析。信号h（t）的小波变换定义为

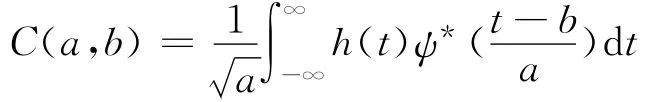
式中，a表示尺度因子；b表示平移因子；ψ（t）为基本小波或母小波。基本小波必须满足容许性条件，即

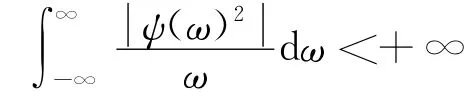
小波变换的母小波具有多种形式，本文采用的是分析非平稳信号常用的cmor3－3小波。

1.2 S变换

S变换是以Morlet小波为基本小波的连续小波变换的延伸［7］，它结合了短时傅里叶变换和小波变换的优点，解决了短时傅里叶变换窗口频率不能调节的问题，同时具备了小波变换多分辨率的优势，而且基本小波不用满足容许性条件。信号h（t）的S变换定义为［8］

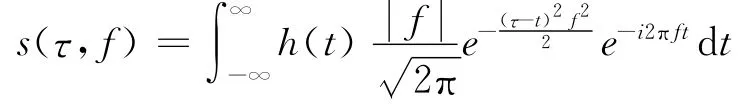
S变换不同于小波变换，采用与频率有关的可变高斯窗函数，其时频分辨率与频率有关，信号的变换结果与其傅里叶谱保持直接联系。因此通过S变换及其逆变换可以实现信号在时－频域的无损转换，这些特点使得S变换在分析非平稳信号过程中得到了广泛的应用［9］。

1.3 Hilbert－Huang变换［10］

Hilbert－Huang变换是一种基于经验的数据分析方法。其核心思想是把非线性非平稳信号看成是由若干的本征函数构成，通过经验模态分解（EMD）将其分解出来，然后利用Hilbert变换构造解析信号，得到数据的瞬时属性，进而得到其时频谱。

1.3.1 经验模态分解（EMD）

经验模态分解建立的前提是假设任何数据都是由一系列的本征模态函数（IMF）构成，IMF需满足以下两个条件：（1）整个数据中，极值点和过零点的数量应保持一致或最多相差一个；（2）在任意点处，由极大值和极小值定义的包络线的均值应该为0。

EMD方法包括以下过程：首先，找出原始数据序列x（t）的所有极大值和极小值，并用三次样条曲线拟合其上下包络线；用原始数据x（t）减去上下包络线的均值m1（t）得到第一个分量h1（t），一般情况下h1（t）不满足IMF条件，需要重复以上处理过程；经过k次处理后产生第一个IMF分量c1（t），即

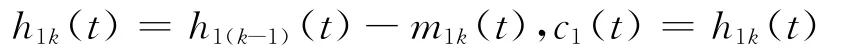
其次，将原始数据序列x（t）减去c1（t），得到余量r2（t）；重复以上步骤得到rn（t）。最后，可知原始数据可以由以上IMF分量及余量叠加而成。即

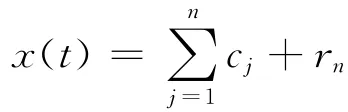
经EMD分解变换得到的IMF序列是直接从原始时序数据中分离出来的，事先无需确定分解阶次，不受人为因素影响，不存在机械分解。因此IMF序列能更好反映原始数据固有的物理特性，其分解是客观的、内在的和自适应的［11］。

1.3.2 Hilbert变换及瞬时属性提取

将每一个IMF进行Hilbert变换，进而计算出信号的瞬时频率，通过合成得到的就是HHT时频谱。

2 实验数据分析

实验将设计的仿真信号分别进行S变换、Morlet小波变换以及HHT变换，得到这三种方法的时频图，研究它们在分析数据上的适用范围。

2.1 单频率的正弦波

图1 正弦曲线的时频图Fig.1 Time－frequency spectrum of sinusoid

地形变数据具有典型的波动特性，图1给出了频率为1Hz、出现在40～50s期间的正弦波曲线。图1（d）中为显示HHT时频图的细节信息，将其40～55s处图形放大。从图可以看出，3种时频分析方法在40～50s时刻都能很好地显示正弦信号的频率信息，且都具有很好的时间和频率分辨率。其中，S变换其频率分辨率较低，图上显示为图谱较宽；小波变换低频处存在虚假频率；HHT方法低频扰动和频率分辨率都较好，但其端部效应明显。

2.2 不连续的正弦波

为验证三种时频方法对突变频率的检验，图2采用两个不同频率（f1＝1Hz，f2＝2Hz）信号合成的信号进行对比分析，比较在频率变化处三种方法的优劣。

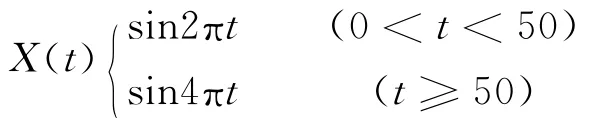
从图2可以看出，三种方法都能很好地在频率突变处对不同频率进行区分，其中小波变换和S变换得到的效果图由于存在时间和频率分辨率的问题，显然在两个不同的频率处的分辨率不同，高频部分的频率带变宽，尤其S变换高频处的频率分辨率更低，HHT则不存在分辨率不统一的问题。但三种方法在频率的突变处都存在交叉影响，端部效应也比较明显。

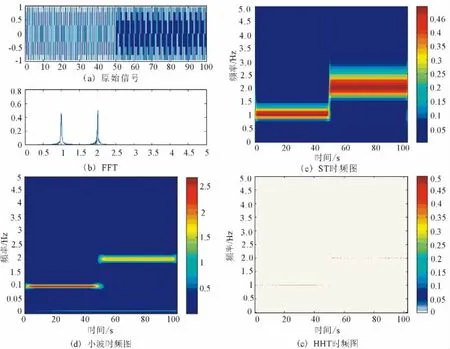
图2 3种方法对突变频率的检验Fig.2 Three methods for the inspection of mutation frequency

2.3 多频率成分数据

地形变数据同一时间往往具有多个频率成分。为验证这一特点，图3采用频率随时间变化较大的信号，也是经典的S变换采用的实例信号进行比较。

其中len为一常量，表示采样的数据点数。

从对具有多频段的模拟信号的分析来看，S变换和小波变换可以显示出信号在某段时间内的频率及其能量的变化趋势，而HHT由于每一个时刻由不同的点表示不同的频率，因而更适合分析信号的瞬时特性。S变换在低频部分的分辨率明显优于小波变换的分辨率，小波变换容易产生低频的虚假信号。

总体来看，在做连续时间序列的时频分析中，HHT方法不适合做相关分析。小波变换与S变换均可作为时频分析的有效工具，应根据所分析对象包含的频率信息选择适当方法，低频信息较多地采用S变换，高频信息较多且频率成分较多地采用小波分析方法；在分析高低频率混杂的数据时，可先做 小波分析，进一步针对某一低频事件做S分析。

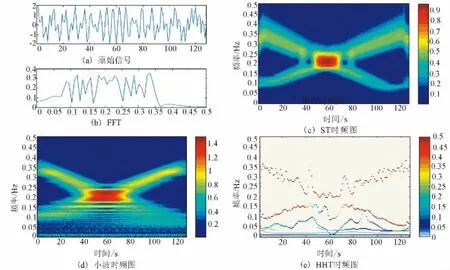
图3 多频率成分的时频分析比较Fig.3 Comparison of multiple frequency data＇s time－frequency analysis

3 地形变观测数据时频分析

在对上述三种时频分析方法各自的优越性及适用范围进行对比分析的基础上，本文采用部分地形变数据作进一步的分析。

3.1 宽频带数据应用

研究资料为汶川地震前前1小时距离较近的郫县台和安康台的宽频带数据（数据采样频率为2 Hz）。汶川地震震中经度为103.4°，纬度为31°。选择的两个台站的位置和汶川地震的震中距如表1。

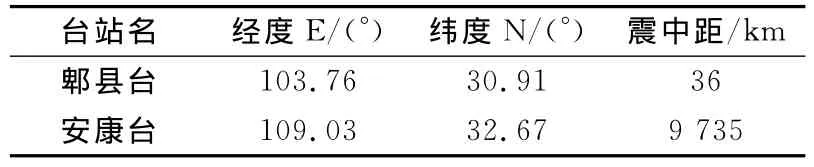
表1 台站的震中距Table 1 Position of the stations

对两个台站的宽频带数据分别使用三种时频分析方法进行处理，结果见图4、5。看出在分析宽频带数据时，HHT不能揭示信号随时间的频率变化趋势，S变换和小波变换显示了地震信号存在0.1～0.3Hz的频率信息。还可以看出，S变换较小波变换在高频部分具有很好的时间分辨率，低频部分具有很好的频率分辨率，且产生的虚假频率较少，但其高频部分的频率分辨率略低于小波变换。

秒采样数据量较大，在做时频分析时得到的是震前一小时的图谱，可以看出通过秒采样得到的图谱震前异常不明显，与台站距离地震的远近关系不大。震前异常尚有待进一步的研究。

3.2 洞体应变数据的应用

选取了2008年3月到6月黄梅洞体应变NS分量的数据及黄梅台水管倾斜NS分量的数据，采样周期为小时。三种时频分析方法的结果见图6、7。可以看出，S变换和小波变换时频图上的固体潮日波，半日波较明显，且与傅里叶谱的频率值对应；HHT谱不能用在揭示这种长周期性连续性事件上；S变换在低频部分的分辨率显然高于小波变换，产生的虚假频率较少。从小波和S变换图中可以看到5月12日前产生了一段低于日波频率的信号，且信号强度在临震时逐渐加强，这是否与2012年5月12日汶川地震有关，有待进一步的证实。

4 结果与讨论

（1）从仿真信号的时频图分析，小波变换、S变换以及Hilbert－Huang变换都能很好地展示信号频率随时间的变化。

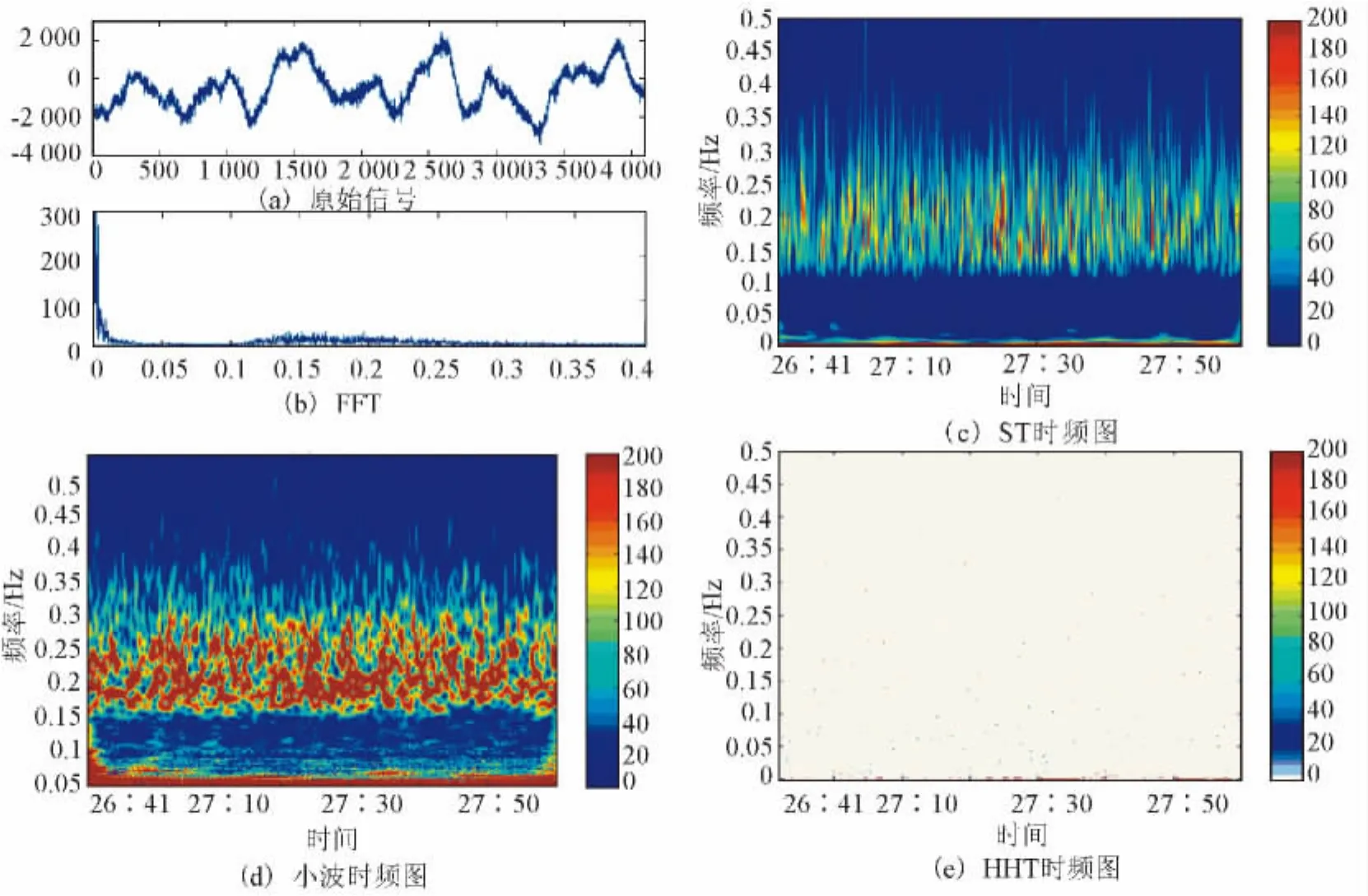
图4 安康台宽频带数据的时频分析比较Fig.4 Comparison of time－frequency analysis based on the broadband data from Ankang station

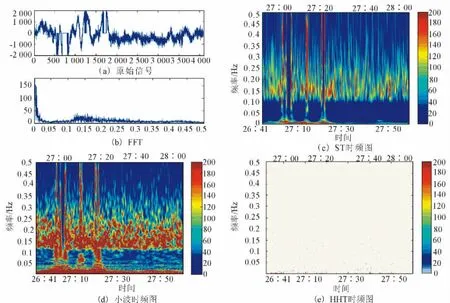
图5 郫县台宽频带数据的时频分析比较Fig.5 Comparison of time－frequency analysis based on the broadband data from Pixian station

（2）由地形变数据的小波变换结果看：小波变换的频谱在低频部分会产生虚假频率信息，但在高频部分的频率分辨率较高，表现为中心频率集中；S变换时间和频率的分辨率都比较好，尤其是在低频部分具有很好的分辨率，但其在高频部分的频率分辨率较低，需要采用必要的方法进行改进，对低频成分比较多的信号S变换优势明显；Hilbert－Huang变换从数据本身进行分解得到，保存了信号本身的物理特性，同时也具有很好的时间和频率分辨率，其频率的分辨率统一，不存在不同频率处分辨率不同的影响，但存在一定的边缘效应，且其和S变换一样受各种条件限制，目前处理的数据量十分有限，同时在揭示趋势变化上存在缺陷，还有待进一步的改进。目前提出的EEMD方法是在Hilbert－Huang变换基础上发展起来的，其使用优势还有待进一步的验证［12］。因此，在对形变数据分析时，针对高频部分可以采用小波分析的方法，低频部分用S变换进行细节分析。分析信号组成成分特征时，可以采用HHT方法将信号进行分解，依次分析各分量的物理特性。

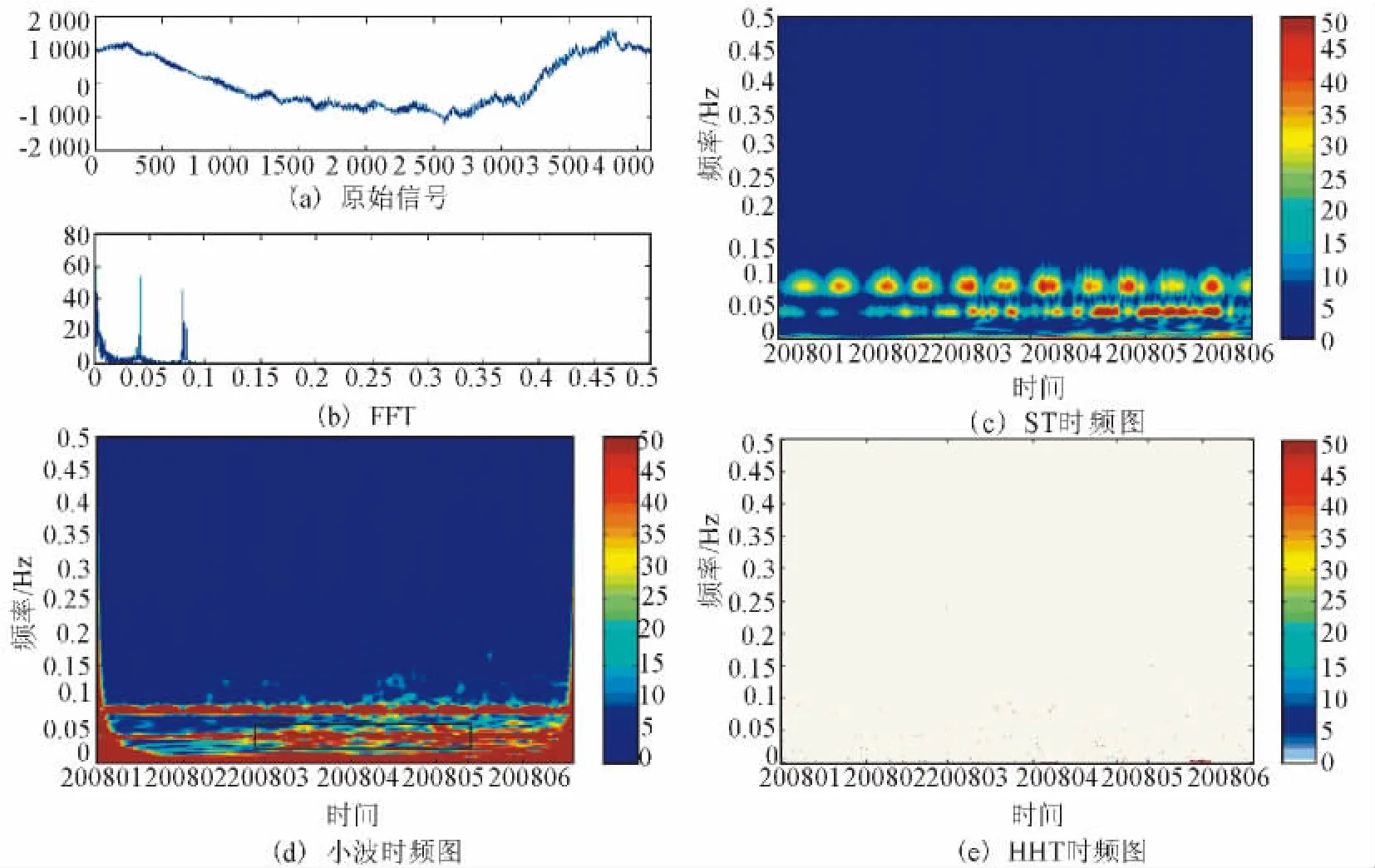
图6 黄梅台应变仪数据时频图比较Fig.6 Comparison of time－frequency analysis based on the strainmeter＇s data from Huangmei station

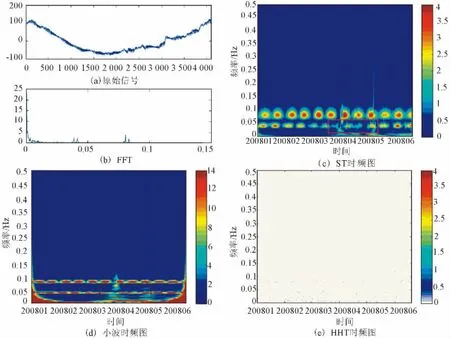
图7 黄梅台倾斜仪数据时频图比较Fig.7 Comparison of time－frequency analysis based on the tiltmeter＇s data from Huangmei station

（3）在针对整时数据的震前后时频分析中，可以看到存在一定的频率异常信号，但其是否属于震前异常，需要进一步的证明。

（References）

［1］杨培杰，印兴耀，张广智.希尔伯特—黄变换地震信号时频分析与属性提取［J］.地球物理学进展，2007，22（5）：1585－1590.YANG Pei－jie，YIN Xing－yao，ZHANG Guang－zhi.Seismic Signal Time－frequency Analysis and Attributes Extraction Based on HHT［J］.Progress in Geophysics，2007，22（5）：1585－1590.（in Chinese）

［2］杨志强，单娜琳，刘占兴，等.S变换在岩溶区地震映像资料处理中的应用［J］.工程地球物理学报，2012，9（2）：227－230.YANG Zhi－qiang，DAN Na－lin，LIU Zhan－xing，et al.Application of S－Transform to Seismic Lmaging Data Processing in Karst Areas［J］.Chinese Journal of Engineering Geophysics，2012，9（2）：227－230.（in Chinese）

［3］杨世锡，胡劲松，吴昭同，等.旋转机械振动信号基于EMD的希尔伯特变换和小波变换时频分析比较［J］.中国电机工程学报，2003，23（6）：102－107.YANG Shi－xi，HU Jin－song，WU Zhao－tong，et al.The Comparison of Vibration Signals’Time－frequency Analysis Between EMD－Based HT and WT Method in Rotating Machinery［J］.Proceedings of the CSEE，2003，23（6）：102－107.（in Chinese）

［4］周挚，山秀明，梁虹，等.固体潮时频分析新方法［J］.地震研究，2005，28（4）：334－339.ZHOU Zhi，SHAN Xiu－ming，LIANG Hong，et al.A New Approach of Earth Tides Time－Frequency Analysis［J］.Journal of Seismological Research，2005，28（4）：334－339.（in Chinese）

［5］周挚，山秀明，张立，等.基于HHT提取昆明，下关重力固体潮的地震前兆信息［J］.地球物理学报，2008，51（3）：836－844.ZHOU Zhi，SHAN Xiu－ming，ZHANG Li，et al.The Gravity Tide of Kunming ＆ Xiaguan Based on the HHT［J］.Chinese Journal of Geophysics，2008，51（3）：836－844.（in Chinese）

［6］吕品姬，赵斌，陈志遥，等.小波分解－STFT方法在地形变观测数据中的应用［J］.大地测量与地球动力学，2011，31（5）：136－140.LV Pin－ji，ZHAO Bin，CHEN Zhi－yao，et al.Application of Wavelet－Decomposition and STFT Method in Continuous Deformation Observation Analysis［J］.Journal of Geodesy and Geodynamics.2011，31（5）：136－140.（in Chinese）

［7］姚家骏，杨立明，冯建刚.常用时频分析方法在数字地震波特征量分析中的应用［J］.西北地震学报，2011，33（2）：105－110.YAO Jia－jun，YANG Li－ming，FENG Jian－gang，et al.Application of Common Time－Frequency Analysis Methods in Analyzing Characteristic Quantity of Digital Seismic Wave［J］.Northwestern Seismological Journal，2011，33（2）：105－110.（in Chinese）

［8］R G Stockwell，L Mansinha，R P Lowe.Localization of the Complex Spectrum：the S Transform［J］.Signal Processing，IEEE Transactions on，1996，44（4）：998－1001.

［9］周竹生，陈友良.含可变因子的广义S变换及其时频滤波［J］.煤田地质与勘探，2011，39（6）：63－66.ZHOU Zhu－sheng，CHEN Yong－liang.Generalized S－transform with Variable－factor and its Time－frequency filtering［J］.Coal Geology ＆ Exploration，2011，39（6）：63－66.（in Chinese）

［10］Huang N E.Lntroduction to the Hilbert－Huang Transform and its Related Mathematical Problems［J］.Lnterdisciplinary Mathematics，2005，（5）：1－26.

［11］武安绪，吴培稚，兰从欣，等.Hilbert－Huang变换与地震信号的时频分析［J］.中国地震，2005，21（2）：207－215.WU An－xu，WU Pei－zhi，LAN Cong－xin，et al.Hilbert－Huang Transform and Time－Frequency Analysis of Seismic Signal［J］.Earthquake Research in China，2005，21（2）：207－215.（in Chinese）

［12］李大虎，梁明剑，黎小刚，等.2011年四川炉霍MS5.3地震加速度记录的时频分析与能量计算［J］.西北地震学报，2013，34（4）：335－341.LI Da－hu，LIANG Ming－jian，LI Xiao－gang，et al.Time－frequency Analysis and Energy Calculation for Acceleration Records of Luhuo MS5.3Earthquake in Sichuan Province in 2011［J］.Northwestern Seismological Journal，2013，34（4）：335－341.（in Chinese）