航空滚动轴承振动信号的小波降噪研究*

吕飞飞，崔凤奎，王晓强，张东英

(河南科技大学 机电工程学院，河南 洛阳 471003)

航空滚动轴承振动信号的小波降噪研究*

吕飞飞，崔凤奎，王晓强，张东英

(河南科技大学 机电工程学院，河南 洛阳 471003)

针对航空滚动轴承振动信号信噪比低且非平稳特性，应用小波理论及小波降噪原理，对航空滚动轴承的振动信号进行小波降噪处理。通过对仿真信号的降噪处理和FFT变换，对比分析了振动信号经过小波降噪及FFT变换和原信号直接进行FFT变换的结果，得到了振动信号小波降噪的有效性。通过对轴承的实测振动信号的降噪处理，进一步表明了小波降噪在消除噪声干扰方面的优越性。

滚动轴承；振动信号；小波理论；降噪

0 引 言

航空滚动轴承既是航空机械系统中必不可少的组成部分，又是航空设备中的薄弱环节，其性能和质量的好坏直接影响航空机械的使用寿命和可靠性[1-2]。统计数据显示，现场实际故障中30%是由于滚动轴承故障而引起的[3]。因此，开展对滚动轴承的缺陷故障诊断具有很重要的意义。在轴承的缺陷故障诊断中，航空滚动轴承自身缺陷故障信号是非平稳时变信号，持续时间极短，所获得的振动加速度信号一般都很微弱，通常被淹没在很强的背景噪声和轴承其他部件振动信号中。在测量振动信号的时候，由于测量系统本身的特性又引入了其它噪声和干扰，使信噪比再次下降[4]。如何有效去除噪声，是后续提取信号特征向量的前提[5]。

在振动信号的降噪方面国内外有一定的研究。Fourier提出的傅里叶变换[6-7]将信号从时间域转换到频率域，能够很好地满足分析要求，但是在进行FFT变换的时候丢掉了时间信息，不能判断信号发生的时间。Gabor在傅里叶变换基础上提出的Gabor变换[8]能够反映出信号的局部特征，但是其窗函数的大小和形状均与时间和频率无关而保持不变，不利于同时对高低频信号进行分析。

小波变换[9-10]是时间窗和频率窗都可改变的时频局部化分析方法，能在做变换的时候对时间和频率的兼顾。通过使用小波变换分析方法，对轴承振动信号进行降噪分析，得到了较好的效果。笔者通过小波变换理论，采用阈值处理降噪算法，对模拟信号及滚动轴承振动信号进行消噪。

1 小波理论及阈值处理算法

1.1 小波变换理论

平方可积函数f(t)即[f(t)∈L2(R)]的小波变换定义为[11]：

a,b∈R,a>0

(1)

1.2 小波阈值降噪处理算法

基于阈值处理的小波降噪算法是一种直观而有效的去噪算法[12]。设原始信号为f(k)其长度为N，加入噪声信号e(k)的含噪信号为s(k)，噪声强度为ε，噪声的方差为σ2，于是一个含噪声的一维信号的模型可以表示成如下的形式[13]:

s(k)=f(k)+ε×e(k),k=0,1,…n-1

(2)

对式(2)进行小波域变换，可得X=Wx，W为小波变换矩阵。对信号进行小波分解后，噪声小波系数的平均功率与尺度成反比，其幅度随着小波分解层数的增加而不断减小，其能量分散于大量的小波系数上，且白噪声的小波系数仍是白噪声。 有用信号经小波变换后，其能量被压缩到相对较少而数值较大的小波系数上。通过设定阈值使较小的系数为0，可较好地去除噪声，得到信号的估计值：

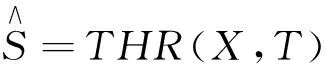
(3)

算法中常用的阈值处理有硬阈值方法和软阈值方法两种。阈值选择方法一般是在高斯白噪声的前提下提出的，考虑到实际噪声在小波域不同尺度上的差别 可采用以下基于尺度的阈值方法，对不同尺度选择不同的阈值，即:

(4)

式中：MADj是尺度j上小波系数中值的绝对值；N是含噪信号的长度。

在小波消噪过程中，根据具体应用来选择一种合适的阈值来达到理想的去噪效果。

1.3 信号的小波降噪过程

小波变换运用在信号降噪处理中，主要是针对信号经小波变换后在不同分辨率下呈现不同规律，在不同分辨率下设定不同阈值门限，调整小波系数，达到降低噪声的目的。降噪算法如下。

(1) 信号的小波分解。选择一个小波，并确定小波分解的层次N，然后对信号进行N层小波分解。

(2) 小波分解高频系数的阀值量化。从第1层到第N层的每一层高频系数选择一个阈值进行阈值量化处理。

(3) 信号的小波重构。根据小波分解底层低频系数和各层高频系数，进行信号的小波重构。

2 仿真信号的降噪处理

振动位移曲线的波形是类似正余弦的周期性信号，所以选取正弦信号来进行仿真[14-15]。图1(a)为附加噪声的正弦信号，图1(b)是对噪声信号进行傅里叶变换得到的频谱图，图1(c)是对加噪信号采用小波分解处理后的降噪信号进行傅里叶变换得到的频谱图。从图1可以看出，原始信号受噪声影响比较严重，规律性比较差。对该信号进行频谱分析的结果能从一定程度上反映基频，但是存在一部分的噪声。对原始信号进行降噪后的信号消除了噪声，呈现了明显的规律性，且频谱分析结果表明降噪前后的基频是一致的，由此表明小波降噪能够有效的对振动信号进行降噪处理，准确的反映基频大小。

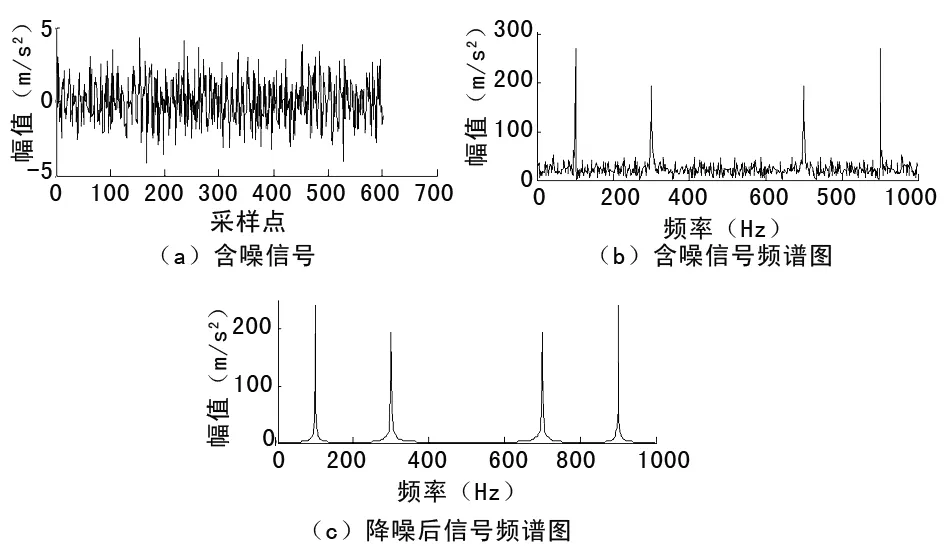
图1 仿真信号的降噪处理

3 滚动轴承振动信号降噪分析

利用小波降噪分析对实际的航空滚动轴承实际振动信号进行降噪处理。搭建试验台，电机通过皮带带动主轴正常旋转，从而带动轴承内圈以相同频率旋转。选用71903AC角接触球轴承，电机额定功率2 kW，额定转速1 350 r/min，采样频率为3 kHz。图2(a)是实验测得的外圈故障轴承振动时域信号，图2(b)为该振动信号的频谱图；图2(c)是利用小波降噪方法采用dB6小波、minimax阈值模式对故障轴承振动信号经过5层小波分解得到的降噪信号；图2(d)为小波降噪信号的频谱图。

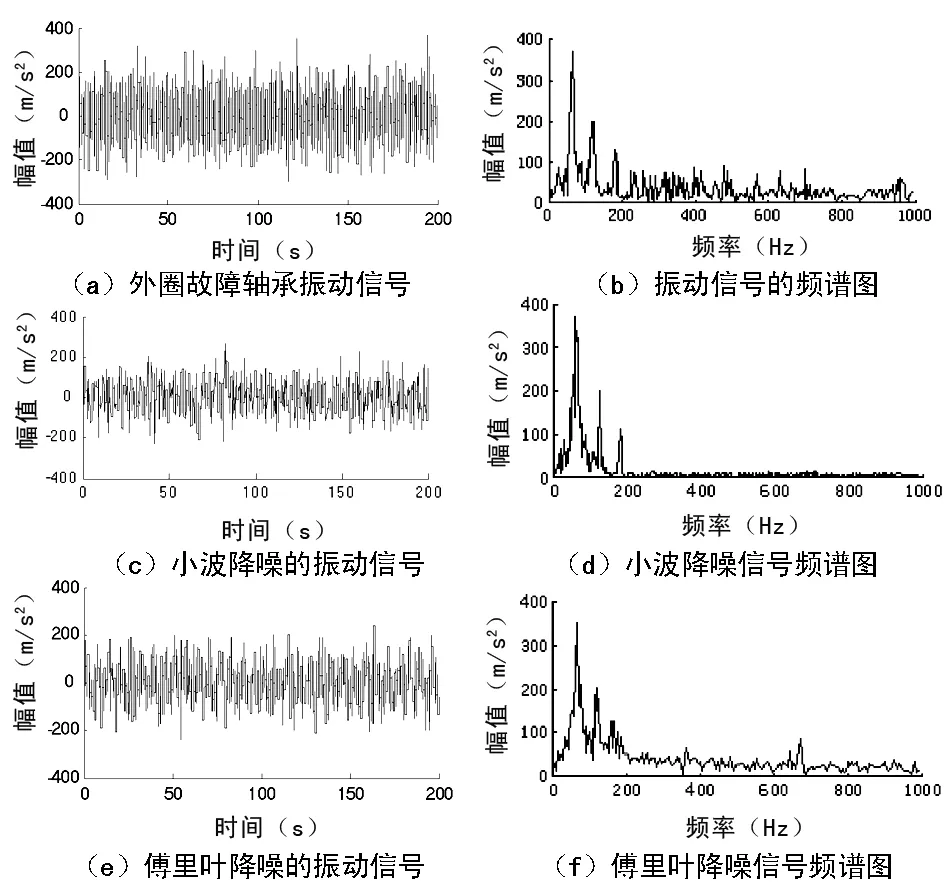
图2 外圈故障轴承振动信号处理

图2(e)是采用傅里叶降噪方法对故障轴承振动信号进行处理得到的降噪信号，图2(f)为傅里叶降噪信号的频谱图。

比较图2各图中可以看出，用小波变换对信号进行降噪很好地保留了尖峰和突变部分，可以将信号的高频部分和噪声引起的高频干扰有效地区分，而用傅里叶方法进行降噪时，利用的是低通滤波器进行滤波，即认为信号集中在低频部分而噪声集中在高频部分，若低通滤波器太宽则滤波后，大量噪声仍包含在信号中，若低通滤波器太窄，则可能把一些有用的信号滤掉，而且无法区分信号的高频部分和噪声的高频部分。因此，小波变换降噪方法优于傅里叶降噪方法。

对内圈故障的航空滚动轴承进行振动测试，测试结果如图3所示。信号的采样频率为2 kHz。选用6 308深沟球轴承，采样频率为2 kHz。图3(a)是测得的内圈故障轴承的振动时域信号，图3(b)为对内圈故障轴承振动信号进行小波降噪后的降噪信号，该降噪信号是采用db6小波、minimax阈值模式处理，对信号进行5层小波分解得到的时域信号。

图3 内圈故障轴承振动信号处理

从图3(a)和图3(b)的对比可知，采用小波理论降噪后的时域信号，在很大程度上能够抑制噪声的影响，保留原始信号的尖峰和突变成分，提高了信噪比，使冲击响应特性更突出，便于信号特征向量的提取。因此，小波分析对非平稳信号降噪有不可比拟的优点。

4 结 论

从理论上分析了小波降噪的原理，用数字仿真及实测信号的方法证明了小波降噪具有如下优越性能。

(1) 小波分析能够准确地对动态信号进行降噪处理，消除干扰噪声，获得比较真实的振动信号，且无信号失真现象。

(2) 针对振动试验中的其它振动信号也可用小波分析的方法进行滤波降噪，以得到真实反映振动特性的信号，为分离与缺陷有关的信号及典型缺陷特征向量的提取提供了可靠的依据。

(3) 在振动信号降噪方面，小波变换优于傅立叶变换，通过调节小波分解的层数及其阈值的大小来达到满意的降噪效果，既能反映振动特性又保留了信号的高频部分特性。本文针对模拟信号与实测信号的小波降噪处理具有一定的实际应用价值和现实意义。

[1] 赵鲁宁,孙 颖. 航空发动机主轴轴承故障诊断 [J]. 飞机设计,2010,30(2):46-50.

[2] 韩 磊,洪 杰,王 冬. 基于小波包分析的航空发动机轴承故障诊断 [J]. 推进技术,2009,30(3):328-332

[3] 杨文平. 基于小波理论的复杂机械振动信号降噪分析 [J]. 北京科技大学学报,2002,24(4):455-457.

[4] 朱振军. 轴承振动故障分析 [J]. 设备管理与维修,2011(1):99-100.

[5] 刘正平,冯召勇,杨卫平. 基于小波去噪的微弱信号提取 [J]. 制造业自动化,2010,32(8):98-101

[6] 潘文杰. 傅里叶分析及其应用 [M].北京:北京大学出版社,2002.

[7] 费佩燕,刘曙光. 小波分析应用的进展与展望 [J]. 纺织高校基础科学学报,2001,14(1):72-78.

[8] 何继爱,裴承全,浦阳阳. 信号分析与处理的方法研究[J].无线通信技术,2012(2):12-15.

[9] 张小英. 小波分析在一维信号处理中的应用及发展 [J]. 内江科技,2012(1):47-50.

[10] 何 斌,戚佳杰,黎明和. 小波分析在滚动轴承故障诊断中的应用研究 [J]. 浙江大学学报(工学版),2009, 43(7):23-26

[11] 朱来东,廉小亲,江远志. 小波变换在信号降噪中的应用及MATLAB实现 [J]. 北京工商大学学报,2009,27(2):46-49.

[12] 蔡 铁,朱 杰. 小波阈值降噪算法中最优分解层数的自适应选择 [J]. 控制与决策,2006,21(2):217-220.

[13] 王秉仁,杨艳霞,蔡 伟,等. 小波阈值降噪技术在振动信号处理中的应用 [J]. 噪声与振动控制,2008, 28(6):9-12.

[14] 崔玉敏. 基于振动信号非线性方法的轴承故障诊断研究 [D]. 镇江:江苏大学,2010.

[15] 李曙光，张梅军，陈江海.基于小波包和分形盒维数的滚动轴承故障诊断[J].机械，2010(8)：21-23.

Research on the Wavelet De-noising of Vibration Signals for Aircraft Rolling Bearings

LV Fei-fei, CUI Feng-kui, WANG Xiao-qiang, ZHANG Dong-ying

(CollegeofMechanicandElectronicEngineering,HenanUniversityofScienceandTechnology,LuoyangHenan471003，China)

Aiming at air rolling bearing vibration signals low SNR and non-stationary characteristics, taking wavelet theory and principles of the wavelet noise reduction for air vibration signals of rolling bearings to conduct wavelet noise reduction processing. By means of the simulation signal wavelet noise reduction processing and fast Fourier transform, the contrast analysis of the vibration signals is made after wavelet noise reduction and FFT transform and the original signal directly to the result of the fast Fourier transform, and thus the validity of the vibration signal wavelet noise reduction is proved. Through the actual vibration signals of bearing conduct noise reduction processing, the result is a further indication of the superiority of wavelet noise reduction in eliminate noise interference.

rolling bearings；vibration signals；wavelet theory；de-noising

2014-03-06

国防军工技术基础科研项目(编号：科工技[2011]869号)

吕飞飞(1987-)，女，河南平顶山人，硕士，主要从事高速精密加工技术与精密测试方法方面的研究工作。

TH133.3

A

1007-4414(2014)02-0089-03