双序置换的最长递增子列

崔汉哲

（上海电机学院 数理教学部，上海201306）

长久以来，置换因其丰富的组合结构与代数结构一直是组合数学与代数学的重要研究对象。置换研究中的某些问题还与其他一些似乎联系不大的数学分支有关，最长递增子列便是一例。

最长递增子列的研究最早由Ulam于20世纪60年代初提出，研究的核心问题是其长度在随机置换中的渐进分布[1]。经过近40年的发展，Baik等[2]于1999年证明了在一般随机置换中，最长递增子列长度的渐进分布为Tracy-Widom分布；期间，除组合学和代数学外，他们还运用了分析学、概率论、算子理论、微分方程、特殊函数、表示论等数学分支的知识和方法。而Baik等[3-4]研究的重要成果证明了在组合学与随机矩阵理论之间存在着紧密的联系，并引发了学者们进一步的研究兴趣。

除在一般置换中研究最长递增子列外，某些特殊置换中的情形也受到了关注[5-11]，其中，渐进分布仍然是研究的重点。而本文对一类特殊置换的研究表明，其最长递增子列长度的分布概率可以被精确计算。方法是先将该类置换与另一基本的组合对象——杨氏表（Young Tableau）建立联系，然后利用杨氏表的计数方法来完成。

1 定义与引理

本文中，长度为n的置换π表示为其中＝ ｛1，2，…，n｝ ，i＝1，2，…，n，且两两不同。

定义1 若置换中有，且i1＜i2＜…＜ik，则称为π的一个长度为k的递增子列。所有递增子列中长度最大者称为的最长递增子列。递减子列的定义完全类似。

定义2 若长度为2n的置换满足则称其为双序置换（2-Ordered Permutation）。

显然，所有长度为2n的双序置换的个数为二项式系数其最长递增子列长度的可能取值为n，n＋1，…，2n。本文研究的主要问题实质是，在所有长度为2n的双序置换中，最长递增子列的长度为n＋k（k＝0，1，…，n）的置换个数。不同于一般置换中的情形，该数在双序置换中可以被精确计算。为此要在置换与杨氏表间建立联系。杨氏表的定义、基本术语和性质可参见文献[12-13] 。本文利用在置换与杨氏表的二元组（P，Q）之间建立一一对应的Robinson-Schensted-Knuth算法（简称为 RSK 算法）[12-13]。

引理1 所有长度为2n的双序置换与所有行数为1或2的杨氏表（元素个数2n）之间存在一一对应关系。在该对应关系之下，最长递增子列长度为n＋k的置换恰好对应第1行长度为n＋k的杨氏表。

证明 记双序置换杨氏表二元组（P，Q）中P的第1行为x1x2…xn＋k，第2行为y1y2…yn-k，（k∈[n] ∪｛0｝）。

首先建立一一对应关系。从长度为2n的双序置换到行数为1或2的杨氏表的映射f即为RSK算法中，由置换生成杨氏表二元组（P，Q）中的P。RSK算法的性质说明的最长递减子列长度恰为杨氏表二元组（P，Q）中P的行数，即第1列的长度[8] 53。当为双序置换时的最长递减子列长度最多为2，故此时生成的杨氏表行数为1或2。且容易验证，此时，RSK算法有十分简单的形式，其算法步骤如下：

步骤1 令

步骤2 当m＝2n＋1时，算法停止，此时得到的杨氏表即为f（π）；否则

（1）若πm＞xi，则令xi＋1＝，再令i＝i＋1，m＝m＋1，返回至步骤2；

（2）若，则令，再令j＝j＋1，m＝m＋1，返回至步骤2。

例：设＝1 3 2 5 4 6，则f）的第1行为1 2 4 6，第2行为3 5。

为构造的逆映射g，本文分析中两行元素的构成。由上述算法的步骤2与双序置换的定义，可验证f（π）的第2行元素为中所有满足的从左到右依次排列而成的其余元素依次排列为的第1行。由此，可得f（π）的逆映射g，即从行数为1或2的杨氏表生成双重序列置换的算法如下：

步骤1 令i＝n＋k，j＝n-k，m＝2n。

步骤2 当m＝0时，算法停止，此时得到的即为g（P）；否则

（1）若yj＜xi，则令＝xi，再令i＝i-1，m＝m-1，返回至步骤2；

（2）若yj＞xi，则令＝＝yj，再令i＝i-1，j＝j-1，m＝m-2，返回至步骤2。

由f与g的互逆性保证g（P）为一个双序置换，于是一一对应关系建立。

RSK算法的性质说明，在上述对应关系下，P的第1行长度，即列的个数恰为π的最长递增子列长度[13] 99。 证毕。

2 定理及其证明

本文采用随机置换的语言叙述定理。一个随机双序置换是指在所有双序置换中等可能随机选取的置换。令Ln为长度为2n的随机双序置换中最长递增子列的长度。

定理1Ln的分布为

期望为

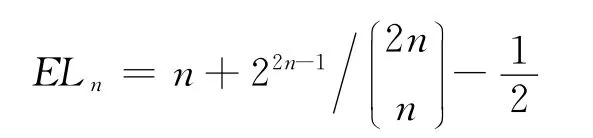
方差为

证明 为求P（Ln＝n＋k），只需计算所有长度为2n的双序置换中，最长递增子列长度为n＋k的置换个数。而根据引理1，这恰是所有1行与2行的杨氏表中，首行长度为n＋k的杨氏表个数。为此，本文用计算杨氏表个数的钩形公式[12-13]，该数为

由此可得P（Ln＝n＋k）。

为求Ln的期望与方差，先计算

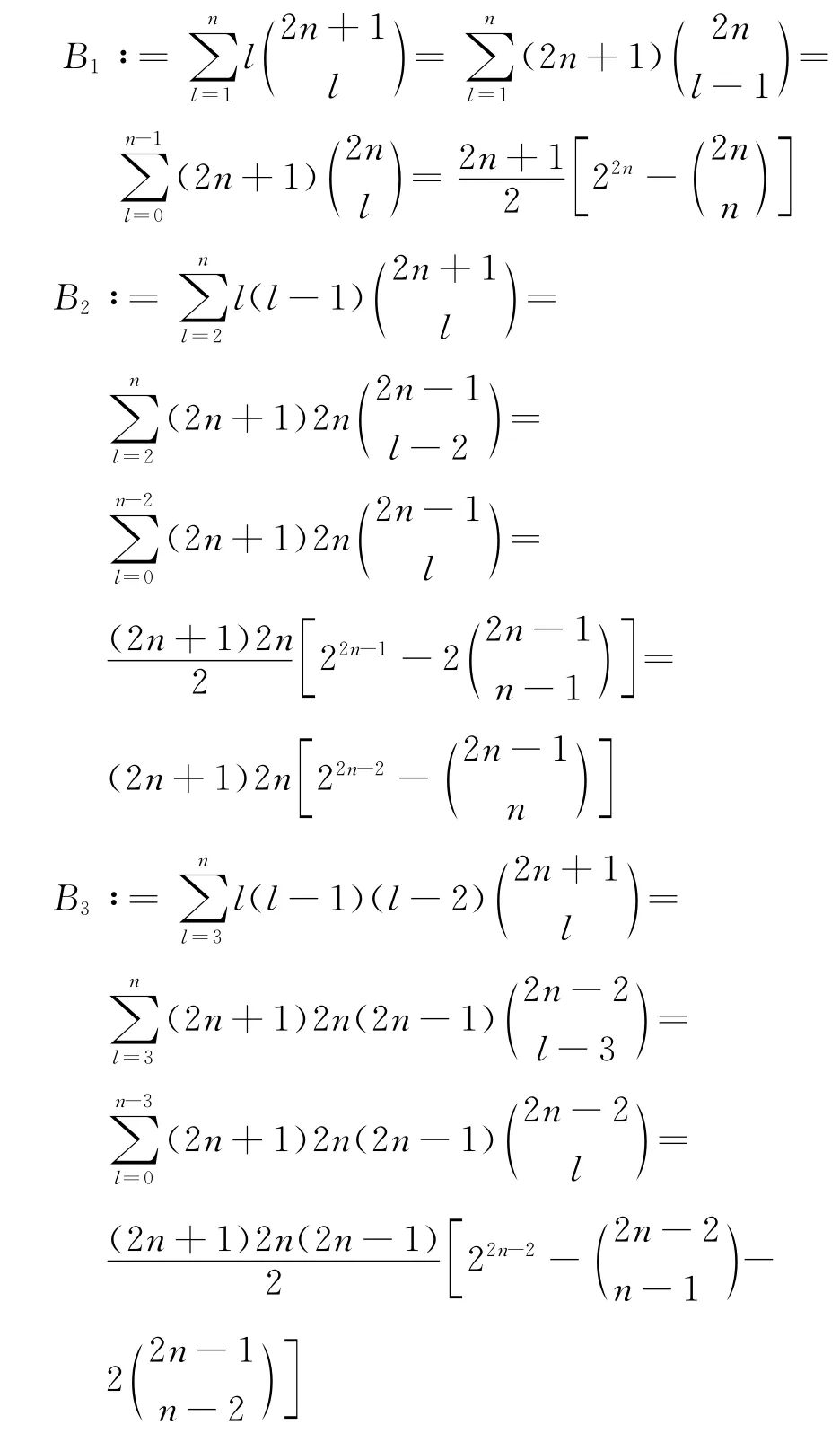
于是，

由于再将B1、B2代入，化简便得

故

类似地，有

令l＝n-k，则

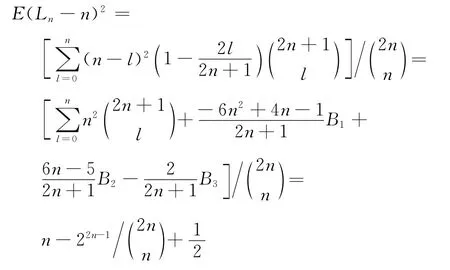
故Ln的方差

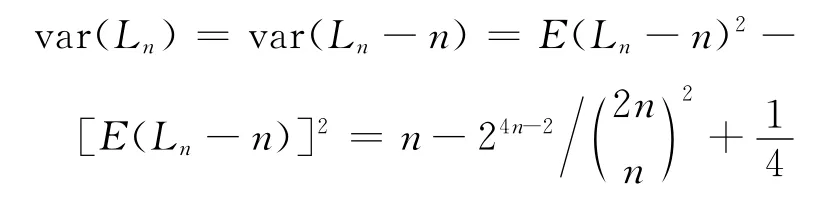
证毕。

作为上述定理的一个简单应用，可以求出双序置换的另外一个重要统计量——下降数的分布。在置换中，若，则称i为π的一个下降。中所有下降的个数称为的下降数，记为在所有长度为n的置换中，下降数为k的置换个数为欧拉数（Eulerian Number）A（n，k＋1）[14-15]。而对于双序置换，下降数与最长递增子列的长度有如下关系。

性质1 当为长度2n的双序置换时，2n-为其最长递增子列的长度。

证明 若中有则显然与不能同时出现在递增子列中。另一方面，引理1中对映射f的分析说明，将所有的下降i处的删除后，余下元素即组成的一个最长递增子列。

证毕。

令Dn为长度为2n的随机双序置换的下降数，则由Dn＝2n-Ln和定理1可得：

推论1Dn的分布为

期望为

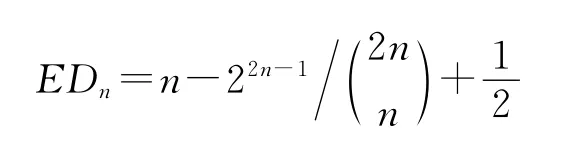
方差为

3 结 语

本文在双序置换与一类杨氏表之间建立一一对应关系，从而给出随机双序置换中最长递增子列长度的分布。一直以来，最长递增子列的核心问题是渐进分布，于是自然存在如下问题：当n→∞时，Ln的渐进分布为何，它是否为某个已知随机变量的分布函数，该分布函数在概率论或随机矩阵理论中是否已经有比较重要的应用等都有待进一步研究。

[1] Ulam S M.Monte Carlo calculations in problems of mathematical physics[J] .Modern Mathematics for the Engineer，1961：261-281.

[2] Baik J，Deift P，Johansson K.On the distribution of the length of the longest increasing subsequence of random permutations[J] .Journal of the American Mathematical Society，1999，12（4）：1119-1178.

[3] Baik J，Deift P，Johansson K.On the distribution of the length of the second raw of a Young diagram under plancherel measure[J] .Geometric and Functional Analysis，2000，10（4）：702-731.

[4] Stanley R P.Increasing and decreasing subsequences and their variants[C] ∥Proceeding of the International Congress of Mathematicians.Madrid：[s.n.] ，2007：545-579.

[5] Pittel B.Romik D.Limit shapes for random square Young Tableaux[J] .Advances in Applied Mathematics，2007，38（2）：164-209.

[6] Romik D.Arctic circles，domino tilings and square Young Tableaux[J] .The Annals of Probability，2012，40（2）：437-891.

[7] Odlyzko A M，Rains E M.On longest increasing subsequences in random permutations[J] .Contemporary Mathematics，2000，251：439-452.

[8] Bespamyatnikh S，Segal M.Enumerating longest increasing subsequences and patience sorting[J] .Information Processing Letters，2000，76（1）：7-11.

[9] Albert M H，Golynski A，Hamel A M.Longest increasing subsequences in sliding windows[J] .Theoretical Computer Science，2004，321（2-3）：405-414.

[10] Albert M H，Atkinson M D，Nussbaum D.On the longest increasing subsequence of a circular list[J] .Information Processing Letters，2007，101（2）：55-59.

[11] Chen Erdong，Yang Linji，Yuan Hao.Longest increasing subsequences in windows based on canonical antichain partition[J] .Theoretical computer science，2007，378（3）：223-236.

[12] Stanley R P.Enumerative Combinatorics：Vol.1[M] .2nd ed.Cambridge：Cambridge University Press，2011：38.

[13] Sagan B E.The symmetric group：Representations，Combinatorial Algorithms，and Symmetric Functions[M] .2nd.ed.[s.L.] ：Springer-Verlag，New York Inc，2001：53，99.

[14] Stanley R P.Enumerative Combinatorics：Vol.2[M] .Cambridge：Cambridge University Press，1999：316.

[15] Bona M.Combinatorics of Permutations[M] .[s.L.] ：Chapman ＆ Hall／CRC，2012：5.