Effects of Airflow Field on Droplets Diameter inside the Corrugated Packing of a Rotating Packed Bed

Xu Chengcheng; Jiao Weizhou; Liu Youzhi; Guo Liang; Yuan Zhiguo; Zhang Qiaoling ()

Effects of Airflow Field on Droplets Diameter inside the Corrugated Packing of a Rotating Packed Bed

Xu Chengcheng; Jiao Weizhou; Liu Youzhi; Guo Liang; Yuan Zhiguo; Zhang Qiaoling (Shanxi Province Key Laboratory of Higee-Oriented Chemical Engineering, North University of China, Taiyuan 030051)

Rotating packing bed (RPB) has a better mixing performance than traditional mixers and shows potential application in the petroleum industry. However, acquisition of information about the mixing process directly through experiments is difficult because of the compact structure and complex multiphase flow pattern in RPB. To study the mixing characteristic, Fluent, the computational fluid dynamics (CFD) software, was used to explore the effect of airflow field on droplet diameter. For conducting calculations, the gas-liquid two-phase flow inside the packing was simulated with the RNGk-ε turbulence model and the Lagrange Discrete Phase Model (DPM), respectively. The numerical calculation results showed that coalescence and breakup of droplets can take place in the gas phase flow inside the packing and can be strengthened with increased rotating speed, thereby leading to the enlargement of the average diameter.

rotating packed bed; computational fluid dynamics; gas-liquid flow field; diameter; mixing

1 Introduction

Rotating packed bed (RPB), a new process-intensification equipment, can greatly intensify the gas-liquid mass transfer efficiency by means of strong centrifugal acceleration, which has been excellently applied in several petroleum processes, such as petrochemical wastewater treatment[1-3], gas treatment[4-5], and petrochemical production[6-7]. Recently, it has been extended to the intensified mixing processes, such as the preparation of emulsified diesel[8-12], paraffin wax[13], petroleum sulfonate[14], etc. However, the mixing mechanism inside RPB is seldom reported because of the following reasons: (1) The mixing behavior of droplets inside packing is too difficult to be observed by experiments[15]because of the compact structure of packing in RPB and the shielding effect between packing and droplets; (2) The flow pattern of RPB is a complex gas-liquid two-phase flow, which is different from that of the traditional mixer with a single-phase flow. Specifically, the liquid is dispersed to form a large number of fine droplets in the continuous gas phase flow[16], which can coalesce and break up upon passing through the packing to complete the mixing process. Moreover, the gas phase flow is accompanied by rotational packing with high speed[15], which has an important effect on droplet coalescence and breakup[17]. Consequently, the complex fluid dynamic characteristics of RPB make it difficult to describe mixing process by using classical mixing theory. The most significant difference of mixing processes between RPB and traditional mixer is that the gas phase flow has an effect on droplets coalescence and breakup in RPB. As it is well known, CFD is a powerful tool to simulate several phenomena that cannot be easily observed by experiments directly[18-20], which provides a new way to investigate the mixing behavior inside RPB. The computational fluid dynamics (CFD) and multiphase flow theory were used to explore the effect of gas phase flow on droplet diameter during the intensified mixing process of RPB. In our study, the rotational speed is used as variables to investigate the change in droplet diameter, because the change in the gas phase flow field is mainly caused by rotational speed. In calculations, the change in droplet diameter caused by shearing action of packing is not taken into account, which will be investigated in the future work. Thus, the droplets may only be assumed to be rebounded by packing after colliding with the packingsurface, i.e., the change in droplets size is affected by gas phase flow via two processes: (1) the collision between the droplets; and (2) the deformation, tension, and breaking of droplets in the gas phase flow field.

2 CFD Simulations

2.1 Mathematical model

The gas-liquid flow was simulated using CFD codes, RNGk-εturbulence model to describe the gas phase, and the Lagrange Discrete Phase Model (DPM) to analyze the change in droplet diameter. The RNGk-εturbulence model had been successfully used to describe the continuous phase in RPB[21]. In DPM, the dispersed phase is simulated by tracking a large number of droplets through the calculated continuous phase. When simulating droplet collisions and their outcome, calculating the possible intersection of many droplets would still be expensive. Fluent uses an effective algorithm of O’Rourke[22]to describe the number of droplet collisions and their outcome. Accordingly, the concept of parcels can be used, which are statistical representation of a number of individual droplets. Once two parcels of droplets collide, the algorithm could further determine the type of collisions, and the result of collisions can only be coalesced or rebounded. In this paper, two classic methods are used to calculate the breakup of droplets: the Taylor Analogy Breakup (TAB) model[23]and the wave model[24]. The TAB model is recommended for low Weber numbers, and when the Weber number is greater than 100, the wave model is more suitable[25].

2.1.1 Collision and droplet coalescence model

The probability of collision between two droplets is taken from the point of view of the larger droplet, which is called the collector droplet. Once two parcels collide, the result of collision must be as follows. If the droplets collide head-on, the result tends to be a coalescence; if the collision is more oblique, the result tends to be a rebound. The criterial equation can be expressed as follows:

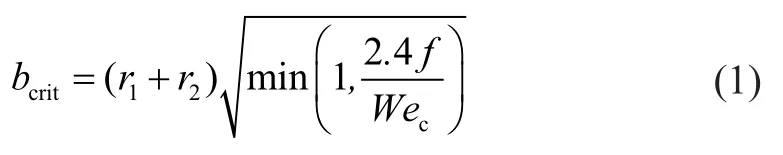
The criterial equation is a function of the collisional Weber numberwhileandare the radii of the bigger droplet and the smaller droplet, respectively.is defined by Equation (2).

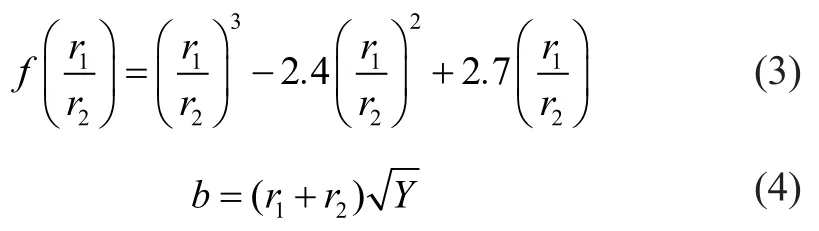
The actual collision parameterbis expressed by Equation (4), whereYis a random number between 0 and 1. Ifthe coalescence occurs as a result of collision, then the properties of the coalesced droplets are found from the basic conservation law. In the case of a grazing collision, the new velocities are calculated based on conservation of momentum and kinetic energy. A fraction of kinetic energy of droplets is assumed to be lost because of viscous dissipation and generation of angular momentum. Finally, the new velocity after collision can be expressed by Equation (5).

2.1.2 Breakup model theory

The non-dimensional equation of TAB model can be expressed as follows:

whereyis a dimensionless variable, which is defined by Equation (7), andandare the density of discrete phase and continuous phase, respectively,uis the relative velocity of droplets,ris the radius of undisturbed droplets,σis the surface tension of droplets, andlis the viscosity of droplets. The dimensionless constants include:

In Equation (7),xis the displacement of the droplet equator from its spherical position. If, the droplets would break up, and then the radius of the newly formed child droplets can be calculated by Equation (8).

whereKis the ratio of total energy of distortion and oscil-lation to the energy, which is generally equal to 10/3.

As regards the Wave model, it is assumed that the radius of the newly formed dropletsis proportional to the wavelength of the fastest-growing unstable surface wave. And it can be expressed by Equation (9).

whereOhis the Ohnesorge number andTais the Taylor number. They can be respectively defined by Equations (11) and (12), in whichandare the liquid and gas Weber number, respectively, andis the Reynolds number.

The change of radius of droplets in the parent parcel can be obtained from Equation (13).

The breakup timeτis given by Equation (14).

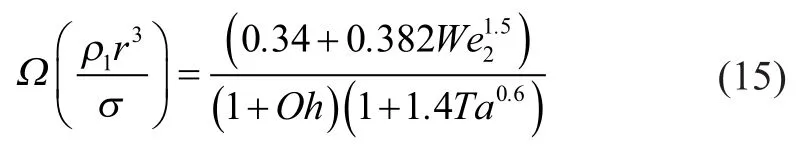
2.2 Geometrical model and mesh generation

A sketch of a typical RPB, which is used to intensify the mixing process, is shown in Figure 1. A number of fine droplets is formed by the liquid from the impinging stream distributor and has an average diameter 0.98 mm. The droplets are then injected into the packing of RPB with a high velocity. The packing layer is generally composed of a multi-layer wire mesh packing in the shape of concentric annulus, and the structure of the wire mesh packing consists of the latitudinal and longitudinal wires. Because of the restriction of computer performance, the packing geometrical model was simplified to be twodimensional, as shown in Figure 2. In that model, a single wire with a diameter of 0.5 mm was simplified as a square with a side length of 0.5 mm. The arrangement of simplified packing is presented in Figure 3. The center distance between two adjacent layers of packing in radial direction and the center distance between two adjacent packing wires in the circumferential direction are both 1.5 mm[15]. Moreover, the independence of meshes was also verified, and a mesh containing at least 153 666 cells was required to resolve the 2D flow field sufficiently.

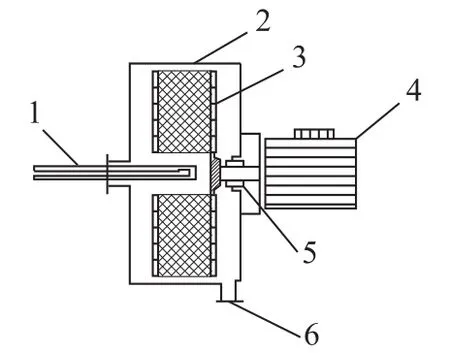
Figure 1 The structural scheme of RPB

Figure 2 The 2D physical model diagram of packing

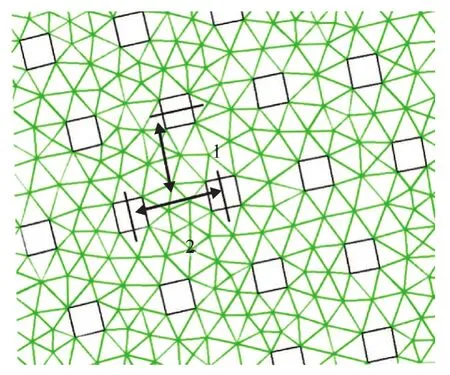
Figure 3 The partial schematic illustration of the packing arrangement

2.3 Boundary conditions

The initial volume fraction of the gas phase flow was specified as 1 in the packing, and the injection type ofliquid inlet was assumed to be surface injections with a velocity of 0.5 m/s. The initial average diameter of the droplets was set at 0.98 mm. The packing area, which is defined as the rotating zone, was solved in a moving reference frame (MRF), and the rotational speed was in the range of between 300 r/min and 1 200 r/min. For all samples, the packing surface was set at a moving wall surface condition, specified at 0 r/min relative to the adjacent cell zone and the shear condition was assumed to be slip free. Moreover, in DPM condition the outer side, inner side, and surface of the packing were specified as trapping, escaping, and reflecting from the boundary, respectively.

A double precision mode was used to simulate the process of changes in size of droplets, and the SIMPLE algorithm was used to deal with the pressure-velocity coupling. Solver’s type, velocity formulation, time, and 2D space were assumed to be pressure-based, absolute, steady, and planar, respectively. A second-order upwind scheme was selected for gradient, pressure, momentum, turbulent kinetic energy and turbulent dissipation rate, and a residual error down to 1×10-4in precision was considered as the model convergence. Based on the unsteady particle tracking, the collision, coalescence, and breakup model was selected. In our study, the coupled calculations procedure was used to simulate the gas-liquid two-phase flow. The continuous phase was performed five times after each iteration of the discrete phase.

3 Experimental

Our objective is to investigate the effect of gas phase flow inside the packing on the droplet diameter in a RPB. However, excluding the effect of shear effects on the droplet and creating the same gas flow field for investigation in the actual experiment are difficult. So the porosity of the packing was reduced to approximately simulate the flow field, and the packing arrangement is shown in Figure 4. The packing was composed of six groups of metal wires, with four metal wires in each group (with a height of 100 mm, and a diameter of 3 mm), and the radial distance between two adjacent wires is 5 mm. The experimental procedure is shown in Figure 5. The information of droplets was obtained using a CCD camera with macrolens of particle image velocimetry system (TSI Inc.).

The droplet diameter was too difficult to be measured accurately because the light was shaded by rotational wires. Therefore, the information of droplet diameter at the outer boundary of the packing was recorded.

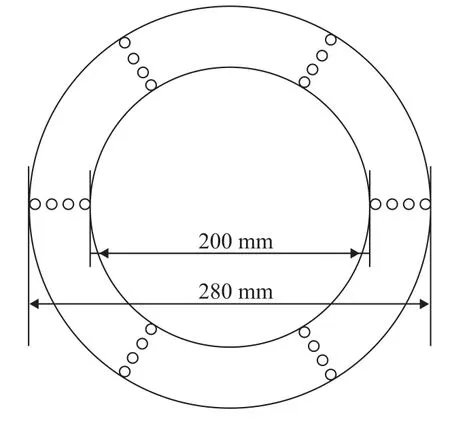
Figure 4 Experimental packing arrangement

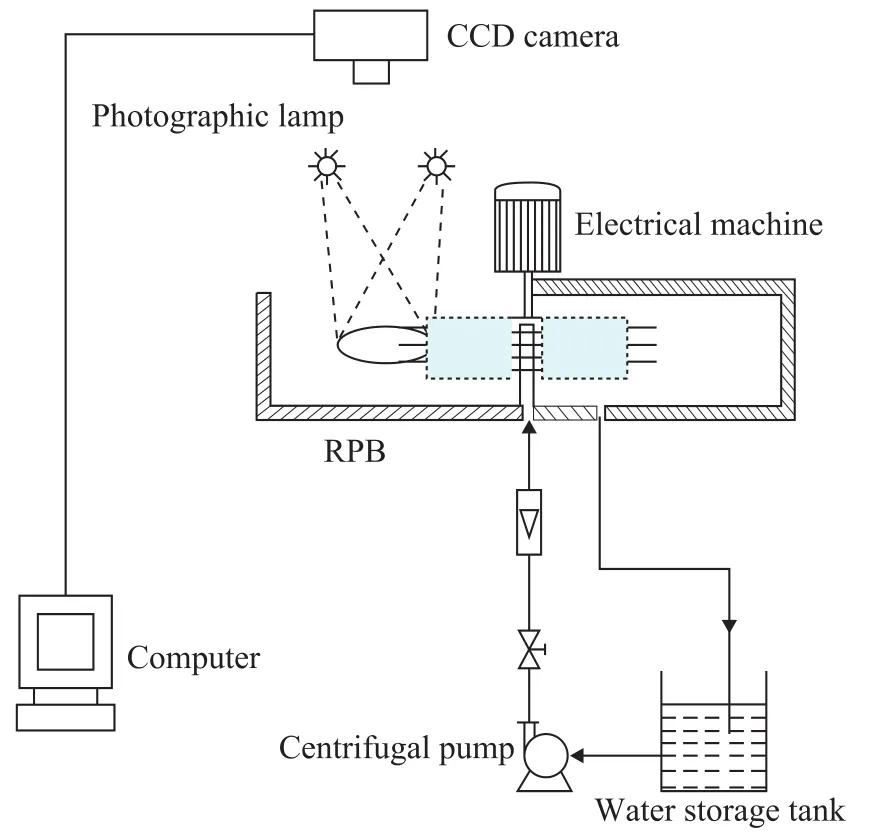
Figure 5 Experimental set-up

4 Results and Discussion

4.1 Effect of rotational speed on droplets’ Weber number

The effect of rotational speed on Weber number is given in Figure 6. The Weber number is defined as the ratio of inertial force to surface tension, which directly affects the process for breaking of droplets. As shown in Figure 6, the Weber number increased with an increasing rotational speed. The Weber number could go up to 6 000 when the speed was about 1 200 r/min. At the same time, the fluctuation of Weber number was more obvious, which might be caused by the change in diameter arising from the co-alescence or breakup of droplets. Meanwhile, the Weber number increased remarkably when the time of droplets’movement was increased at the same rotational speed. This result was mainly attributed to the increased circular velocity from the inner space to the outer edge[15]. Moreover, it can be seen from Figure 6 that the residence time of droplets was very short (0.03 s to 0.1 s) and decreased with an increasing rotational speed, which was similar to the results reported by Shi[26].

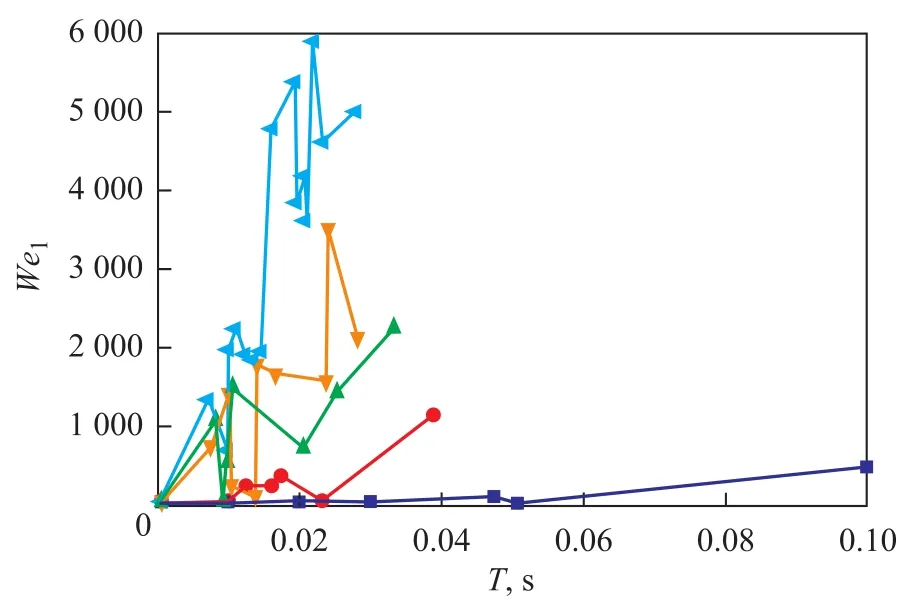
Figure 6 Effects of rotational speed on Weber number

4.2 Effect of rotational speed on droplets size

2.2.1 宣传教育不够，缺乏对秸秆综合利用方式的认识 由于农民传统的秸秆处理根深蒂固，加上受教育程度低使得对秸秆所拥有的经济价值和环境保护重要性的认识不足，从而对秸秆如何利用没有深入思考，不能从秸秆中的获得更多收入[4]。部分农户甚至对政府秸秆禁烧政策产生的抵触情绪，在夜间偷偷焚烧秸秆，焚烧所产生的二氧化碳、二氧化硫等气体，污染环境。

4.2.1 Selection of breakup model

Figure 7 shows the effect of rotational speed on the Weber number. When the rotational speed was about 300 r/min, only a small part of the Weber number of the droplets was greater than 100 (see Figure 7 (a)). However, when the rotational speed was more than 600 r/min, most of the Weber number of the droplets was greater than 100 (see Figure 7 (b), (c), (d), and (e)). Therefore, the TAB model was selected and the speed was specified at 300 r/min. The wave model was used when the speed was more than 600 r/min for subsequent calculations.

4.2.2 Effects of rotational speed on droplets diameter

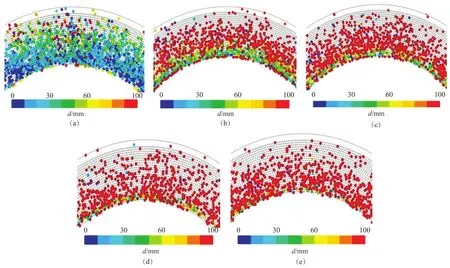
Figure 7 Effects of rotational speed on Weber number indicated by color chart (Q=400 L / h,=0.98 mm)

The effect of rotational speed on the diameter of the droplets is shown in Figure 8. The color of the distribution of droplets diameter became gradually dark as evinced by Figure 8 (a) to 8 (e), indicating that the droplets diameter increased when the rotational speed was increased from about 300 r/min to 1 200 r/min. Moreover, the result is similar to the effect of the rotational speed on the maximum diameter of the droplet, as shown in Figure 9 wherethe maximum diameter increased from 2.40 to 5.36 mm with an increasing rotational speed. This phenomenon occurred because the collisional Weber number (Wec) is a function of relative velocity, and the relative velocity increased between the droplets with an increasing rotational speed, thereby leading to their coalescence. Moreover, it can be seen from Figure 8 (a) to Figure 8 (e) that the number of droplets decreased when the rotational speed was increased from around 300 r/min to 1 200 r/min, showing that the droplets could readily grow together after collision. The effect of rotational speed on the minimum diameter of droplets is given in Figure 10. The droplet diameter sharply decreased from 0.05 mm to 9.6×10-6mm when the rotational speed was increased from 300 r/min to 600 r/min (see Figure 10(a)). This result illustrates that the gas phase flow has an important effect on the minimum diameter at a rotational speed of around 600 r/min, which is in agreement with the results referred to in the literature[16]. A study has shown[16]that the number of droplets on the packing surface significantly increased within the above range of the rotational speed, indicating indirectly that the droplets were broken in the above-mentioned range of rotational speed. Figure 10(b) is a partial enlargement of Figure 10 (a) in the rotational speed ranging from 600 r/min to 1 200 r/min. The minimum diameter continued to decreased sharply with an increasing speedW, and when the speed was 1 200 r/min, the minimum diameter was reduced to 1.28×10-6mm because the Weber number of the droplets was small (see Figure 6) at a rotational speed of 300 r/min, which indicates that the droplets surface was steady. However, the gas velocity can reach around 10 m/s[15]when the rotational speed was about 600 r/min, and the droplet surface gradually became unstable. At the same time, the turbulence of the gas phase flow on the droplets was also enhanced and thedroplets were broken into smaller pieces.

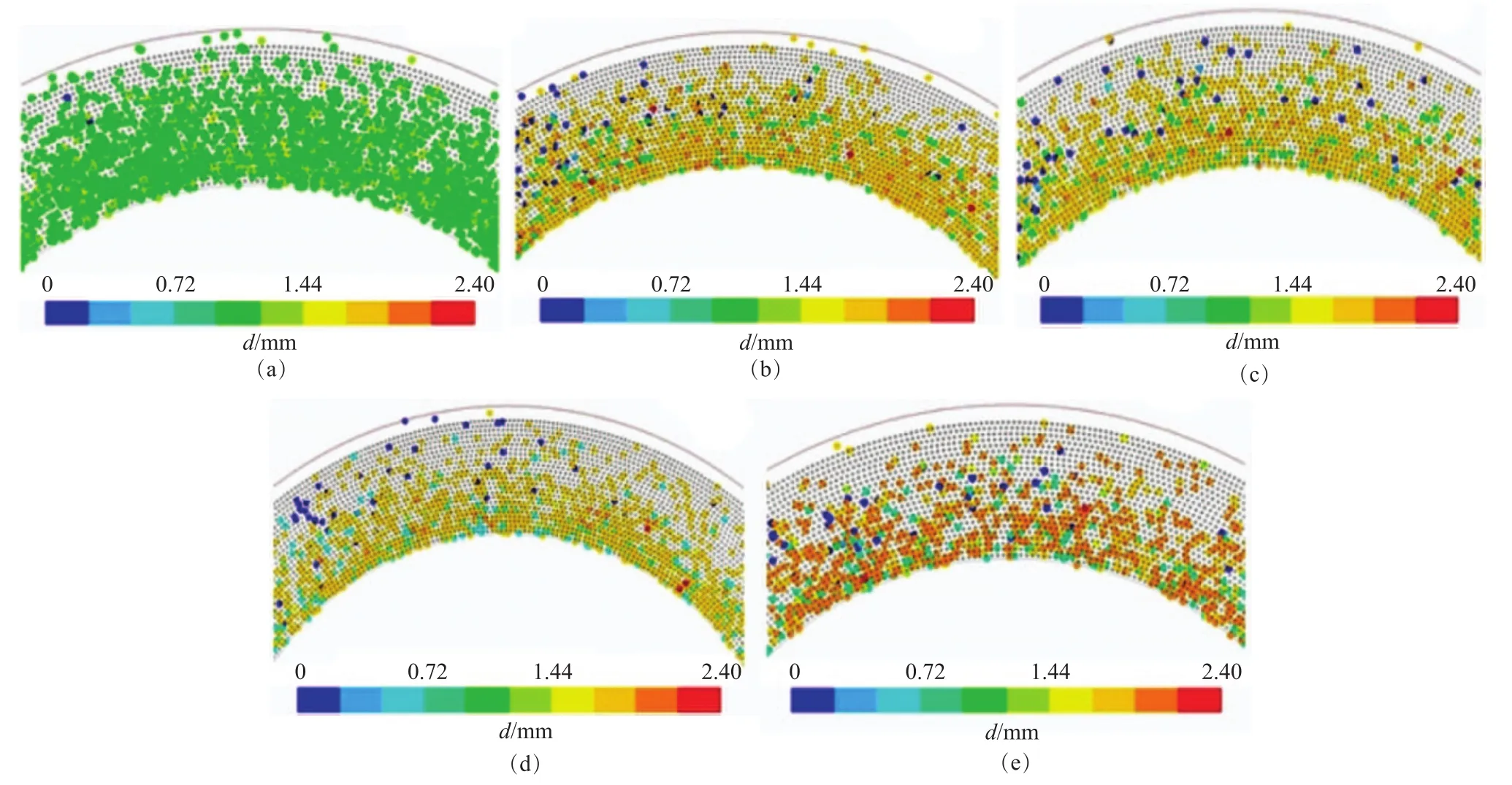
Figure 8 Effects of rotational speed on droplets diameter by color chart

Figure 9 Effects of rotational speed on maximum droplets diameter

Figure 10 Effects of rotational speed on minimum droplet diameter

4.2.3 Effects of rotational speed on distribution of droplets diameter

Upon tracking 200 droplets, the distribution of the droplets diameter at different rotational speeds is shown in Figure 11. Figure 12 displays the effect of rotational speed on the average diameter of droplets.

Figure 11 Effects of rotational speed on distribution of droplets diameter

In Figure 11, the number of droplets with their diameter being less than 0.98 mm increased with an increasing rotational speed. It can be seen from Figure 12 that the average diameter of the droplets still increased with an increasing rotational speed. This result indicates that the droplets tended to grow together inside the packing with an increasing rotational speed. Moreover, the CFD calculation error was 7.2% compared with the experimental values. This result might be caused by the following reasons: (1) The complete structure of RPB and fluid flow were simplified as a 2D model based on the restriction of computer performance; (2) The porosity of packing was reduced to approximately simulate the flow field, which could lead to smaller experimental values compared with the CFD value. To a definite extent, the CFD could reflect the effects of gas phase flow on the droplet diameter because the trends of the two ways of motion were similar to each other.

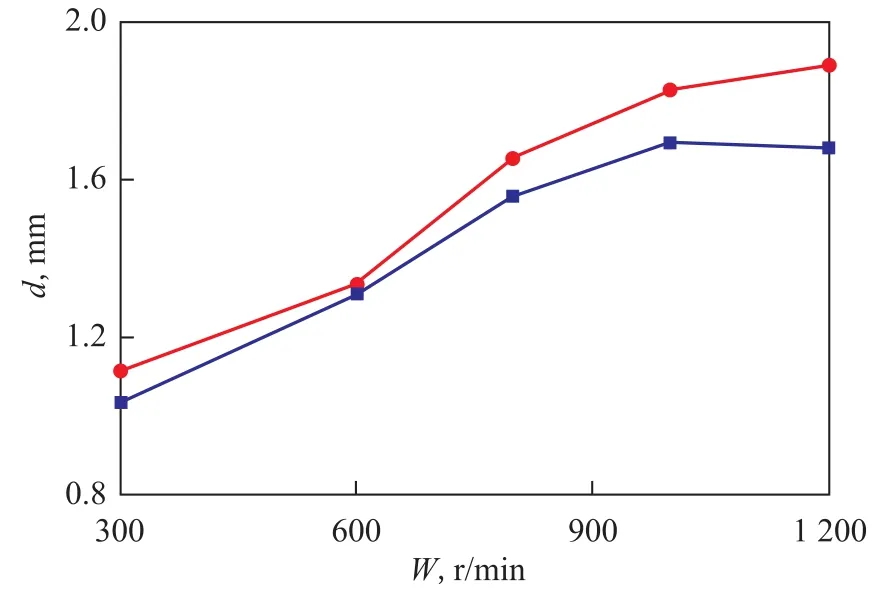
Figure 12 Effects of rotational speed on the droplets average diameter

5 Conclusions

The effect of gas phase flow on the droplet diameter inside the packing was simulated by CFD. The results were as follows:

(1) The Weber number of the droplets increased along the radial direction, and its value increased with an increasing rotational speed.

(2) The gas phase flow had an effect on the coalescence and breakup of the droplets inside the packing, which could be intensified with an increasing rotational speed. (3) The droplets tended to grow together inside the pack-ing because of the gas phase flow field, and the average diameter of droplets increased with an increasing rotational speed.

Acknowledgements:This work was financially supported by the Natural Science Foundations of China (No. 21206153, 21376229), the Excellent Youth Science and Technology Foundation of Province Shanxi of China (No. 2014021007), the Natural Science Foundation of Shanxi Province (Grant No.2011021012, 2012011008-2), and the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi (201316).

Nomenclature

d——Diameter, mm

r——Undisturbed droplet radius, mm

K——Ratio of total energy in distortion and oscillation energy (dimensionless)

Oh——Ohnesorge number (dimensionless)

t——Droplet movement time, s

Δt——Time step, s

Ta——Taylor number, dimensionless

W——Rotating speed, r/min

x——Displacement of the droplet equator from its spherical position, mm

Greek symbols

σ——Droplet surface tension, N/m

Ω——Maximum growth rate (dimensionless)

Λ——Wavelength, m

τ——Breakup time, s

Φ——Diameter of packing, m

[1] Zhang Xiaojun, Cheng Yun, Nie Songlin, et al. Simulation of multiphase flow of the oil-water separation in a rotating packed bed for oil purification[J]. Mathematical Problems in Engineering, 2013, 404327. http://dx.doi. org/10.1155/2013/404327

[2] Jiao W Z, Liu Y Z, Shao F, et al. Degradation of Wastewater Containing Nitrobenzene by High Gravity-Ultrasonic/ Ozonation/Electrolysis Technology[J]. China Petroleum Processing and Petrochemical Technology, 2012, 14(3): 96-101

[3] Jiao W Z, Liu Y Z, Liu W L, et al. Degradation of Nitrobenzene-Containing Wastewater with O3and H2O2by High Gravity Technology[J]. China Petroleum Processing and Petrochemical Technology, 2013, 15(1): 85-94.

[4] Qi Guisheng, Liu Youzhi, Pan Hongxia, et al. Hydrogen Sulfide Removal by Wet Oxidation Method in a Cross-Flow Rotating Packed Bed[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2012, 28(2): 195-199 (in Chinese)

[5] Yu Yong, Liu Youzhi, Qi Guisheng, et al. Selective removal of H2S from acid gas with chelated iron method in a rotating packed bed[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2014, 30(1): 60-65 (in Chinese)

[6] Qian Zheng, Zhang Haibing, Yan Guizhen. Comparison of rotating-packed bed and stirred bubbling tank reactor processes for high-TBN calcium petroleum sulfonate detergent preparation[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2009, 25(6): 861-867 (in Chinese)

[7] Lai Shuihong, Cai Xukui, Xu Zhichao, et al. The application of zigzag rotating bed in distillation apparatus[J]. Petro & Chemical Equipment, 2008, 11(5): 40-43 (in Chinese)

[8] Jiao Weizhou, Liu Youzhi, Shang Guanmin, et al. Dispersity characteristics of methanol-diesel oil emulsified fuel[J]. Journal of Fuel Chemistry and Technology, 2011, 39 (4):311-314.

[9] Liu Y Z, Jiao W Z, Qi G S. Preparation and properties of methanol-diesel oil emulsified fuel under high-gravity environment[J]. Renewable Energy, 2011, 36(5): 1463-1468.

[10] Jiao Weizhou, Liu Youzhi, Qi Guisheng. Rheological characteristics of diesel-methanol-water emulsions[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2010, 26(2): 214-218 (in Chinese)

[11] Jiao Weizhou, Liu Youzhi, Qi Guisheng. Physicochemical properties of the emulsions made from diesel, methanol and emulsifier[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2011, 27(1): 91-94 (in Chinese)

[12] Jiao Weizhou, Liu Youzhi, Qi Guisheng, et al. Pseudoternary diagrams of methanol-diesel emulsion[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2012, 28(1): 65-68 (in Chinese)

[13] Feng Guolin, Liu Youzhi, Jiao Weizhou, et al. Preparation and property of paraffin wax emulsion[J]. China Surfactant Detergent & Cosmetics, 2012, 41(6): 415-418 (in Chinese)

[14] Guan Xiaoming, Zhang Pengyuan, Chen Jianfeng. Preparation of Liquid Sulfonate Used in Enhanced Oil Recovery by Liquid Phase Sulfonation[J]. Journal of Chemical Engineering of Chinese Universities, 2010, 24(2): 296-300 (in Chinese)

[15] Shi Xing, Xiang Yang, Wen Lixiong, et al. Analysis of flow field for rotating packed bed based on the discrete phase model[J]. Journal of Chemical Engineering of Chinese Universities, 2012, 26(3): 388-394 (in Chinese)

[16] Zhang Jun, Guo Kai, Guo Fen, et al. Experimental study about flow of liquid in rotating packed bed[J]. Journal of Chemical Engineering of Chinese Universities, 2000, 14(4): 378-381 (in Chinese)

[17] Zhao Qinghua, Jing Xuejun, Chen Zhiliang, et al. Mass transfer characteristics and mechanism in a water-sparged aerocyclone[J]. CIESC Journal, 2013, 64(10): 3652-3657 (in Chinese)

[18] Yu H F, Li X G, Sui H, et al. CFD simulation of orifice flow in orifice-type liquid distributor[J]. China Petroleum Processing and Petrochemical Technology, 2013, 15(3): 70-78.

[19] Zhou X F, Yang Y Y, Wang G Q, et al. Estimating the operation status of steam cracking furnace using numerical simulation with combustion models[J]. China Petroleum Processing and Petrochemical Technology, 2012, 14(4): 52-63

[20] Dai Y Q, Liu W W, Wang S M, et al. HYSYS automation and its application on evaluation of plate heat exchanger[J]. China Petroleum Processing and Petrochemical Technology, 2008 (3): 55-59

[21] Llerena-Chavez H, Larachi F. Analysis of flow in rotating packed beds via CFD simulations—Dry pressure drop and gas flow maldistribution[J]. Chemical Engineering Science, 2009, 64(9): 2113-2126.

[22] O’Rourke P J. Collective Drop Effects on Vaporizing Liquid Sprays[D]. Princeton: Princeton University, 1981

[23] Taylor G I. The shape and acceleration of a drop in a high speed air stream[J]. The Scientific Papers of GI Taylor, 1963(3): 457-464

[24] Reitz R D, Bracco F V. Mechanisms of breakup of round liquid jets[J]. Encyclopedia of Fluid Mechanics, 1986(3): 233-249

[25] Reitz R D. Modeling atomization processes in high-pressure vaporizing sprays[J]. Atomization Spray Technology, 1987(3): 309-337

[26] Shi X, Xiang Y, Wen L X, et al. CFD analysis of liquid phase flow in a rotating packed bed reactor[J]. Chemical Engineering Journal, 2013, 228: 1040-1049

Received date: 2014-03-10; Accepted date: 2014-09-24.

Dr. Jiao Weizhou, Telephone: +86-351-3921986; E-mail: jwz0306@126.com.