A Method for Crude Oil Selection and Blending Optimization Based on Improved Cuckoo Search Algorithm

Yang Huihua; Ma Wei; Zhang Xiaofeng; Li Hu; Tian Songbai

(1. Guangxi Experiment Center of Information Science, Guilin University of Electronic Technology, Guilin 541004;2.Research Institute of Petroleum Processing, SINOPEC, Beijing 100083)

A Method for Crude Oil Selection and Blending Optimization Based on Improved Cuckoo Search Algorithm

Yang Huihua1; Ma Wei1; Zhang Xiaofeng1; Li Hu2; Tian Songbai2

(1. Guangxi Experiment Center of Information Science, Guilin University of Electronic Technology, Guilin 541004;2.Research Institute of Petroleum Processing, SINOPEC, Beijing 100083)

Refineries often need to find similar crude oil to replace the scarce crude oil for stabilizing the feedstock property. We introduced the method for calculation of crude blended properties firstly, and then created a crude oil selection and blending optimization model based on the data of crude oil property. The model is a mixed-integer nonlinear programming (MINLP) with constraints, and the target is to maximize the similarity between the blended crude oil and the objective crude oil. Furthermore, the model takes into account the selection of crude oils and their blending ratios simultaneously, and transforms the problem of looking for similar crude oil into the crude oil selection and blending optimization problem. We applied the Improved Cuckoo Search (ICS) algorithm to solving the model. Through the simulations, ICS was compared with the genetic algorithm, the particle swarm optimization algorithm and the CPLEX solver. The results show that ICS has very good optimization efficiency. The blending solution can provide a reference for refineries to find the similar crude oil. And the method proposed can also give some references to selection and blending optimization of other materials.

crude oil similarity; crude oil selection; blending optimization; mixed-integer nonlinear programming; Cuckoo Search algorithm

1 Introduction

In order to cope with the changes in the variety, quantity and price of crude oils, refineries often need to find alternative crude oil which is similar to the scarce crude oil. And the crude properties should be considered firstly when selecting the substitutes. However, even crude oils coming from the same field may have different properties, and then it is very difficult to find alternative crude oil with similar properties. Thus, using the similar blended crude oil to replace scarce crude oil will be a good approach. The physical process of blending the crude oils is simple, but the selection of proper crude oils and the determination of proper blending ratios are difficult[1].

Some crude oil properties cannot be calculated by linear addition method, which brings certain difficulty in predicting the blended crude properties. In the last few decades, many empirical equations have been proposed to calculate the blended crude properties[2-3]. And all these approaches provide theoretical support for crude oil blending, and comparatively few studies have been done on the blending optimization of crude oil. Ganji[3]applied SQP method for calculating the optimum blending ratios. Bai[4]proposed a two-level optimization structure, and applied a hybrid algorithm with Tabu search and differential evolution to the determination of blending sequence and corresponding flow rates. Du[5]considered the crude oil storage, transportation and blended properties simultaneously, and applied the genetic algorithm (GA) to identification of the blending ratios. Wang[6]applied the improved particle swarm optimization (PSO) algorithm to the multi-component naphtha recipe optimization problem, which could give some references to the crude oil blending optimization. Muteki[7-8]built a PLS model, and solved it by branch and bound algorithm to determine the selection of crude oils and their blending ratios simultaneously. However, there are some drawbacks in all above methods, they either ignore the opti-mization of crude oil selection or just build the model based on historical data which need a lot of pre-work to do.

The Cuckoo search (CS) was developed as a metaheuristic search algorithm by Yang and Deb in 2009[9]. It has less parameters to be fine-tuned, is very easy to realize programming, and works well on optimization problems in many fields[10-15]. However, no technical literature has been proposing on using CS in the crude oil selection and blending optimization problem up to now. We applied the improved CS (ICS) algorithm to solve the crude oil selection and blending optimization model, and the blending solution can provide a reference for refineries to find alternative crude oil.

2 Crude Oil Selection and Blending Optimization Model

2.1 Crude oil similarity

There are many methods for measuring the similarity between different individuals, such as inner product, cosine, correlation coefficient, and Dice coefficient, etc. Mc-Gill[16]gave 67 methods for different cases. On the other hand, many new similarity measuring methods are being proposed with an increasing demand for new applications. It is very important to select a suitable method for measuring the similarity. Here, we apply the method based on distance to measure the similarity between different crude oils, which is described in Equation (1).

We assume that the two crude oils arethe properties of which arerespectively. Then, the weighted similarity betweenis defined as follows:

2.2 Blended properties calculation

The crude oil properties can be divided into two categories as linear additivity and nonlinear additivity according to the relationship between the blended properties and raw material properties. For the linear additivity, some properties have additivity of mass, such as sulfur content, total acid number, and Conradson carbon residue, and others have additivity of volume, such as density, speci fic gravity, and refractive index parameter, etc.[2]On the other hand, the nonlinear properties include viscosity, pour point, smoke point, etc.

We assume thatPmixis the blended property,Piis the property ofithcrude oil, andRiis the mass fraction of theithselected crude oil.

With respect to the properties of mass additivity, we can use Equation (2) to calculatePmix,

With respect to the properties of volume additivity, we use Equation (3) to calculatePmix. And we consider the properties of volume additivity as nonlinear in this case.

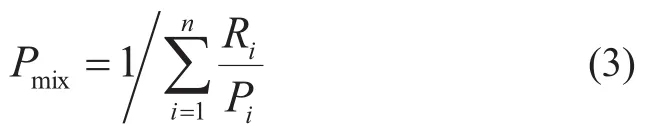
As for the nonlinear properties such as viscosity, pour point, and flash point, a lot of literature information have proposed experiential methods to predict the blended properties. In this paper, we use the method proposed in the literature[2],

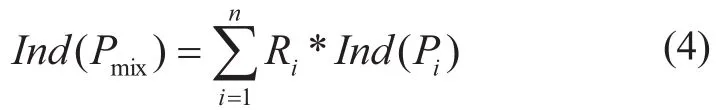
in whichIndis the index of properties and some of them are summarized in Table 1.

Table 1 Property indices for linearization

2.3 Blending optimization model

We assume thatX(N,M) is the property matrix of the available crude oils (in whichNis the number of available crude oils, andMis the number of properties).X(n,m) is the property matrix of selected crude oils (inwhichnis the number of selected crude oils, andmis the number of measured properties). The mass fraction of crude oils used in the crude blend isR=(R1,R2, …,Rn).

Oobjis the objective crude oil, andOmixis the blended crude oil. Then, the crude oil selection and blending optimization model is described as follows:

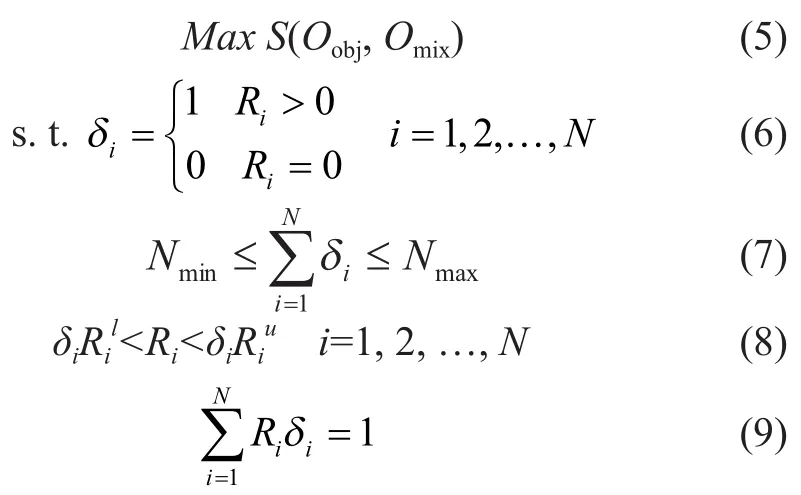
Equation (5) is the objective function, and its objective is to maximize the similarity between the blended crude oil and the objective crude oil. The calculation method of similarity is Equation (1), and the blended properties are calculated by Equation (2) through Equation (4).

Equations (6) and (7) are the constraints of binary decision variables. Hereδiwill be set as 1 if the crude oil is selected, or otherwise will be set as 0.NmaxandNminare the upper and lower limit of the number for selected crude oils, respectively.

Equations (8) and (9) are the constraints of decision variableare respectively the upper and lower limit of blending ratios for the selected crude oils. Furthermore, the total ratio ofRimust be 1.

In general, the model is a mixed-integer nonlinear programming with constraints. And it belongs to the class of NP-hard optimization problems, which cannot be solved efficiently by any known algorithm in a practically acceptable time scale. In the most cases, we can use metaheuristic search algorithm to get proximate optimum solution. On the other hand, only the decision variableRis left when the available crude oil numberNis equal to both the upper limitNmaxand the lower limitNmin(which meansNmax=Nmin=N), and then, the problem will be transformed into the blending ratios optimization only, and this belongs to a nonlinear continuous optimization problem which is easier to solve.

3 Improved Cuckoo Search Algorithm

Basic CS algorithm is very effective in solving continuous optimization, but has no capacity to solve the problem with mixed-integer variables. Thus, for establishing the crude oil selection and blending optimization model, we have improved the encoding scheme and the Lévy flights in order to deal with the 0-1 mixed-integer problems. The main idea of ICS is described as follows: 1) A real-coded scheme is proposed, which takes into account the binary variablesδand the continuous variableR. And this measure can avoid the complex operation with binary variables; 2) The continuous variables by Lévy flights are updated, while keeping the binary variables constant; 3) The binary variables are updated by abandoning nests with a probability.

3.1 Encoding scheme

The encoding scheme proposed hereby considers the fractionRand the binary variableδsimultaneously. And it also takes into account the constraints (7) and (9). Each scheme represents one feasible solution. Upon taking ten available crude oils as an example, we can suppose that the crude oil number isX01,X02, …,X10. Then, the encoding process is expressed as follows:

Step 1: Ten stochastic real numbers in the range of 0 to 1 are generated:

Step 2: A stochastic integerNfromNmintoNmaxis selected, which is seen as the number of selected crude oils in this encoding scheme. (Here, we assume that theNis 4).

Step 3:Nvariables are randomly selected from the variables generated by Step 1, and would remain unchanged, meanwhile, other variables are set as 0: (0.401 3, 0.555 7, 0, 0, 0.699 4, 0, 0, 0, 0.62 9 1, 0);

Step 4: Normalize the individual which is generated by Step 3. Then, we can get the final encoding scheme: (0.175 6, 0.243 1, 0, 0, 0.306 0, 0, 0, 0, 0.275 3, 0).

The encoding scheme mentioned above represents a blending solution, namely, blending theX01,X02,X05 andX09 crude oils with a mass percentage of 17.56%, 24.31%, 30.60% and 27.53%, respectively.

3.2 Lévy flights

The following Equation (10) is applied to update the location for a Cuckooi, by a Lévy flights:

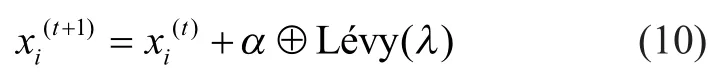
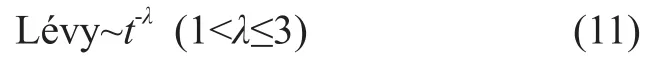
which has an infinite variance with an infinite mean.

In the CS algorithm, Yang[9]applied the method proposed in the literature[17]to calculate the step length:

wheresis the step length andβis set as 1.5.uandvare drawn from normal distribution:

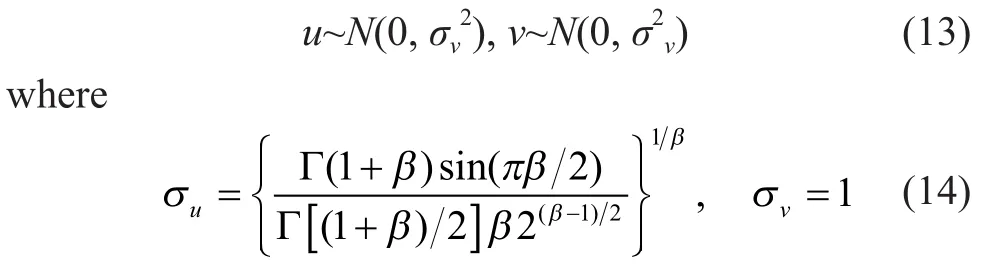
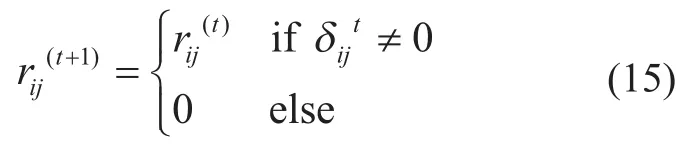
Finally, we normalize the individual to keep the total ratio to be 1. And then it is necessary to validate the individual, or replace it by a new one if it is infeasible.

3.3 Algorithm process

We assume that each nest contains only one egg. Based on the improved encoding scheme and the Lévy flights, the steps of ICS can be summarized as follows:

Step 1: Initialize the algorithm parameters: the nest numbern, the discover probabilityPa∈(,)0 1, and the maximum generationIter;

Step 2: Generate initial population ofnhost nestsxi(i=1, 2, …,n) according to the encoding scheme proposed by Section 3.1;

Step 3: Evaluate the fitness of each nest according to the similarity. Find the best nestxbest;

Step 4: Update the position ofxithrough Lévy flights; and keep the best one;

Step 5: Validate each nest, and, if infeasible, replace it by a new nest;

Step 6: Abandon a fraction (Pa) of worse nests, and then set up new ones;

Step 7: Find the best nestxbestfrom the nests generated by Steps 4 and 6;

Step 8: Go to Step 9 if the maximum generation is reached, otherwise, go to Step 4 for the next iteration;

Step 9: Harvest the best result (blending solution and the similarity).

4 Experiments and Discussion

In order to validate the proposed approach, the results of ICS are compared with GA[18], PSO[19]algorithm and CPLEX[20]solver. The encoding scheme and the handling method of constraints for both GA and PSO are the same with ICS.

4.1 Experiment data

We have carried out four experiments, and the four sets of crude oil property data are obtained from the crude oil database of the SINOPEC Research Institute of Petroleum Processing (RIPP), independently.

Experiment 1: The property matrixX(10, 7) consists of measurements of 7 properties from 10 varieties of crude oils. And the properties consist of sulfur content (SUL), nitrogen content (N), total acid number (TAN), Conradson carbon residue (CCR), asphaltenes content (APH), nickel content (Ni) and vanadium content (V). The calculation of these blended properties is conducted according to Equation (2).

Experiment 2: Increase the crude oil varieties to 50 based on Experiment 1, and the property matrix isX(50, 7).

Experiment 3: Add another three nonlinear properties based on Experiment 1. And the properties are comprised of density@20 ℃ (D20), viscosity@20 ℃ (V20), and pour point (PP). Hence, the property matrix isX(10, 10).

Experiment 4: Increase the crude oil varieties to 50 based on Experiment 3, and the property matrix isX(50, 10).

The property data of Experiments 1 and 3 are listed in Table 2.

4.2 Results and discussion

The simulation was implemented using Matlab R2009aunder the 64 bit Win7 operating system. Experiments were conducted on a laptop equipped with Intel CoreTMi3 Duo 2.53 GHz, and 4 GB of RAM.

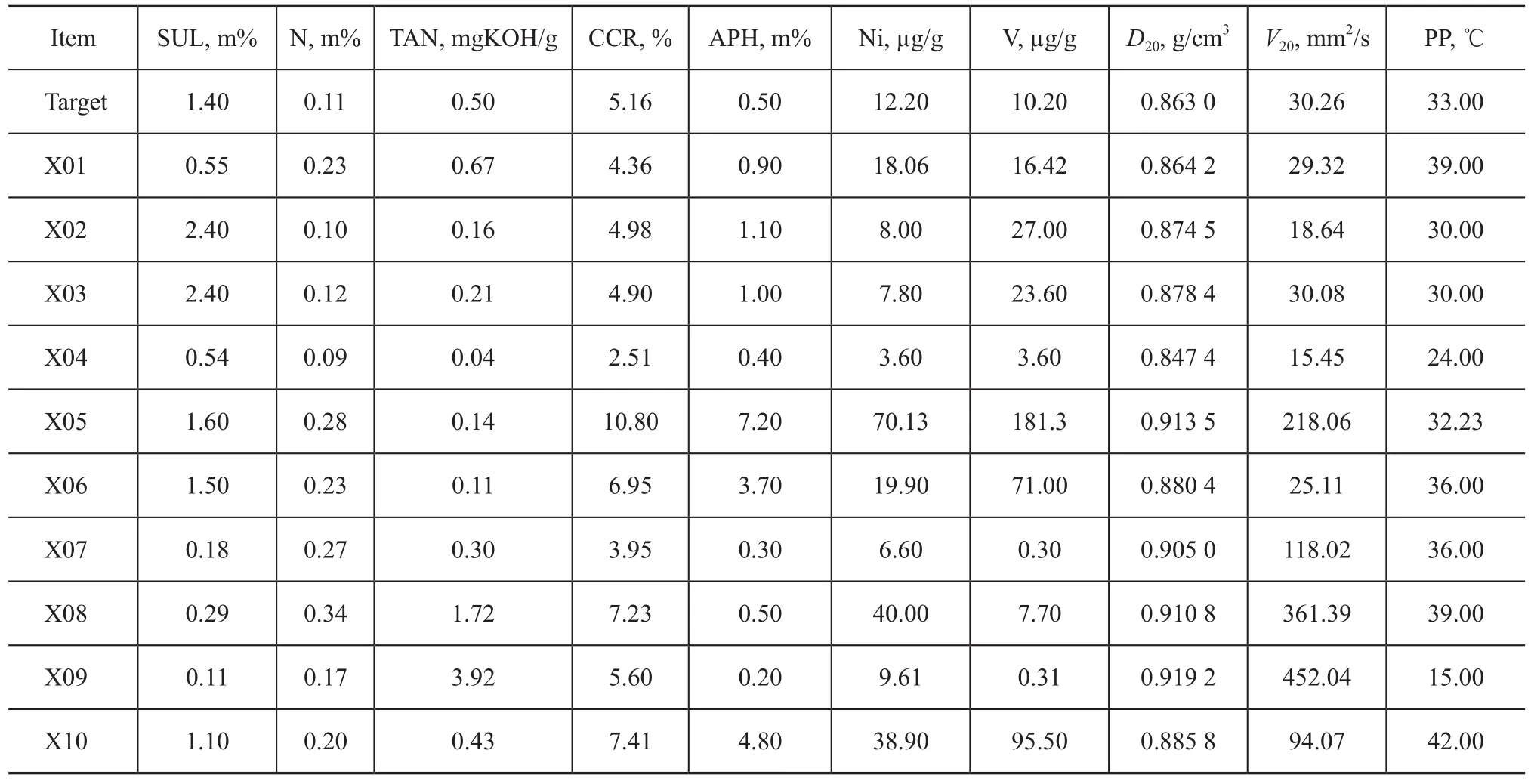
Table 2 The property data of crude oil for Experiments 1 and 3

The parameters used in all our experiments for each algorithm are shown in Table 3:

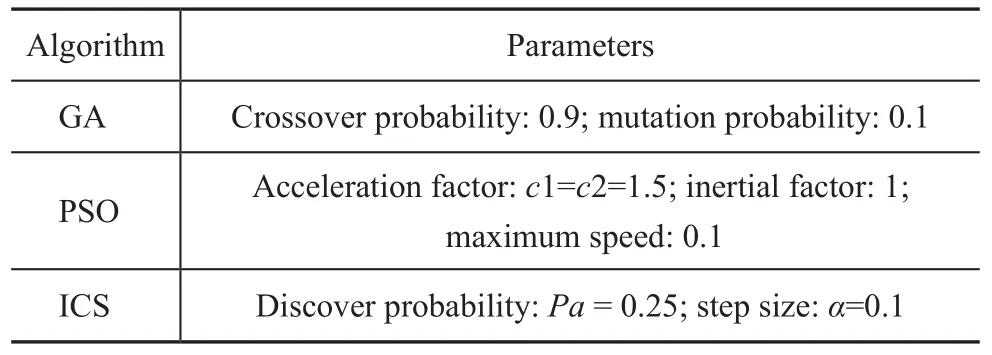
Table 3 Parameter setting for each algorithm

In each experiment, we set the constrained variablesNmin,respectively. In most cases, refineries can set the weight for each property according to their experience. Here, we set all the weights equally for the sake of simplicity.

For each algorithm, the population numbernand the maximum generationIterare set as 50 and 500 for both Experiment 1 and Experiment 3, and 200 and 1000 for both Experiment 2 and Experiment 4, respectively.

With the parameters setting above, each algorithm was run 100 times independently, and the final results are shown in Tables 4 through 11, and Figures 1 through 2.

Table 4 Blending solution for Experiment 1

Table 5 Final blended properties applicable to Experiment 1

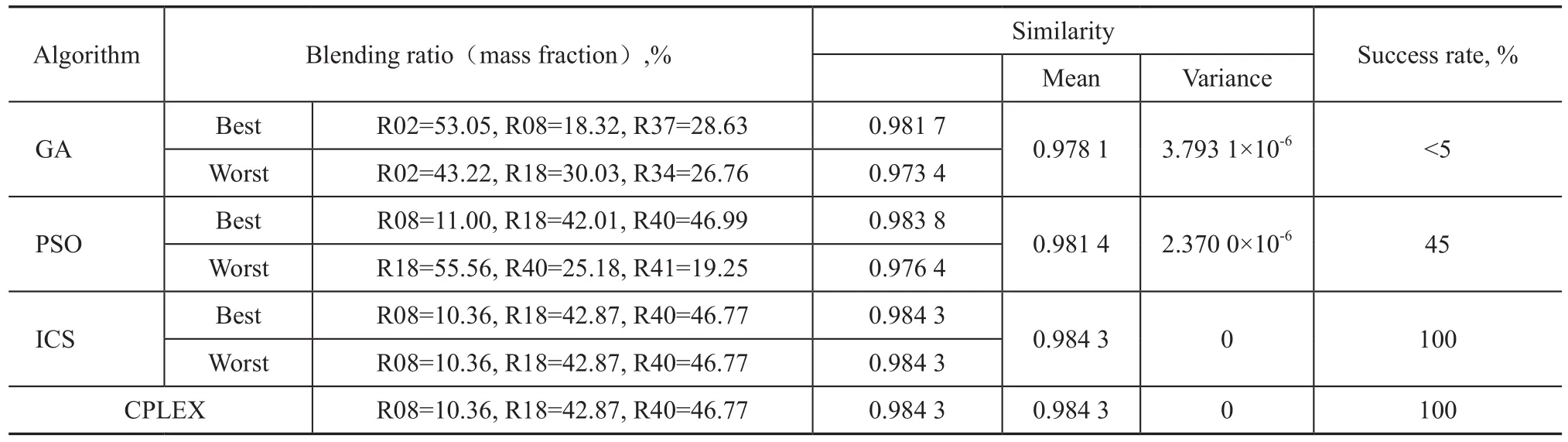
Table 6 Blending solution for Experiment 2

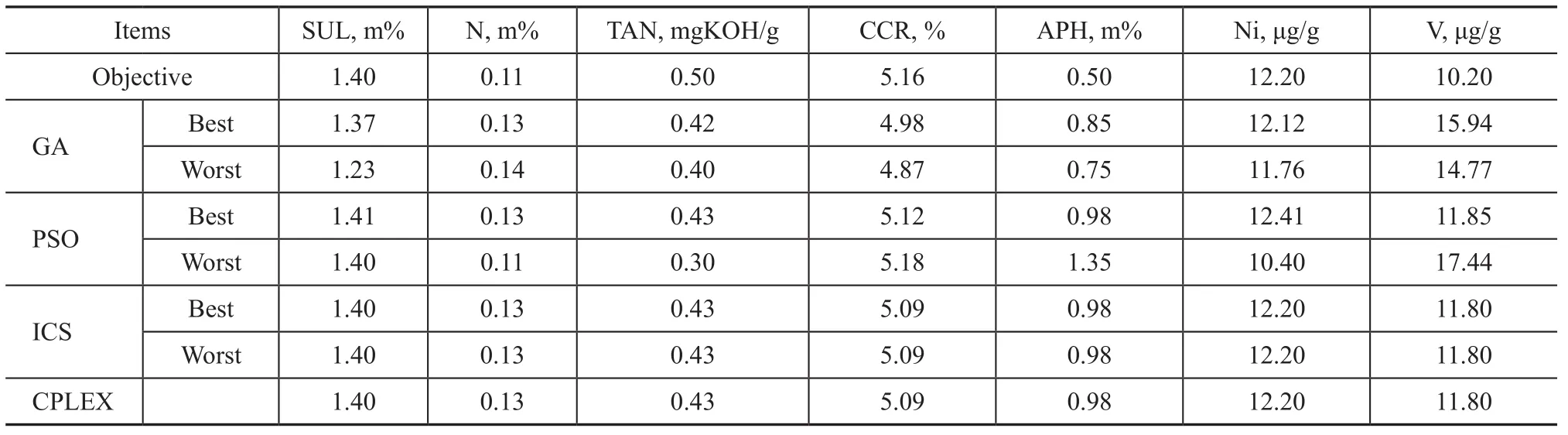
Table 7 Final blended properties applicable to Experiment 2

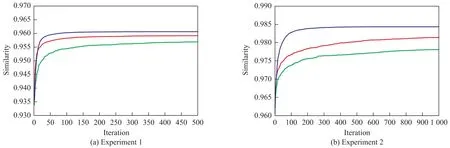
Figure 1 Curve of evolution optimization (average of 100 runs)

Tables 4 and 5 show the results of Experiment 1. The row‘Best’ shows the best solution found by each algorithm, and the row ‘Worst’ gives the worst solution. Furthermore, the column ‘Mean’ and ‘Variance’ show the average and variance of similarity respectively for the 100 independent runs of each algorithm. We can see that the result of ICS is consistent with that of CPLEX after 500 iterations, and its success rate reaches a high level with 98% of coincidence. By contrast, although the best result of both GA and PSO are consistent with CPLEX too, their success rates are much lower than ICS. Compared with the mean and the variance of similarity, we can see that ICS has much higher robustness than both GA and PSO.

Table 6 and 7 show the results of Experiment 2. It is clear that GA cannot get a stable result after 1 000 iterations. And the result of PSO is similar with that achieved in Experiment 1, but the success rate decreased from 52% to 45%. By contrast, both the best and the worst results of ICS are consistent with CPLEX, and the success rate reaches 100%. This experiment illustrates that ICS also has a very good optimization efficiency even the available crude oil varieties increase to 50.

Figure 1 is the curve of evolutionary process for Experiments 1 and 2. Upon taking the average similarity of each algorithm as their convergence boundary independently, we have found out that the convergent generations of GA, PSO and ICS are 457, 268 and 205, respectively, for Experiment 1, and are 918, 918 and 394 for Experiment 2. The evolutionary process indicates that the convergent effect with ICS is much better than both of GA and PSO.

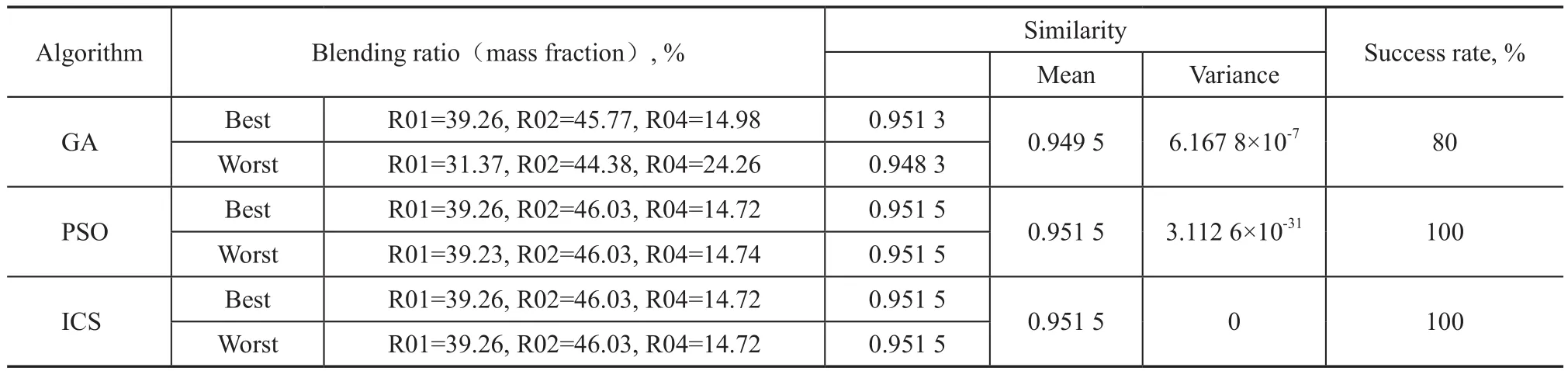
Table 8 Blending solution for Experiment 3

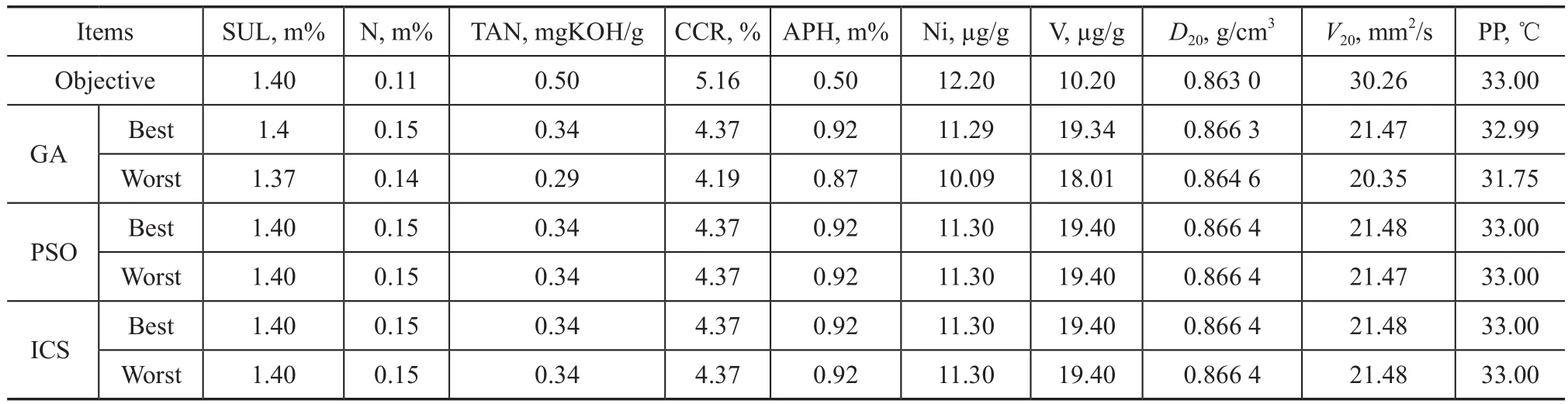
Table 9 Final blended properties applicable to Experiment 3

Table 10 Blending solution for Experiment 4

Table 11 Final blended properties applicable to Experiment 4

Figure 2 Curve of evolution optimization (average of 100 runs)

Nonlinear nature will be brought into the decision expression of CPLEX while nonlinear properties are added into the model. However, CPLEX could not solve the model in this case. Thus, we just compare ICS with GA and PSO on the results of Experiments 3 and 4.

Tables 8 and 9 show the results of Experiment 3. It can be seen that the best result of each algorithm is consistent. The high success rates indicate that each algorithm has very good optimization effect. Furthermore, the success rates of GA, PSO and ICS are 80%, 100% and 100, respectively, which shows that both PSO and ICS have higher robustness than GA. On the other hand, the convergent generations of PSO and ICS are 254 and 37, respectively, in Figure 2(a), which shows that ICS has a faster convergence speed.

Tables 10 and 11 show the results of Experiment 4. In this case, GA is almost impossible to get a stable solution. The success rates of PSO and ICS are 65% and 92%, respectively, which shows that ICS has a higher robustness than PSO. On the other hand, the blending solution of ICS is better than PSO in terms of the similarity. Figure 2(b) shows that ICS is almost convergent, and both GA and PSO are not convergent after 1000 iterations, and this result is similar with Experiment 2. Moreover, the success rate of GA, PSO and ICS decreased from 80%, 100% and 100% to less than 5%, 65% and 92%, respectively. This experiment indicates that the robustness of both GA and PSO are greatly affected by the increase of available crude oil varieties, and by contrast, ICS has a more strong robustness.

Moreover, the method could give several different solutions with high similarity. For example, although the best and the worst blending solution got by ICS in Experiment 4 are different, the similarity and blended properties are close. And refineries could select suitable blending solution while taking into account other factors such as the material supply.

5 Conclusions

We have built a mixed-integer nonlinear programming (MINLP) model based on the data of crude oil property, with the objective of maximizing the similarity between the blended crude oil and the objective crude oil. Themodel can transform the problem of looking for similar crude oil into the crude oil selection and blending optimization. The improved CS algorithm is discretized and then used to solve the model. This method can determine the selection of crude oils and their blending ratios simultaneously. Compared with GA and PSO, ICS has a better result and a higher convergent rate in solving such problems. Moreover, ICS algorithm has less parameter to be fine-tuned and is very easily applied to perform programming. Refineries can select the available crude oils, measure their properties and set the weight for each property flexibly based on the crude oil database. The result can provide a reference for looking for alternative crude oils. Furthermore, the proposed method can also provide a reference for blending optimization of other materials.

Acknowledgements:This paper has been partly supported by the National Natural Science Foundation of China (No. 21365008), and the Science Foundation of Guangxi province of China(No. 2012GXNSFAA053230).

[1] Speight J G. The Chemistry and Technology of Petroleum[M]. CRC Press, 2010.

[2] Riazi M R. Characterization and Properties of Petroleum Fractions[M]. ASTM, 2005.

[3] Ganji H, Zahedi S, Marvast M A, et al. Determination of suitable feedstock for refineries utilizing LP and NLP models[J]. International Journal of Chemical Engineering and Applications, 2010, 1(3): 225-310.

[4] Bai L, Jiang Y H, Huang D X, et al. A novel scheduling strategy for crude oil blending[J]. Chinese Journal of Chemical Engineering, 2010, 18(5): 777-786.

[5] Du H K, Zhao Y K. Research of mixed optimization of crude oil based on genetic algorithms[J]. Control and Instruments in Chemical Industry, 2010, 37(1): 8-10 (in Chinese).

[6] Wang L N, Cao C W. Research on multi-component naphtha recipe optimization with improved particle swarm optimization using cultural algorithm[J]. Automation in Petrochemical Industry, 2012, 48(1): 43-47 (in Chinese).

[7] Muteki K, Macgregor J F, Ueda T. Mixture designs and models for the simultaneous selection of ingredients and their ratios[J]. Chemometrics and Intelligent Laboratory Systems, 2007, 86(1): 17-25.

[8] Muteki K, Macgregor J F, Ueda T. Rapid development of new polymer blends: the optimal selection of materials and blend ratios[J]. Industrial & Engineering Chemistry Research, 2006, 45(13): 4653-4660.

[9] Yang X S, Deb S. Cuckoo search via Lévy flights[C]// World Congress on Nature & Biologically Inspired Computing (NaBIC 2009, India). IEEE Publications (2009): 210-214.

[10] Yang X S, Deb S. Engineering optimisation by Cuckoo search[J]. International Journal of Mathematical Modeling and Numerical Optimisation, 2010, 1(4): 330-343.

[11] Yang X S, Deb S. Cuckoo search: Recent advances and applications[J]. Neural Computing and Applications, 2013, 24(1): 169-174.

[12] Yildiz A R. Cuckoo search algorithm for the selection of optimal machining parameters in milling operations[J]. The International Journal of Advanced Manufacturing Technology, 2013, 64(1/4): 55-61.

[13] Gherboudj A, Layeb A, Chikhi S. Solving 0-1 knapsack problems by a discrete binary version of Cuckoo search algorithm[J]. International Journal of Bio-Inspired Computation. 2012, 4(4): 229-236.

[14] Ouaarab A, Ahiod B I D, Yang X. Discrete Cuckoo search algorithm for the travelling salesman problem[J]. Neural Computing and Applications, 2013, 24(7/8): 1659-1669.

[15] Ouyang X, Zhou Y, Luo Q, et al. A novel discrete Cuckoo search algorithm for spherical traveling salesman problem[J]. Appl Math, 2013, 7(2): 777-784.

[16] McGill M, Koll M, Norreault T. An evaluation of factors affecting document ranking by information retrieval systems[R]. Syracuse University: School of Information Studies 1979.

[17] Mantegna R N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes[J]. Physical Review E, 1994, 49(5): 4677-4683.

[18] Holland J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66-72.

[19] Kennedy J, Eberhart R. Particle Swarm Optimization[M]. Encyclopedia of Machine Learning, Springer, 2010, 760-766.

[20] IBM ILOG CPLEX 12.6. http://www-01.ibm.com/software/commerce/optimization/cplex-optimizer /index.html.

Received date: 2014-02-25; Accepted date: 2014-09-24.

Professor Yang Huihua, E-mail: yang98@guet.edu.cn; Professor Tian Songbai, E-mail: tiansb. ripp@sinopec.com.