高速移动荷载作用对桥上轨道竖向动力特性的影响
陈 江,李成辉,黄家聪
(西南交通大学高速铁路线路工程教育部重点实验室,四川成都 610031)
近年来我国高速铁路迅速发展,新建并开通了总里程居于世界首位的无砟轨道[1],最高运营速度达到350 km/h。为延长车辆和线路使用寿命、保证列车行驶的平稳、舒适和安全性,深入研究高速列车与轨道结构相互作用及动力特性是非常重要的。
轨道结构与高速列车通过车轮与钢轨的接触相互作用产生的振动是加速设备破坏,影响行车平稳、舒适,甚至安全的主要因素。引起振动的原因主要有三方面:轮轨不平顺、轨下基础刚度不均匀和线路荷载的移动特性。
轮轨不平顺是指钢轨几何形位误差和钢轨工作面的伤损和缺陷[2],以及车轮不圆顺等[3]。轮轨系统不平顺是轮轨系统振动的主要激振源,国内外已有大量研究工作以轨道竖向不平顺作为激励源,建立列车—轨道—桥梁系统模型分析列车高速通过桥上轨道时列车、轨道结构和桥梁的振动特性[4-5]。轨下基础刚度不均匀是指轨下胶垫失效、扣件失效、过渡段问题等[6-8]。轨下基础刚度不均匀能引起车辆线路振动是因为车轮作用于钢轨的荷载是移动的。列车车轮荷载使钢轨产生竖向位移,形成一条以轮轨的接触点为中心的位移变形曲线,竖向位移的大小与轨下基础刚度有关。列车车轮通过轨下基础刚度不均匀地段时,轮下线路竖向位移是变化的,使车轮上下振动而引起轮轨系统振动,如过渡段问题等[9]。此外,轮下钢轨位移曲线还会随车辆前进而向前运动,形成了向前传播的轨道位移波。当列车速度接近于线路位移传递速度时,线路会引起剧烈的振动[10]。
类似于过渡段,当列车车轮通过桥上轨道时、车轮对应处轨下(桥台和梁跨不同部位)竖向刚度不一致,也会引起轮轨系统振动。而且这种振动主要是荷载移动特性引起的,即使没有不平顺也会产生。
关于桥梁在移动荷载作用下竖向位移的影响已有一些理论研究工作[11-13],主要建立移动荷载—简支梁模型,分析了高速移动荷载作用对桥梁竖向位移及动力特性的影响;但对于高速列车通过桥上无砟轨道时,荷载移动特性对桥上轨道的影响还有待研究。因此,本文以成灌铁路桥上无砟轨道结构为背景,建立移动荷载作用下简支梁桥上轨道结构力学模型,探讨高速移动荷载作用对桥梁上轨道竖向动力特性的影响。
1 力学模型
我国高速铁路无砟轨道线路桥梁以简支箱梁桥为主,桥梁上无砟轨道结构从上到下依次为钢轨、扣件、道床板、调整层、底座板等,如图1、图2所示。当列车通过桥梁时,轮下整体结构在竖向荷载作用下产生挠曲变形,因此可将桥梁和轨道简化为等效简支梁(参见图3)。等效简支梁的单位长度质量为轨道结构各部分和桥梁单位长度质量的总和,其等效抗弯刚度为轨道各部分抗弯刚度和桥梁抗弯刚度的总和。轨道桥梁等效单位长度质量可简单地将轨道各部分单位长度质量和桥梁单位长度质量相加得到,但轨道桥梁的等效抗弯刚度的计算还应考虑各层间结构的性能。

图1 桥上无砟轨道结构横截面
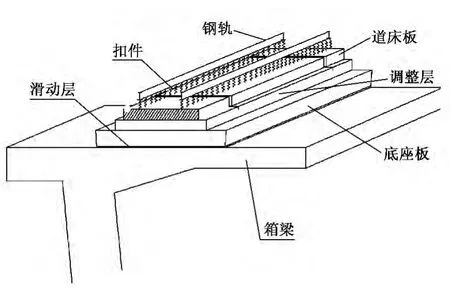
图2 桥上无砟轨道结构纵向示意
钢轨与道床板间通过扣件联结,设计要求钢轨不爬行,所以钢轨与轨枕(道床板)无纵向位移。道床板与底座板之间有调整层,并有凸台或其它定位装置约束,但其长度相对较小,因此在弯曲时层间是滑动的,从而可将钢轨和道床板考虑为整体,二者之间无相对层间滑动。底座板与箱梁之间铺设滑动层,层间可滑动,因此底座板可看作是独立作用的梁。这样将桥上无砟轨道在竖向上看成是桥梁、底座板与钢轨,以及道床板组成的三层叠合梁。其等效抗弯刚度为箱梁、底座板抗弯刚度及钢轨与道床板组合抗弯刚度之和。
根据简支梁边界条件、桥上无砟轨道等效单位长度质量和抗弯刚度得到移动荷载作用下桥上轨道动力分析模型,如图3所示。其中,W(x,t)为轨道桥梁的竖向位移。u为荷载移动速度,t为荷载移动时间,m为轨道桥梁的等效单位长度质量、EI为轨道桥梁的等效抗弯刚度、l为梁的长度,F为轴重。
2 系统动力响应方程
根据图3中的力学模型,假设梁上荷载F以匀速u向右运动,在t=0时,荷载F位于左边A处,t时刻荷载距A的距离为a=ut。梁上轨道结构的振动微分方程为

图3 桥上轨道移动荷载力学模型
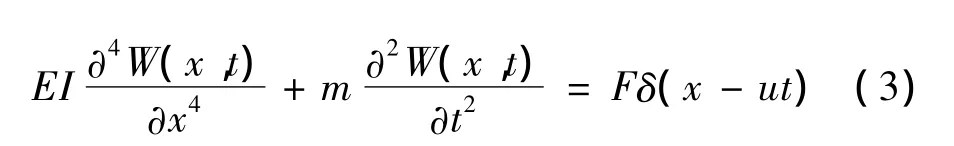
式(3),δ为Dirac函数。
本文利用振型叠加法求解。根据振动理论简支梁的振型函数为正弦函数[14]
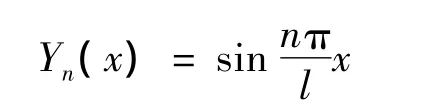
因此可得轨道桥梁的竖向位移
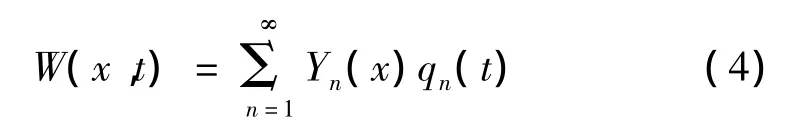
式中,qn(t)为振型坐标。
将式(4)代入式(3),根据初始条件为qn(0)=n(0)=0,整理后得到,轨道竖向位移为

求解竖向位移响应时,虽然求和上限为无穷项,但实际计算时可根据精度选取有限项。本文经计算,上限取100时,计算相邻两阶的计算误差已<1×10-6,因此在计算中取100阶做振型叠加。
3 计算结果及分析
3.1 计算参数
根据上述力学模型,以成灌铁路32 m简支梁桥及CRTSⅢ型板式无砟轨道结构为算例,根据其参数(如表1),可得轨道桥梁的等效抗弯刚度为2.43×108kN/m2,等效单位长度质量为24 052.5 kg/m。列车荷载取成灌铁路运营的CRH1动车组的单轮对最大轴重160 kN。
3.2 荷载作用点竖向位移
根据桥上轨道竖向位移响应方程解,编程分别计算了列车荷载以 150,200,250,300,350 km/h 5 种不同的速度通过桥上无砟轨道时,车轮作用处的轨道竖向位移响应,以及车轮静荷载在不同位置时作用点处竖向位移响应,如图4所示。
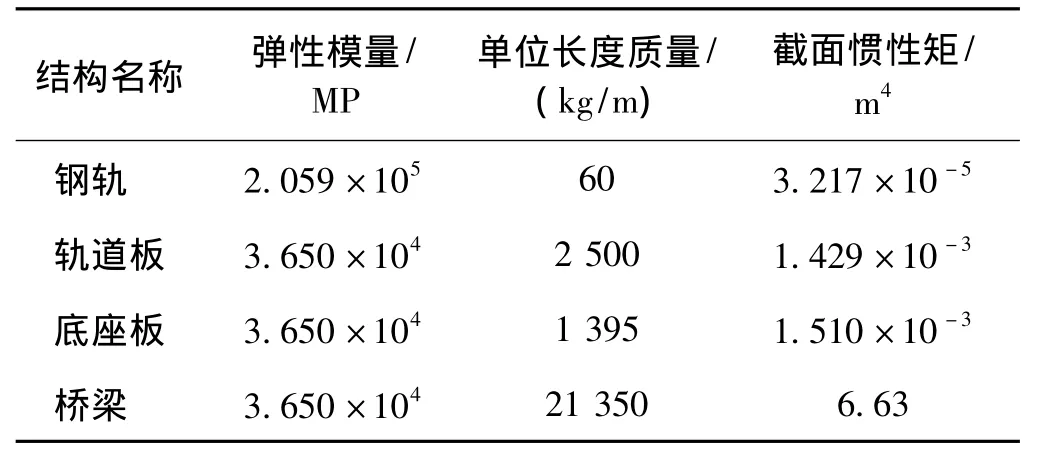
表1 成灌铁路轨道桥梁参数

图4 荷载作用处轨道竖向位移
根据图4中列车车轮荷载作用处轨道竖向位移计算结果可知,静荷载和速度为 150,200,250,300,350 km/h 5种工况下梁上荷载作用处轨道的最大竖向位移分别为 0.449,0.514,0.498,0.493,0.581,0.645 mm。350 km/h时轨道的最大竖向位移最大且为静荷载作用情况下最大竖向位移的1.44倍。速度为150 km/h时的最大竖向位移要大于速度为200 km/h和250 km/h时的最大竖向位移值,说明并非荷载移动速度越大,桥上轨道的竖向位移也越大。
图4中每种工况下桥上轨道竖向位移曲线显示,列车荷载高速通过简支梁桥上轨道时,在没有考虑轨道不平顺的情况下,桥上轨道结构也会引起竖向振动。荷载移动速度为150 km/h时,梁上轨道结构竖向位移变化相对缓慢,但位移曲线出现的振动次数较多,振幅相对较小。速度为350 km/h时,梁上荷载作用处的轨道结构竖向位移曲线波动较小,振幅较大。因此,桥上荷载作用处轨道结构的竖向位移振动频率与荷载移动速度有关,对二者的规律需做进一步的研究。
3.3 跨中位置竖向位移
根据上文已经推导出的桥上轨道竖向位移响应方程解,编程分别计算了列车荷载以150,200,250,300,350 km/h 5种不同的速度通过桥上无砟轨道时,桥上跨中位置轨道的竖向位移响应,以及车轮静荷载作用在不同位置时桥上跨中位置轨道结构的竖向位移响应,如图5所示。
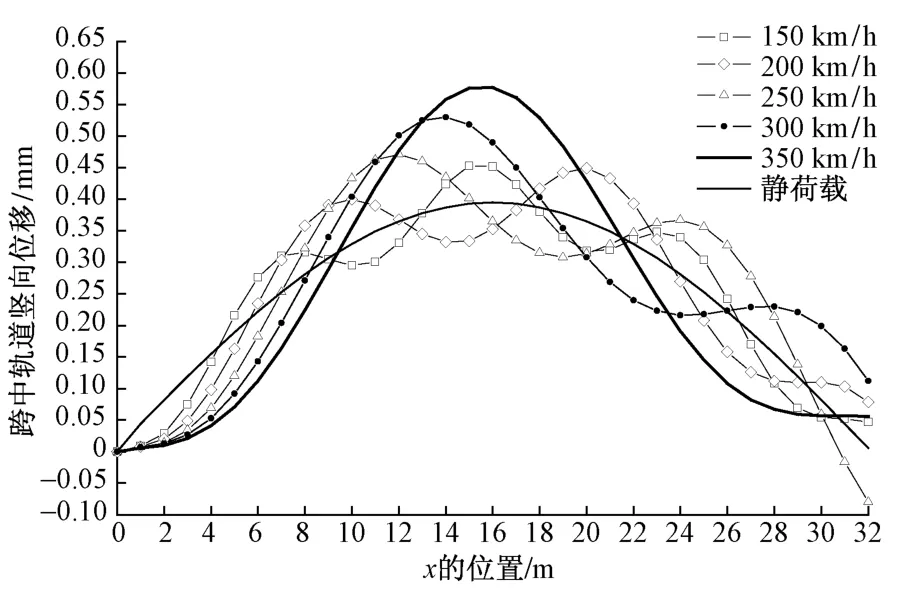
图5 移动荷载作用下桥上跨中轨道竖向位移
静荷载和速度为 150,200,250,300,350 km/h 6种工况下梁上荷载作用处轨道的最大竖向位移分别为 0.395,0.453,0.449,0.471,0.530,0.577 mm。荷载以250 km/h的速度,移动至桥梁末端时跨中处轨道的竖向位移方向向上。
在每种移动荷载工况下,由跨中位置轨道竖向位移曲线看出,跨中位置的轨道结构都产生了振动,且振动频率与速度相关。
3.4 桥上轨道最大竖向位移对比
在10~350 km/h之间每相隔10 km/h为一种工况,计算了桥上轨道结构的竖向位移最大值,以及静荷载工况下的桥上轨道结构最大竖向位移,计算结果如图6所示。

图6 不同速度下桥上轨道最大竖向位移
由图6可见:①移动荷载作用情况下桥上轨道结构最大竖向位移均大于静荷载工况下的最大竖向位移。静荷载作用下轨道最大竖向位移为0.449 mm,移动荷载速度为350 km/h时最大竖向位移为0.645 mm。②并非荷载移动速度越大桥上轨道最大竖向位移就越大。③当速度>210 km/h时,桥上轨道的最大竖向位移随速度的增加近似呈线性增长。
4 结语
1)在不考虑轨道不平顺影响时,高速移动荷载作用下桥上轨道会引起竖向振动,且振动频率与荷载速度有关,但桥上轨道振动频率与荷载移动速度的规律需要做进一步研究。
2)与静荷载作用相比,移动荷载作用情况下轨道结构的竖向振动振幅大大增加。
3)本文初步探讨了高速移动荷载特性对桥上轨道竖向位移的影响。研究结果表明,荷载移动特性会引起线路的竖向振动,对深入了解高速列车通过桥上轨道时的动力特性具有指导意义。
[1]李成辉.轨道[M].成都:西南交通大学出版社,2012.
[2]李江华.高速铁路钢轨平顺性的影响因素及其整治措施初探[J].现代交通技术,2011,8(3):90-93.
[3]王伟,曾京,罗仁.列车车轮不圆顺的研究现状[J].国外铁道车辆,2009,46(1):39-43.
[4]张格明.中高速条件下车线桥动力分析模型与轨道不平顺影响[D].北京:铁道部科学研究院,2001.
[5]张媛,程旭东,李静.轨道不平顺引起的车轨桥空间耦合振动分析[J].青岛大学学报,2008,23(3):72-77.
[6]傅一帆,罗雁云.道岔轨下刚度不均匀对轮轨系统动力特性的影响分析[J].铁道建筑,2011(4):139-141.
[7]翁长根,赫丹,王阳,等.扣件失效对城市轨道交通列车—浮置板式轨道系统竖向振动响应的影响[J].铁道科学与工程学报,2008,5(2):29-33.
[8]马伟斌,韩自力,朱忠林.高速铁路路桥过渡段振动特性试验研究[J].岩土工程学报,2009,31(1):124-128.
[9]雷晓燕.移动荷载作用下轨道基础刚度突变对轨道振动的影响[J].振动工程学报,2009,12(6):195-199.
[10]李成辉,万复光.高速铁路轨道位移波分析[J].铁道学报,1993,15(2):76-79.
[11]MICHALTSOS G,SOPHIANOPOULOS D,KOUNADIS A N.The effect of a moving mass and other parameters on the dynamic response of a simply supported beam[J].Journal of Sound and Vibration,1996,191(3):357-362.
[12]邓建良,吴定俊,李奇.简支梁桥动力系数的移动荷载列分析[J].工程力学,2012,29(10):177-183.
[13]肖新标,沈火明.移动荷载作用下的桥梁振动及其TMD控制[J].振动与冲击,2005,24(2):58-61.
[14]高淑英,沈火明.振动力学[M].北京:中国铁道出版社,2011.

