考虑初始几何缺陷的大跨度上承式钢管混凝土拱桥的非线性稳定研究
曾 勇,于 福,谭红梅
(1.重庆交通大学山区桥梁结构与材料教育部工程研究中心,重庆 400074;2.重庆交通大学山区桥梁与隧道工程省部共建国家重点实验室培育基地,重庆 400074;3.中交一航局第二工程有限公司,山东青岛 266071)
钢管混凝土拱桥按桥面在拱上的位置不同,分为上承式钢管混凝土拱桥、中承式钢管混凝土拱桥和下承式钢管混凝土拱桥[1]。钢管混凝土拱桥的主要受力构件以受压弯为主,且钢管混凝土拱桥随着跨径的增大,稳定问题更为突出。结构一旦发生失稳破坏,往往导致结构整体垮塌,带来极大的损失,其危害性往往比强度破坏更大。目前,国内外学者对钢管混凝土拱桥进行了广泛研究,但这部分研究大都针对中、下承式钢管混凝土拱桥,而对上承式钢管混凝土拱桥研究较少,目前仅见于文献[2-3],但文献[2]未研究非线性稳定。本文结合净跨430 m的某钢管混凝土拱桥,针对该桥跨度大、横向刚度较弱的特点,研究了上承式钢管混凝土拱桥的第二类稳定问题,得出了一些对设计和科研有意义的结论。
1 计算理论
在钢管混凝土工程实践中,恒载压力线与拱轴线的偏离、施工预拱度的设置、施工偏差导致的初始变形、非对称加载等因素使拱桥的失稳形态大部分属于第二类失稳。钢管混凝土拱桥随跨径的增大、材料强度的提高,在第二类失稳破坏时结构表现出大位移、大应变的特点,在实际试验研究中充分说明这一点[4]。因此在对钢管混凝土拱桥进行有限元分析时,应考虑结构的几何非线性、材料非线性,或双重非线性。拱的几何非线性属于弹性大变形问题,采用全量方法求解概念明确,易于理解。
拱桥结构的非线性平衡方程可写为[5]
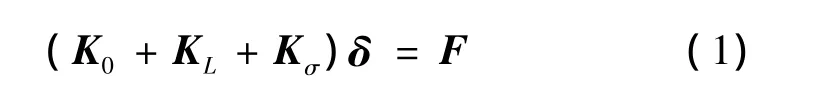
式中:K0为小位移线性刚度矩阵;KL为大位移矩阵;Kσ为初应力矩阵;δ为节点位移;F为等效节点荷载。另外,KL和Kσ是δ的函数,因此式(2)为非线性方程组。
非线性方程组的求解一般采用荷载增量法。荷载从0开始,按照某种增量形式逐步增大到λiF。当δ开始发散时,λiF即为拱桥极限承载力,可用Euler法,自修正Euler法等求解。如荷载增量步分得较细,可以偏于安全地认为前一级荷载为拱桥极限承载力,避免更加复杂的计算。
钢结构的本构关系采用刚塑性本构关系,现行钢桥设计规范对二类稳定安全系数尚没有明确规定。根据失稳破坏不得先于强度破坏的原则,采用边缘纤维屈服准则得到的不考虑荷载分项系数的整体稳定安全系数,应该大于容许应力安全系数,即对于钢结构最小稳定安全系数应该>1.7。混凝土的应力应变本构关系[6],按式(2)考虑,混凝土极限应变取0.003 5。
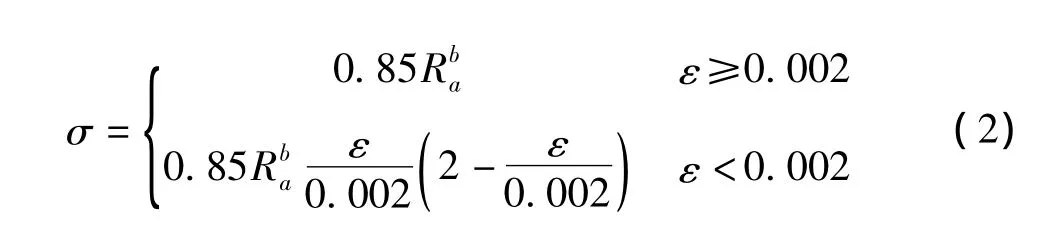
2 非线性稳定分析
2.1 工程概况
主拱圈采用钢管混凝土与钢管组成的桁架式断面,断面高度从拱脚13 m变化至拱顶6.5 m;单拱肋宽度4 m,由4根钢管组成,两单拱肋间中心距13 m。拱肋钢管外径1200 mm,最大管壁厚度35 mm。全桥立面图和主梁截面布置图分别见图1和图2。
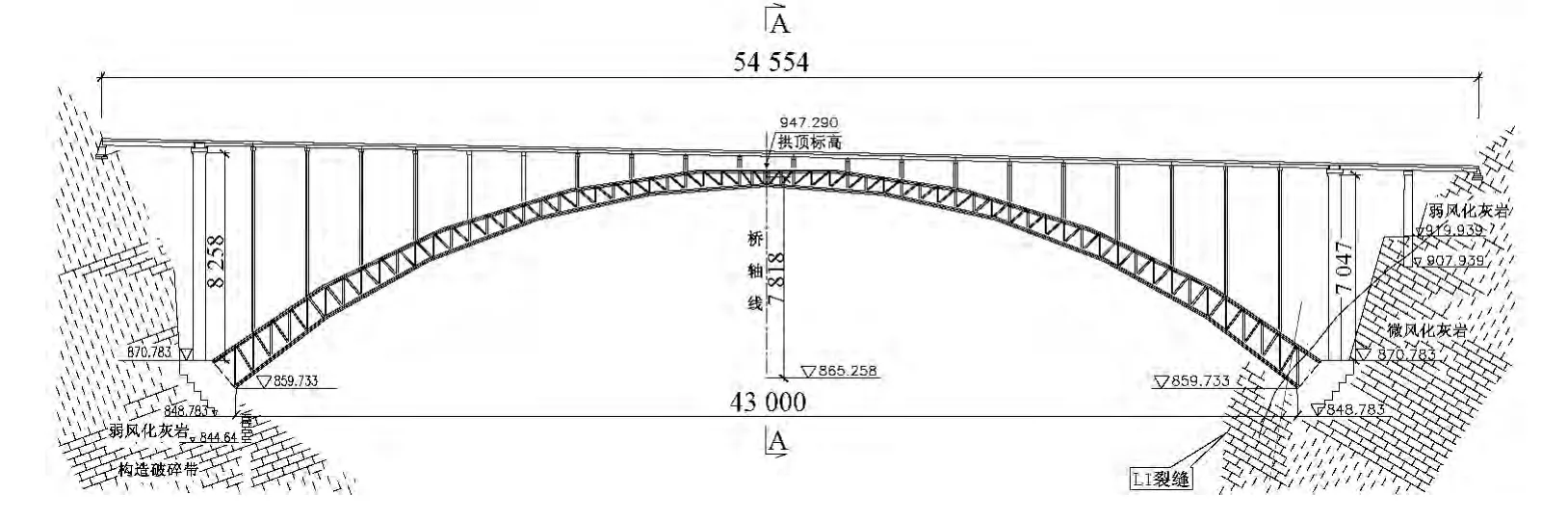
图1 全桥立面(单位:cm)
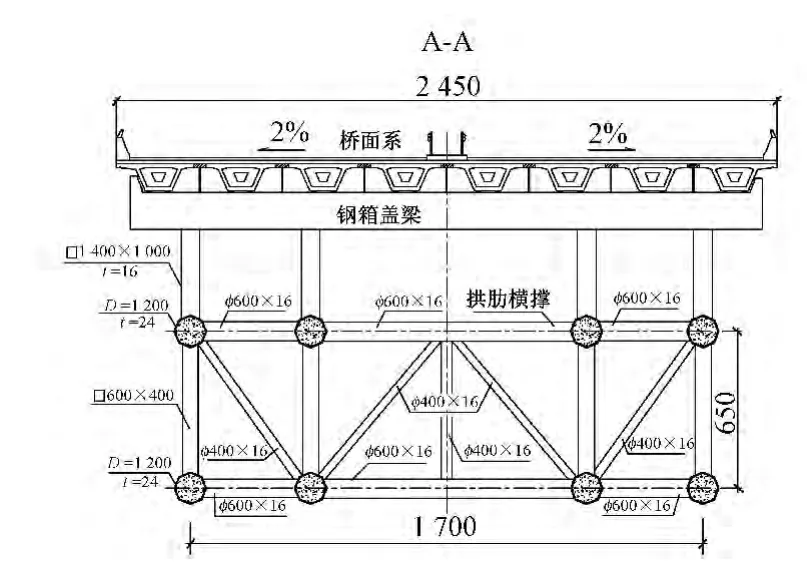
图2 主梁截面(单位:cm)
钢管混凝土拱肋截面由钢管与混凝土两种材料组成,本文不按换算截面法做等效转换[1],而是采用共用节点的分析模式,即将钢管混凝土模拟成钢管梁模型和混凝土梁模型,两种梁模型采用公共节点,保证钢管和混凝土的共同受力。
对于恒载,稳定系数定义为恒载的λ倍,即λg;对于活载则为相应活载的倍数,恒载不进行累加,即结构发生失稳时的荷载为g+λq。二类稳定分析采用的是考虑几何非线性和材料非线性的静力分析[7]。
2.2 计算工况
分析该桥成桥阶段的第二类稳定,先不考虑初始几何缺陷的影响,分为以下6种荷载工况:①桥梁恒载作用(工况1);②恒载+风荷载作用(工况2);③恒载+全跨满布公路—Ⅰ级汽车荷载作用(工况3);④恒载+左半跨满布公路—Ⅰ级汽车荷载作用(工况4);⑤恒载+右半跨满布公路—Ⅰ级汽车荷载作用(工况5);⑥恒载+全跨半桥宽满布公路—Ⅰ级汽车荷载作用(工况6)。
不考虑缺陷时各工况的分析结果见表1。
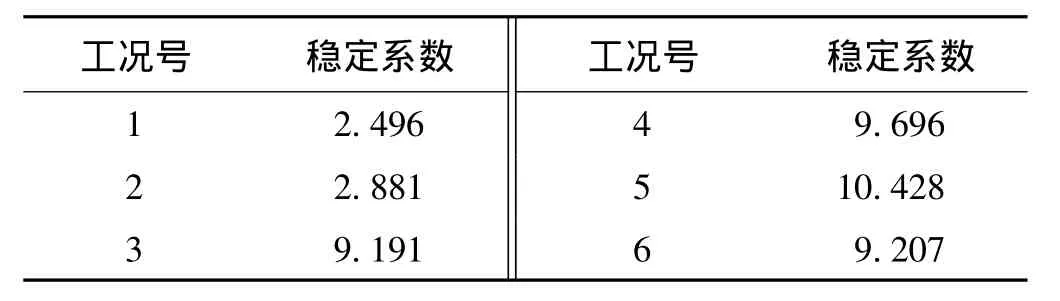
表1 不考虑缺陷的第二类稳定的稳定系数
3 考虑初始几何缺陷的非线性稳定分析
由于在制造、运输及安装等各施工环节中,拱肋会产生一定的变形,钢管成拱后的拱轴线往往达不到理想拱轴线,即拱肋存在初始的偏差。同时在结构自重及外荷载作用下,拱肋会产生附加的内力和变形。所以在钢管混凝土拱桥的建造过程中,不可避免地存在着初始几何缺陷。
稳定性分析考虑初始缺陷的大小为:第一种情况正对称初始几何缺陷,主拱圈横向偏移半个正弦波,最大位移为0.15 m。第二种情况反对称初始几何缺陷,主拱圈横向偏移一个正弦波,最大位移为0.15 m。考虑偏心的非线性稳定分析采用的假定和失稳判别准则同上节一致。在成桥阶段,对主桥结构进行第二类稳定分析,分别考虑正、反对称缺陷的影响,考虑的荷载工况与一类稳定一样。
在成桥阶段,对主桥结构进行第二类稳定分析,分别考虑正、反对称缺陷的影响,分为12种荷载工况。各种工况下二类稳定系数对比见表2。典型工况作用下的二类稳定失稳形态见图3。

表2 各种工况下二类稳定系数对比
从表2和图3可以看出,考虑了正、反对称偏心后,会降低结构的稳定系数。初始几何缺陷削弱了结构的刚度,增大了拱桥的初始几何缺陷弯矩。对应于工况1,初始几何偏心缺陷降低了拱桥结构的稳定性。不考虑初始几何偏心缺陷,稳定系数越低的工况,初始几何偏心缺陷则降低稳定系数的比例越少。但有趣的是,对于工况6,初始几何缺陷使得结构的稳定性有所提高,主要原因是施加初始几何缺陷的方向与全桥半幅汽车加载的方向相反,起着有利的作用。如果偏心施加的方向与全桥半幅汽车加载方向相同,稳定系数则会降低。
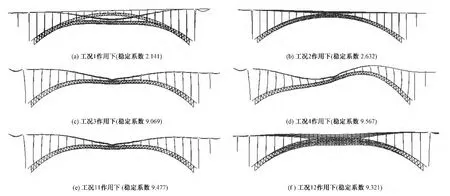
图3 第二类失稳形态示意
4 结论
1)通过考虑有正、反对称初始几何缺陷的第二类稳定分析,该大跨度上承式钢管混凝土拱桥在不同的工况下稳定系数均>2,满足相应的规范要求。
2)非线性因素对大跨度上承式钢管混凝土拱桥的稳定性影响显著,考虑非线性因素才能求得真正的稳定系数。各工况下结构的失稳形态与自重荷载工况类似,主要原因是结构自重为主要荷载,其它荷载的作用效应均小于自重引起的荷载效应。
3)考虑了正、反对称几何初始缺陷后,会降低结构的稳定系数。初始几何缺陷削弱了结构的刚度,同时也加大了荷载引起的初始几何缺陷弯矩,应当引起重视。
4)虽然正、反对称偏心不会改变结构的失稳形态,但会在一定程度上降低结构的稳定系数。
[1]陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,2000.
[2]赵河清,徐亮,杨惠林,等.大跨度上承式钢管混凝土拱桥的稳定性分析[M].公路交通科技,2006(11):82-85.
[3]曾勇,马如进,陈艾荣.大跨度上承式钢管混凝土拱桥的非线性稳定分析[J].上海公路,2008(2):50-53,64.
[4]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.
[5]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1996.
[6]过镇海.混凝土的强度和本构关系——原理与应用[M].北京:中国建筑工业出版社,1999.
[7]张兴春.钢管混凝土系杆拱桥施工关键技术及整体稳定性分析[J].铁道建筑,2012(8):5-7.

