硬弹簧Duffing隔振系统跳跃机理分析
楼京俊,张 晖,俞 翔,朱石坚
(1.海军工程大学 动力工程学院,武汉430033;2.船舶振动噪声重点实验室,武汉430033)
硬弹簧Duffing隔振系统跳跃机理分析
楼京俊1,2,张 晖1,2,俞 翔1,2,朱石坚1,2
(1.海军工程大学 动力工程学院,武汉430033;2.船舶振动噪声重点实验室,武汉430033)
硬弹簧Duffing系统在同一简谐激励下有时有多个周期解,并且系统能在这几个解之间来回跳动,也就是突跳。为精确找到系统随参数变化时产生跳跃的区间,先运用谐波平衡法分析系统的频率—振幅响应曲线和激励力幅值—振幅响应曲线,再通过预估—校正算法准确找到了系统随激励频率和激励力变化的跳跃区间,最后分别采用PMUCR胞映射方法和范德玻尔平面分析对所求得的区间加以验证,验证了所求得跳跃区间的精确性。
振动与波;Duffing;跳跃区间;预估—校正算法;胞映射;范德玻尔平面
非线性隔振系统具有与传统线性隔振系统不同的某些特点和性能,并且当参数处于一定范围内时,系统将呈现混沌运动状态,非线性隔振系统在其混沌状态下具有较好的隔振性能并能有效控制线谱成分[1,2]。Duffing系统是非线性隔振系统最基本模型之一,提出至今已有近90年的历史,最初是由G.Duffing[3]采用迭代法求的近似解而得到。1922年Hamel[4]总结了Duffing的研究,以单摆为研究对象,与G.Duffing的研究方法不同,Hamel没有将恢复力表示成线性项和立方项,而是用变分法获得幅频特性曲线,得到更精确的结果。1976年Holmes和Rand[5]的文章阐明了Duffing方程的分岔和突变理论。Ueda[6,7]发表了立方非线性恢复力Duffing振子的混沌动力学行为的文章。1995年黄桂玉[8]利用Melnikov函数讨论了Duffing系统次谐波振动,给出了精确估计的参数区域。1997年毕勤胜、陈予恕等[9,10]利用转迁特性求出Duffing模型主共振解、倍周期分岔转迁集的表达式。2008年钱长照[11]使用改进的L-P方法研究了强非线性Duffing系统受简谐激励作用下的主共振和1/3亚谐共振解。唐元璋[12]等简化了一种求取非线性常微分方程高阶谐波解的近似解析计算方法。以上研究在分析Duffing系统产生跳跃和分岔机理方面涉及较少,虽然张小龙、东亚斌[13]对Duffing隔振系统的力传递率及跳跃现象进行了理论分析,却没有得到精确跳跃区间。Duffing系统产生跳跃,即是系统发生了鞍结分岔或切分岔,这与系统产生倍周期分岔联系紧密,倍周期分岔又是系统通往混沌的道路之一,因而对Duffing系统跳跃的研究十分有意义。本文先运用谐波平衡法分析系统的频率—振幅响应曲线和激励力幅值—振幅响应曲线,再通过跟踪延拓算法准确找到系统分别随激励频率和激励力变化的跳跃区间,最后分别采用PMUCR胞映射方法和范德玻尔平面分析对所求得的区间加以验证。
1 Duffing系统模型
非线性隔振系统如图1所示,该系统的运动微分方程为

式中K1X+K3X3为非线性弹性恢复力;K3为负时,系统呈现软特性;K3为正时,系统呈现硬特性。

图1 非线性隔振系统
对方程(1)进行无量纲化,得

前者称为硬弹簧Duffing方程,后者称为软弹簧Duffing方程。式中
2 振动响应分析
对于硬弹簧Duffing系统(2),当激励力不是很大时,系统的受迫振动以频率为ω的振动占主导地位,令其解为:并取进行谐波平衡,可得频率—振动响应关系如下


图2 频率—振幅响应分析曲线

图3 激励力幅值—振幅响应曲线
3 跳跃分析
由于前面进行谐波平衡时仅取了1阶,只对基频进行了平衡。因而图2、3所示曲线只能大概反应频率—幅值、激励力幅值—振幅之间的关系。为得到准确的上跳、下跳点,采用4阶Runge—Kutta方法求得系统的Poincaré映射,作出Poincaré映射点的某个坐标随控制参数ω或f的变化曲线,便构成了分岔图。采用最简单的跟踪延拓算法,即,将在(或fk)求得的解直接作为 ωk+1=ωk+Δω(或fk+1=fk+Δf)时的初始条件。对方程(2)分别取控制参数ξ=0.1,f=0.5和ξ=0.1,ω=2进行分岔分析,可以得到分岔图如图4、5所示。
由上面数值分析可得,取ξ=0.1,f=0.5时,ω在1.44~2.21范围内,系统会因初值不同而在大小振幅上跳动。
由上面数值分析可得,取ξ=0.1,ω=2时,f在0.4~2.3范围内,系统会因初值不同而在大小振幅上跳动。
4 胞映射分析
徐皆苏[14](C.S.Hsu)在上个世纪80年代提出了胞映射方法。胞映射法在分析动力系统性态时,可以模拟周期运动时间历程曲线,准确地绘制出周期运动的渐进吸引域,通过对胞之间转移关系的研究完成对原动力系统的相应研究,揭示出系统的全局性态。

图4 系统(2)随ω变化分岔图(取参数ξ=0.1,f=0.5)

图5 系统(2)随f变化分岔图(取参数ξ=0.1,ω=2)
(2)确定特性保持判定中的推荐距离dp。dp包括两个分量dx和dy,本文设定其分别为胞x和y方向边长的10-5,通过计算可知,精度可以满足要求;
(3)数值积分。采用ode 45(4或5阶Runge-Kutta)方法,这个方法是变步长方法,即可以根据指定精度,自动调整步长和步数。首先要建立微分方程组的描述文件,然后用ode 45命令设置初始条件和积分时间;
(4)如果连续k次以上映射出选定区域,或者在这条轨迹的性态确定之前,已经达到了预先设定的循环次数,就认为这条轨迹的性态是不确定的。本文把k设定为12;
(5)完成胞映射程序以后,就可以判断吸引子的吸引域了。
胞映射分析情况如图6、7所示。
从图6可以看出,图(a)、(d)中,当取ξ=0.1,f=0.5,ω=1.43、2.22时,在相平面上只有一个解的吸引域;而图(b)、(c)中,当ω=1.44、2.21时,在相平面上存在大小振幅相互交错的解。因此,当ω从小逐渐增大时,在2.22时向下跳跃;ω从大逐渐减小时,在1.44向上跳跃。所以,此时系统的跳跃区间在1.44~2.21之间,从而也验证了跟踪延拓算法分岔分析结果准确性。同理,在ξ=0.1,ω=2时,从图7也可以验证f在取值0.4~2.3时的跳跃情况。
5 范德玻尔(Vander Pol)平面分析
由前面分析可知,当ω取值在一定范围时,对应于每一个具体的ω值,振幅A可以取三个不同的值。可以证明振幅取中间值S的振动是不稳定的。为了研究振动的稳定性,将A和ω写成随时间缓慢变化的形式

式中a1和b1是随时间缓慢变化的函数。频率为ω的振动在相平面中的代表点以角速度ω旋转,而式(4)中的a1和b1是以频率ω绕坐标原点作顺时针旋转(如图8、9中的(b)所示),因此在以a1和b1为坐标轴的范德玻尔平面上,频率为ω的振动的代表点是不旋转的不动点。
从图8、9中胞映射图(a)和范德玻尔平面上的解图(b)能明显看出,当系统参数确定在跳跃区间上时,系统对初始值有很强敏感性。不论是从胞映射图,还是范德玻尔平面上的解图上可以看出,两个周期1吸引子的吸引域相互交错、相互缠绕,只要初始条件稍加改变,系统的运动性态会随之改变。

图6 方程¨+0.1˙+x+x3=0.5cosωt在不同ω下的初始条件分区图
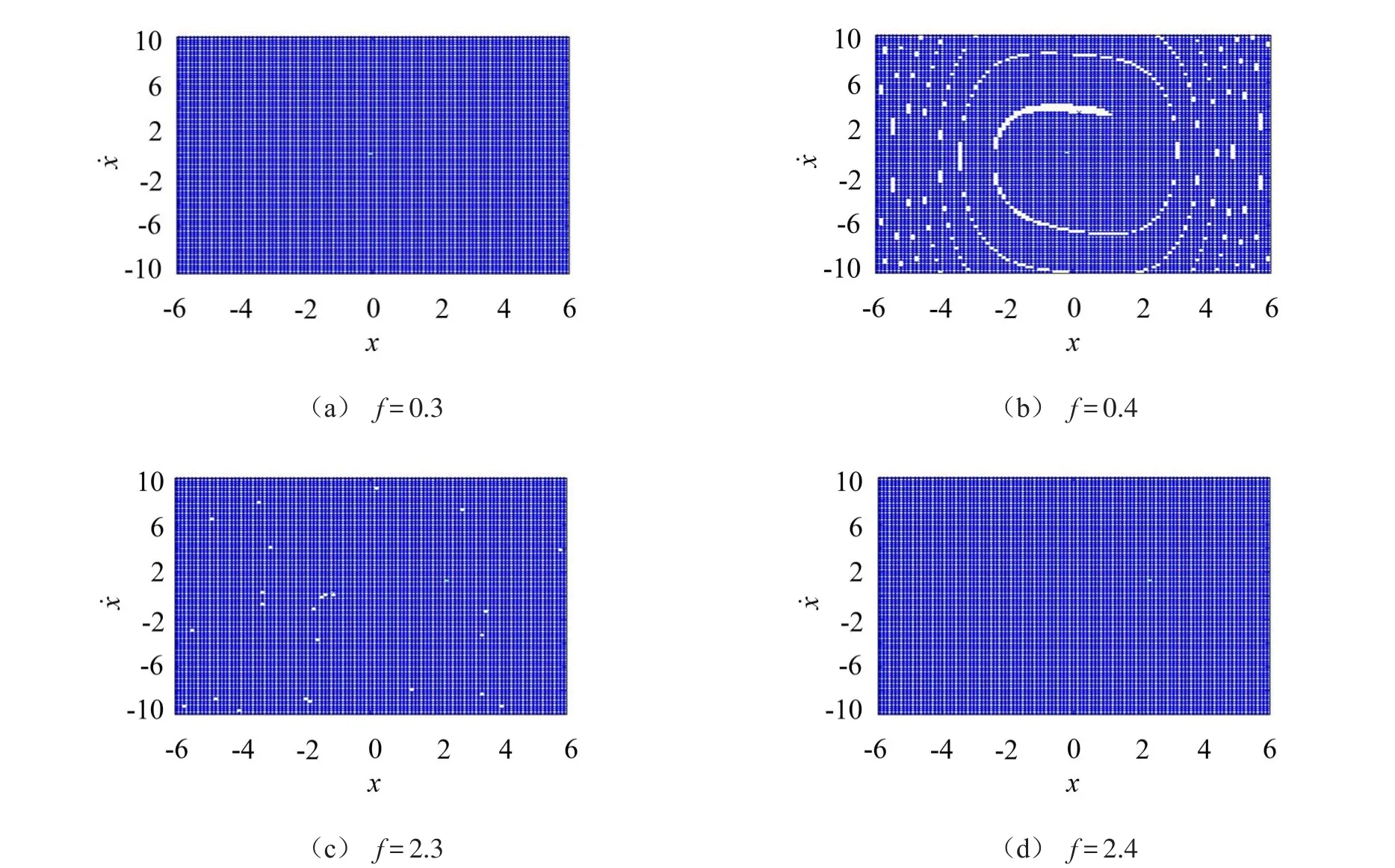
图7 方程¨+0.1˙+x+x3=fcos2t在不同f下的初始条件分区图

图8 方程¨+0.1˙+x+x3=0.5cos1.8t分析
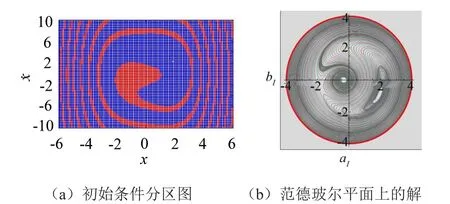
图9 方程¨+0.1˙+x+x3=1cos2t分析
6 结语
通过对硬弹簧Duffing系统分别随激励力和频率的变化,计算得到其产生跳跃的区间,结论如下:
(1)进行了幅频特性分析,得到了Duffing系统频率—振幅响应曲线和激励力幅值—振幅响应曲线图;
(2)通过跟踪延拓算法精确算出Duffing系统随激励力或激励频率变化时的跳跃区间;
(3)通过胞映射和范德玻尔平面上的解分析,验证了由跟踪延拓算法所求结果的准确性。
[1]楼京俊.基于混沌理论的线谱控制技术研究[D].武汉:海军工程大学,2006.
[2]刘树勇,位秀雷,许师凯,等.非线性混沌振动响应的试验分析[J].噪声与振动控制,2014,34(2):5-7.
[3]Duffing G.Erzwungene Schwingungen bei Veraderlicher EigenfrequenzundihreTechnischeBedeutung[M].Vieweg,1918.
[4]Hamel G.Über erzwungene schwingungen bei endlichen amplituden[J].MathematischeAnnalen,1922,86∶1-13.
[5]Holmes P J,Rand D A.The bifurcations of Duffing’s equation∶An application of catastrophe theory[J].Journal of Sound and Vibration,1976,44∶237-253.
[6]Ueda Y.Randomly transitional phenomena in the system governed by Duffing’s equation[J].Journal of Statistical Physics,1979,20∶181-196.
[7]Ueda Y.Random phenomena resulting from non-linearity inthesystemdescribedbyDuffing’sequation[J].International Journal of Non-Linear Mechanics,1985, 20∶481-491.
[8]黄桂玉.Duffing系统的次谐分岔[J].湖北大学学报,1995,17(2):161-167.
[9]毕勤胜,陈予恕.Duffing方程解的迁移集的解析表达式[J].力学学报,1997,29(5):573-581.
[10]毕勤胜,陈予恕,吴志强.强非线性Duffing系统倍周期分叉[J].振动工程学报,1997,10(2):183-189.
[11]钱长照.强非线性Duffing系统分岔相应分析的MLP方法[J].动力学与控制学报,2008,6(2):126-129.
[12]唐元璋,翁雪涛,楼京俊,等.非线性常微分方程高阶谐波平衡法傅里叶展开的简化[J].噪声与振动控制,2014,34(2):28-33.
[13]张小龙,东亚斌.Duffing型隔振的力传递率及跳跃现象的理论分析[J].振动与冲击,2012,31(16):38-42.
[14]Hsu C S.A theory of cell-to-cell mapping dynamical systems[J].J.Applied Mechanics,1980,147∶931-939.
Analysis of Snap-through Mechanism in Hard Duffing Vibration Isolation Systems
LOU Jing-jun1,2,ZHANG Hui1,2,YU Xiang1,2,ZHU Shi-jian1,2
(1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China; 2.National Key Laboratory on Ship Vibration and Noise,Wuhan 430033,China)
∶Hard Duffing vibration isolation system sometimes has several periodic solutions under the same harmonic excitation,and the system can bounce back and forth among the several solutions,which is known as snap-through.In order to find the snap-through regions accurately,the amplitude against frequency curve of the system and system amplitude against excitation amplitude curve are plotted by the harmonic balance method.Then,the snap-through regions of the system for different frequencies and excitations are obtained by trial and error method.Finally,the regions are verified to be accurate by PMUCR cell mapping method and Vandel pol plane analysis method.
∶vibration and wave;Duffing;snap-through region;trial and error method;cell mapping;Vandel pol plane
O175.14< class="emphasis_bold">文献标识码:ADOI编码:
10.3969/j.issn.1006-1335.2014.06.005
1006-1355(2014)06-0020-05
2014-05-05
国家自然科学基金资助项目(51179197);高等学校全国优秀博士学位论文作者专项资金资助项目(201057)
楼京俊(1976-),男,浙江义乌人,博士生导师,目前从事非线性动力学、振动与噪声控制研究。
张晖(1985-),男,湖北武汉人,研究生,目前从事非线性动力学、振动与噪声控制研究。
E-mail∶zh348688633@163.com

