柔性机械臂建模及动力学特性分析

刘旭亮，黄玉平，崔佩娟，徐祯祥

(中国航天科技集团公司 第一研究院 十八所，北京100076)

柔性机械臂建模及动力学特性分析

刘旭亮，黄玉平，崔佩娟，徐祯祥

(中国航天科技集团公司 第一研究院 十八所，北京100076)

以仿人手臂的三旋转关节刚柔耦合机械臂为研究对象，对柔性部分建立理论模型并分析其动态特性。为了提高模型精确度，利用有限段方法分析研究不同边界条件下柔性臂各阶固有频率及振型函数，通过假设模态法和汉密尔顿原理，考虑重力，建立机械臂柔性部分动力学模型。引入角度轨迹，在Matlab中利用四阶Runge-Kutta法求解非线性时变微分方程组，获得柔性臂末端负载的残余振动。为实现柔性机械臂模型的进一步精确化和主动残余振动控制提供参考。

振动与波；柔性机械臂；模态分析；弹性变形；动力学建模；振动分析

近几年，小型化、轻型化成为航天产品重要的发展方向；空间站建立、维护，空间垃圾回收以及深空探索是我国航天事业的发展目标。在当前形势下，传统大质量、大余量的刚性结构不能满足未来发展的需求，更加小型轻质、灵巧的机构设计及其控制方法是研究的重要方向之一。本文着眼于研究柔性体主动抑振控制方法，以仿人手臂的三旋转关节刚柔耦合机械臂为研究对象，建立模型并分析其动态特性，为后续控制方法的研究奠定基础。

柔性机器人手臂采用了低惯量的结构，具有以下潜在优点：更大的负载重量比、更低的经济成本、更少的能量消耗、更小的体积和更高的操作速度等。柔性机构带来轻质化等优点的同时，其最大的缺点是低刚度引起的振动。振动会严重影响定位精度和速度，甚至可能危及整个结构的安全。如何准确描述和正确处理系统中柔性结构带来的振动是柔性机械手臂的研究重点。近30年来，国内外学者在柔性机械臂相关领域发表了大量研究成果。2003年，宋秩民等人对柔性机械臂动力学分析与振动控制研究进行了综述分析。2006年Dwivedy和Eberhard回顾了1974—2005年间柔性机械臂领域的相关研究成果，内容涵盖柔性机械臂建模、动力学计算、控制与实验各个方面[1]。柔性臂主动振动控制的基础在于对柔性机械臂特性分析，针对不同对象的模态和动态特性分析十分重要。

1 柔性机械臂理论建模

3R刚柔耦合机械臂主动抑振控制方法研究试验台三维模型如图1所示，试验台由刚性部分和柔性部分组成，本文旨在分析末端柔性臂和负载的动力学特性。

图1 主动抑振控制方法研究试验台

试验台由一个水平面旋转关节底座和两个竖直面旋转关节组成。其末端为柔性臂—负载，静止时在重力作用下柔性臂带负载会发生初始形变。系统残余振动主要由柔性部分引起。因此，本文研究针对柔性臂和负载。

柔性体变形十分复杂，包含不同的耦合因素，用解析的形式表达十分困难，一般采用多种离散的方法[1]。假设模态方法将有限个假设模态振动的线性之和来近似描述弹性体的振动，把系统的惯性和弹性特性转化到一些振型上去，这些振型本身是物理坐标的确定函数。针对柔性臂—负载模型提出以下假设：

（1）柔性臂均质等截面；

（2）末端负载对称，柔性臂不发生扭转变形；

（3）柔性臂长度远大于截面半径，轴向伸缩变形近似为零。则柔性臂末端负载在空间中的变形量可以表示为

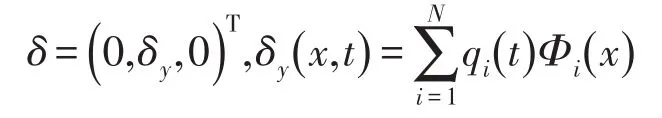
上式中qi(t)为模态坐标，Φi(x)为振型函数。根据假设模态理论，柔性臂任意位置t时刻的弹性变形都可以用N个模态坐标和振型函数的线性之和来描述。其中，振型函数由描述对象的固有特性决定，每1阶固有频率对应一特定振型函数[2]。

1.1 基于有限段的模态分析方法

为了能更准确的建立柔性部分模型，正确描述弹性变形，对柔性臂—负载进行模态分析，求解其各阶固有频率和相应的振型函数。考虑到柔性臂为均匀圆柱细长杆，基于有限段方法，建立柔性杆运动方程，带入边界条件后求解[3]。

柔性臂可以利用有限段方法离散成N个单元，每个单元长度为dL，每个单元的横向应变方程为u(x,t)，对于每一个单元，横向变形都可以表示为u(x,t)=C1+C2x+C3x2+C4x3，第一个单元两端的应变和应力如图2所示，第一个单元节点的边界条件

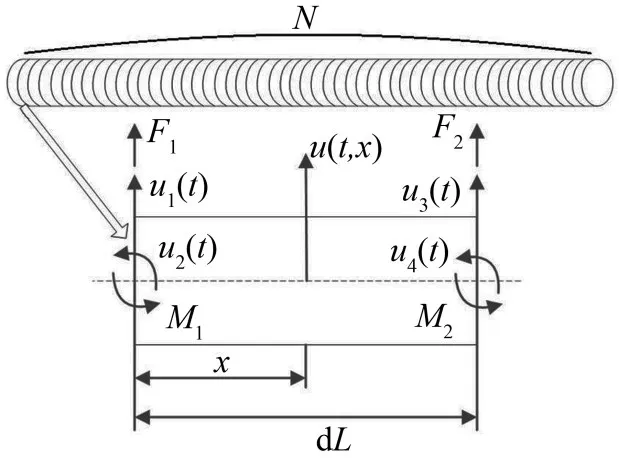
图2 基于有限段法柔性臂离散模型

上式中v1、v2分别表示第一个单元两端横向变形，θ1、θ2分别表示第一个单元两端偏转角度。F、M分别为剪力和转矩。第一个单元横向应变

则，单元势能和动能分别表示为

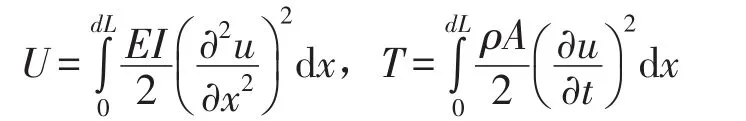
利用拉格朗日方程得到所有单元的振动方程都可以表示成

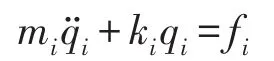
其中mi、ki分别为i单元的质量和刚度矩阵

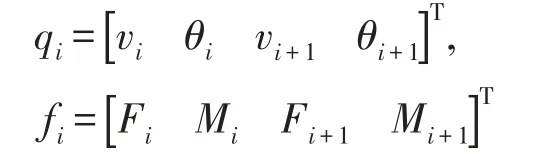
模型中每一个单元与相邻单元节点重合，可以将各个单元的振动方程组合起来得到整个柔性臂的运动方程

上式中

柔性臂末端负载和始端转轴材料为不锈钢，远大于柔性臂杨氏模量，可以将其看作集中质量点。集中质量点加在相应的单元上，在计算单元运动方程时，增加了单元总动能，令集中质量点质量为M，单元的动能变为

其中x′为集中质量在单元的位置。末端负载集中质量点加在第N个单元末端，即x′=dL，始端转轴集中质量点加在第一个单元中间位置，即x′=dL/2。添加集中质量后柔性臂自由振动方程为：

带入悬臂—负载边界条件，由悬臂条件可知A端第一个单元第一节点的变形和角度都为0，即U(1)=U(2)=0[4]。利用Matlab求解得到前4阶固有频率。

在Ansys 12.0的Model Analysis工具中建立图3模型。

图3 ，柔性臂Ansys模型

如上图所示，柔性臂模型左端固定，同时添加集中质量C（0.2 kg），右端自由，在端面上添加集中质量B（0.5 kg）。两种方法结果对比如下。

表1 有限段法和Ansys计算固有频率对比

对比结果显示两种方法得出的前4阶固有频率基本一致，两种方法得到的各阶模态振型如下：

每个模态振型相当于一组坐标，因此振型乘以任意非零系数都可以作为这1阶模态的振型[5]。对比图4、5两种不同方法计算结果，有限段法和Ansys软件计算的振型结果基本一致，本文利用五次多项式拟合有限段方法得出的振型，得到各阶振型函数

1.2 动力学模型

柔性臂和负载可以简化成以下模型。

如图6所示，坐标系X0OY0为基坐标系，X1OY1为关节坐标系，X0为重力方向，X1指向柔性臂未发生变形时的轴线方向，dy为末端负载偏移量，方向垂直于X1，关节转角为q。本文选取假设模态法的截断频率为2阶，即柔性臂的变形可以表示成[6—8]

图4 基于有限段方法前4阶振型

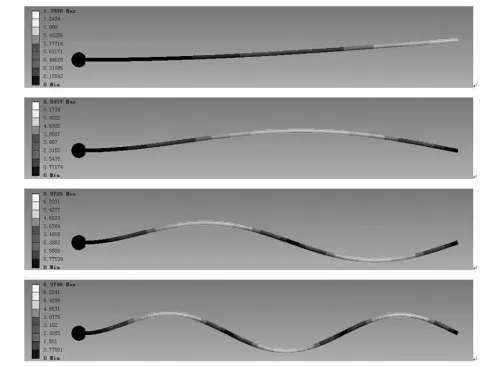
图5 基于Ansys前4阶振型

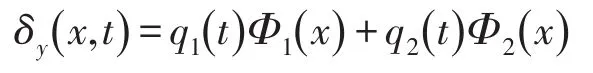
图6 柔性臂—负载简化模型

柔性臂长度为l，则柔性臂上任意一点在基坐标系下的位置向量为

首先，不考虑重力，即柔性臂与负载重力势能为零。令柔性臂密度为ρ，横截面积为A，杨氏模量和截面惯性矩分别为E、I，末端负载质量为m，则负载的动能

柔性杆自身动能

柔性杆的弹性势能

令T为系统动能，U为系统势能，W为虚功，根据汉密尔顿原理可知

柔性杆末端负载的动能

柔性杆自身动能

柔性杆的弹性势能

系统虚功

将上述方程带入哈密尔顿方程中，令含有δq1和δq2项的系数为0，得到柔性臂动力学方程

其中

考虑重力时，向系统中加入柔性杆重力势能Epl，末端负载重力势能Epm。

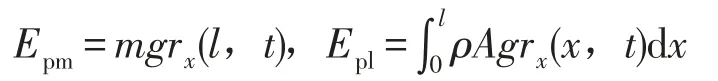
其中rx为位置向量r在X0轴方向分量，系统势能为U=Eul+Epl+Epm，同理可得柔性臂动力学方程。

上文中参数定义

2 仿真结果

在Matlab中建立柔性臂动力学模型，令负载质量为0.5 kg，重力加速度为9.8 m/s2。柔性臂参数如下表。

表2 柔性臂参数

为了能够清晰的反映柔性臂的残余振动，仿真输入关节角度期望从初始角度θ0到终止角度θ1，用时T。引入角度轨迹方程当时

带入基于有限段法的模态分析得到的前两阶振型函数、柔性臂参数以及关节输入角度轨迹，利用4阶Runge-Kutta法分别求解不考虑重力和考虑重力情况下，柔性臂末端弹性变形的前两阶模态坐标，得到柔性臂末端负载运动情况

如图7所示，当关节角度θ耗时从1 s从0度变化到45度，由于惯性力和角加速度作用，柔性臂末端先出现负向偏移，再向正向运动，当关节到达终点时，机械臂末端产生有初始状态的自由振动，在无阻尼情况下继续等幅振动。对比有、无重力的仿真结果，重力会改变振动峰值和稳态偏差，但对残余振动的频率等柔性臂固有特性没有影响。

由悬臂梁绕度方程可知，最大绕度可以表示为

式中l为悬臂梁长度，E、I分别为杨氏模量和截面惯性矩，m为负载质量。带入仿真柔性臂参数，得ωmax=-0.055 m。在考虑重力的仿真结果中，自由振动的振动中心位置（稳态偏差）为-0.057 m，与最大绕度基本一致。

考虑重力情况下，柔性臂末端运动及前2阶模态坐标如下图。

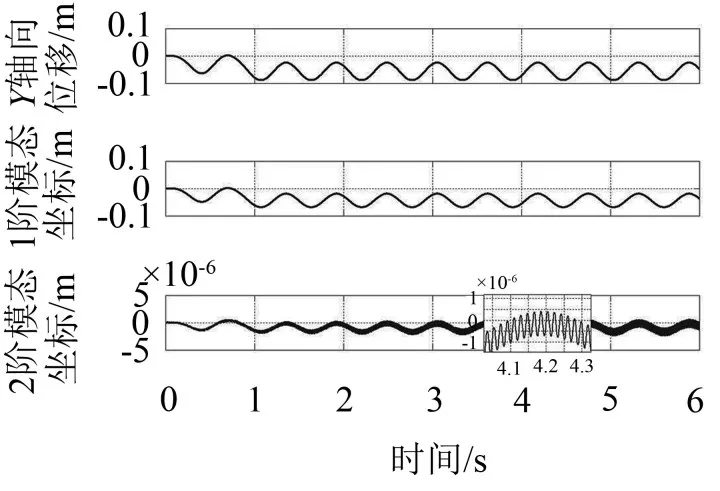
图8 仿真前2阶模态坐标

由上图可以看出1阶模态坐标频率与柔性臂末端运动频率和波形相似，幅值远小于1阶模态坐标；2阶模态坐标存在波形叠加现象，其中一种和1阶模态频率近似，另一种频率较高。对2阶模态坐标做频谱分析，确定它的包含的主要频率波形。

图9显示2阶模态坐标中主要含有两种频率波形，频率分别为f1=1.76 Hz，f2=46.9 Hz，f1与柔性臂1阶固有频率和1阶模态坐标频率一致，f2与柔性臂2阶固有频率近似。

仿真分析结果显示，前文建立的动力学模型能够较为准确的描述柔性臂运动状态，可以作为后续残余振动主动控制状态方程的基础；重力对柔性臂的影响不可以忽略，对柔性臂的振动峰值和稳态偏差影响很大。

3 结语

本文针对3R刚柔机械臂试验台的柔性臂部分，建立动力学方程，为了准确的描述柔性变形，用有限段方法分析柔性臂模态，得到其各阶固有频率和振型。分析结果与Ansys仿真软件对比，两种方法结果一致。

通过汉密尔顿原理建立柔性臂动力学方程，在描述弹性变形的假设模态方法中引入了有限段方法拟合出的振型函数。带入柔性臂实际参数，仿真分析了已知角度轨迹输入下柔性臂末端负载的运动情况，通过动态过程分析和静态偏差对比，初步证明模型的正确性。

图9 2阶模态坐标频谱分析

根据仿真结果，分析了残余振动的组成，为3R刚柔机械臂的建模和振动控制打下基础。

文中，模型建立和仿真求解过程中考虑了非线性因素，模态坐标存在耦合现象。耦合现象会对后续的主动抑振控制带来影响，因此控制模型的建立需要进一步解耦；耦合现象存在的另一种可能是振型选取不准确，在模态分析过程中，边界条件选取正确与否决定了模型的正确性，作者也将铰接——自由和旋转——自由两种边界条件带入模态分析，得出相应的固有频率和振型函数，这种情况下会出现零阶振型，在将振型函数引入动力学模型后求解结果有明显错误。因此对柔性臂模态分析过程中边界条件的选取和描述，有必要更进一步的研究。

[1]Dwivedy.Dynamic analysis of flexible manipulators,a literature review[J].Mechanism and Machine Theory.2006,41∶749-777.

[2]Singiresu S.Rao.Mechanical Vibrations[M].北京：清华大学出版社，2009，439-452.

[3]张策.机械动力学[M].北京：高等教育出版社，2000，120-124.

[4]崔佩娟.带有动力减震器的柔性机械臂的振动及其主动控制[D].北京：北京科技大学，2008.

[5]清华大学工程力学系.机械振动[M].北京：机械工业出版社，1980.311-389.

[6]H.R.Heidari.A new nonlinear finite element model for the dynamic modeling of flexible link manipulators undergoing large deflections[R].International Conference on Mechatronics.Istanbul,Turkey.April 13-15,2011∶375-380.

[7]蒙树立，熊静琪，吕志刚.折叠式高空作业车臂架系统的动力学建模[J].噪声与振动控制，2012，32(4)：63-67.

[8]谢向荣.柔性板基础隔振系统的柔性多体动力学理论建模[J].噪声与振动控制，2010，30(6)：58-62.

Modeling and Dynamic CharacteristicAnalysis of Flexible RoboticArm

LIU Xu-liang,HUANG Yu-ping,CUI Pei-juan,XU Zhen-xiang

(The 18 th Institute,ChinaAcademy of Launch Vehicle Technology,Beijing 100076,China)

∶Taking humanoid rigid-flexible coupling robotic arm with three rotating joints as the object,the dynamic model of the flexible part of the robotic arm is established and its dynamic characteristic is analyzed.For improving the accuracy of the model,the finite segment method is used to analyse the intrinsic frequencies and vibration-mode functions of the flexible part of the robotic arm with different boundary conditions.The gravity effect is considered and the modal-assumption method and Hamilton’s principle are used to describe the deformation of the flexible shaft.Introducing the angular function of the joints,the 4th order Runge-Kutta method is utilized to solve the time-varying non-linear differential equations by means of MATLAB code.The residual oscillation of the loaded flexible arm end is derived.This research has provided a foundation for refinement of the flexible robotic arm model and for the active control of the residual oscillation.

∶vibration and wave;flexible robotic arm;modal analysis;elastic deformation;dynamic model;oscillation analysis

ADOI编码：10.3969/j.issn.1006-1335.2014.06.002

1006-1355(2014)06-0007-05

2014-04-08

863项目：机电作动子系统关键技术攻关及研制（2012AA70607051）

刘旭亮（1990-），男，新疆乌苏人，硕士研究生，主要研究方向：机电一体化，机械动力学。

黄玉平，男，研究员，硕士生导师。

E-mail∶huangyuping18@126.com