薄壁圆柱壳在纯弯曲下的非线性自由振动
顾建祖,欧晓林,李龙元,虞 波,李 康
(1.江苏大学 土木工程与力学学院,江苏 镇江212013;2.普利茅斯大学 海洋科学与工程学院,普利茅斯 英国PL48AA)
薄壁圆柱壳在纯弯曲下的非线性自由振动
顾建祖1,欧晓林1,李龙元2,虞 波1,李 康1
(1.江苏大学 土木工程与力学学院,江苏 镇江212013;2.普利茅斯大学 海洋科学与工程学院,普利茅斯 英国PL48AA)
分析了薄壁圆柱壳在纯弯曲下的非线性自由振动。基于改良的Brazier简单理论,将圆柱壳的纯弯曲变形简化为以下两个阶段:第一阶段壳体没有弯曲,横截面由圆形变成椭圆形;第二阶段壳体是横力弯矩作用下的变截面梁。通过Brazier简单理论获得壳体的应变能,然后利用拉格朗日方程求得薄壁圆柱壳的几何非线性自由振动方程,最终得到自由振动频率,并对线性解与非线性解进行对比分析。
振动与波;自由振动;非线性;拉格朗日方程
随着科学技术的不断进步,航天航空和船舶等工业中所使用的圆柱壳越来越薄,所以薄壁圆柱壳的静态或动态分析已成为现今的研究重点。由Brazier简单理论可知,壳体的横向弯曲和横截面的椭圆化耦合将产生附加的应变能,从而使得壳体非线性振动。
1874年Aron的弹性力学方程中第一次提到了薄壁圆柱壳,而薄壁圆柱壳弯曲的简单理论是在1927年Brazier[1]首次提出的。Brazier指出当直管处于纯弯曲情况时,弯矩会使管的横截面趋向扁平化或椭圆化,这会导致壳体抗弯刚度的减小,随着弯矩的增加,抗弯刚度进一步降低,弯矩将存在一个最大值。但这一理论仅适用于无限长圆柱壳,直到1965年,Aksel’rad[2,3]通过Valasov的半膜结构理论确定壳的横截面变形对屈曲行为的影响,才将Brazier简单理论应用到有限长壳体中。1997年,A.Lakis[4]等人将薄壳理论和有限元方法结合起来,研究了正交各向异性层合圆柱壳的非线性自由振动,并指出有限元—经典薄壳理论的结合方法不仅比现有理论精确,还可以获得高精度的频率。1999年,李龙元[5]分析了加筋圆柱壳的屈曲和非线性弯曲响应,他指出因为钢筋可以抵抗椭圆化变形,提高了整个壳体的抗弯刚度,所以临界弯矩随着钢筋数目和刚度的增加而增加。2003[6]年高传宝、张维衡等用波传播的方法分析了复合材料层合圆柱壳的振动。2005年肖汉林、刘土光[7]等研究了复合材料纵横加筋圆柱壳自由振动。2009[8]年顾红军、郭盛鹏分析了受冲击圆柱壳的非对称屈曲分析。2009年王巍[9]研究了弹性圆柱壳结构振动有源控制,采用不同控制策略,对圆柱壳结构振动进行有源控制,并结合二次最优理论建立圆柱壳振动有源控制理论模型,得出了不同控制策略下的最优次级力。
1 物理模型
当薄壁圆柱壳受到横力弯矩时,中性面两侧的纵向拉伸与压缩应力使得截面成椭圆形,因此,壳体的变形可以看成横向弯曲变形和横截面椭圆化变形两个阶段。
如图1所示的圆柱壳长为L,平均半径为R,厚度为h。壳体曲面上任一点的轴向、切向和径向位移分别记为u(x,θ,t),v(x,θ,t)和w(x,θ,t),θ是该点所在半径与z轴的半径之间的角度。
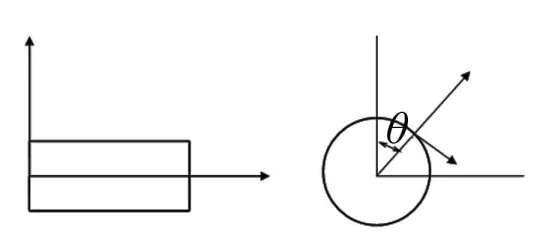
图1 柱壳的几何形状及坐标
壳体受到横力弯矩时,位移表示为

其中位移u1(x,t),v1(x,t)和w1(x,t)表示壳体横向弯曲的变形位移,而u2(x,t),v2(x,t)和w2(x, t)表示壳体横截面椭圆化的变形位移。
薄壁圆柱壳的应变能和动能可以表示为[5]

其中ρ为壳体的密度,Ex为壳体轴向的弹性模量,Gxθ为壳体的剪切模量,Dθ为壳体单位周长的抗弯刚度,U1是第1阶段的应变能,U2是第2阶段应变能。
考虑到薄壁圆柱壳的简支边界条件,w(x,θ)=0(当x=0,x=L)。横截面形状约束v(x,θ)= 0(当x=0,x=L)。杆端刚性旋转u(x,θ)=ΩRcos θ,(当x=0,x=L)(Ω为旋转角)[5]。位移按傅里叶级数展开如下(因为壳体受纯弯曲,占主导地位的变形是弯曲变形,且为了简化繁杂的计算过程,这里只取第一项)
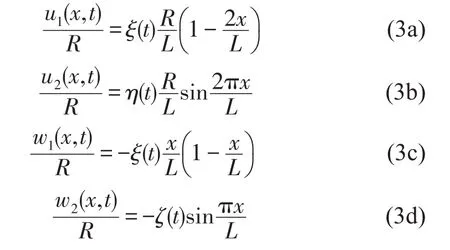
2 非线性振动求解
将方程(3a)至方程(3d)代入方程(2a)至方程(2c),由拉格朗日方程求得
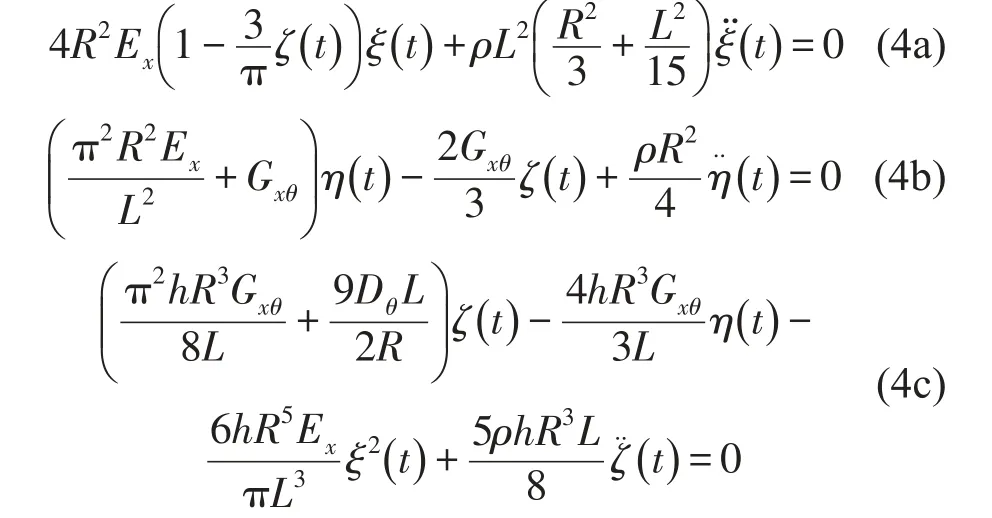
忽略非线性项,方程(4a)、(4c)简化为
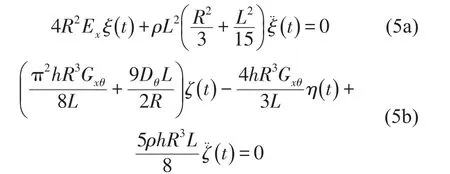
由此可以解得自由振动频率ω1,ω2和ω3(此为线性解)。
假设ξ(t)=ξ1(t)+ξ2(t)(此为非线性解),ξ1(t)= ξlin(t)=非线性解中的线性部分,ξ2(t)=ξnon-lin(t)=非线性解中的非线性部分,并且ξ(t)=ξlin(t),则方程(4a)简化为
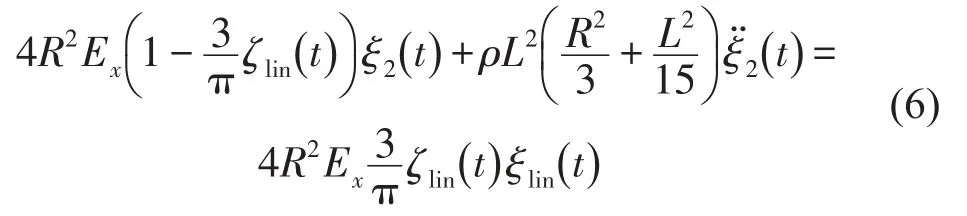
由于因为ξlin(t)和ξ2(t)非常小,所以他们的乘积远小于方程(6)中的其他项,方程(6)可简化为
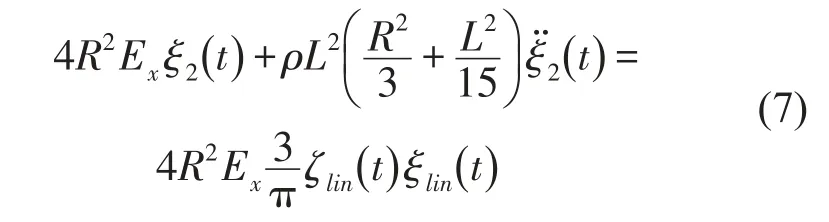
假设壳体自由振动为
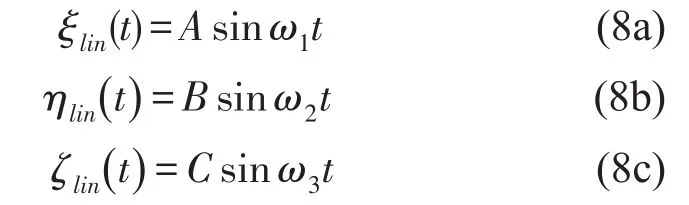
其中,A、B、C为壳体振幅。
方程(7)可化为
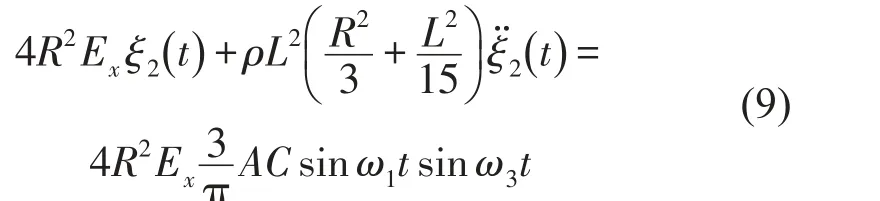
利用初始条件ξ2(0)=0,=0解得ξ2(t)的一次渐近解
3 算例
薄壁圆柱壳的各项参数见表1,取R=0.100 m,此时R/h=100,改变C得到如图2-5所示的线性解与非线性解曲线。
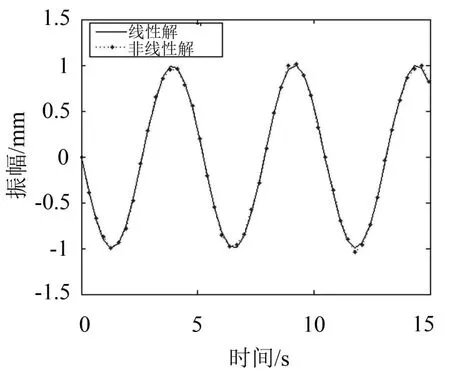
图3 线性解与非线性解(C=0.1)
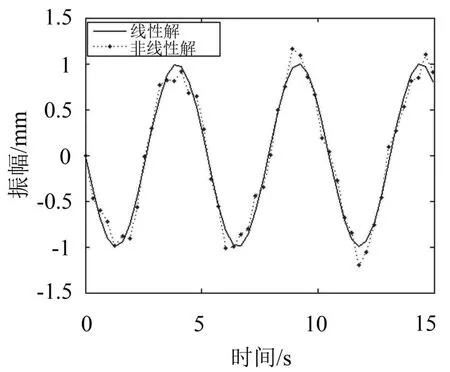
图4 线性解与非线性解(C=0.5)

图5 线性解与非线性解(C=1)
取C=0.1,改变薄壁圆柱壳的半径R,即改变薄壁圆柱壳的R/h。图6、7分别是R/h=25、300时的线性解与非线性解曲线;

表1 薄壁圆柱壳参数
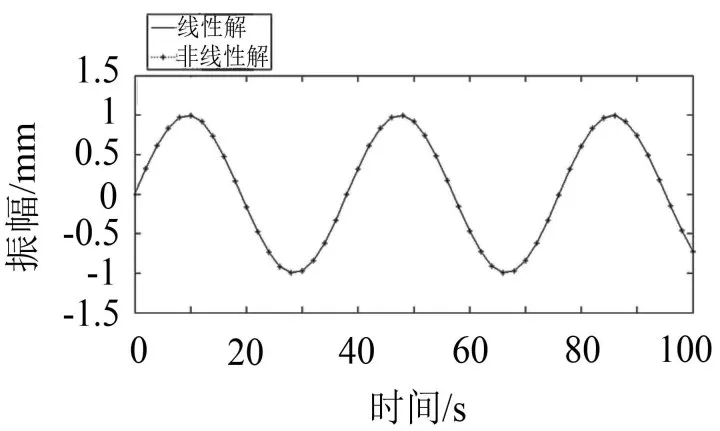
图6 线性解与非线性解(R/h=25)

图7 线性解与非线性解(R/h=300)
4 讨论与结语
4.1 参数C对非线性振动的影响
由图2—图5可知,当C的值较小时,线性解与非线性解基本吻合,此时的非线性影响较小,可以用线性解近似代替非线性解;当C的值较大时,线性解与非线性解相差较大,非线性影响不能忽略;综上所述:薄壁圆柱壳变形越大,线性解与非线性解相差越大。
4.2 参数R/h对非线性振动的影响
由图3、图6以及图7可知,当R/h=25时,线性解与非线性解吻合的相当好;当R/h=100时,线性解与非线性解曲线吻合度虽然没有R/h=25时好,但差别也不是很大;当R/h=300时,线性解与非线性解相差很大,此时不能再用线性解近似代替非线性解。综上所述,薄壁圆柱壳的壁厚越薄,线性解与非线性解相差越大。
[1]Brazier L.G.On the flexture of thin cylindrical shells and other thin sections.Proc.R.Soc.Ser.A,London,UK 1927,116∶104-114.
[2]Aksel’rad E.L.Pinpointing the upper critical bending load of a pipe by calculating geometric nonlinearity.Izv.Akad.Nauk SSR Mekh.1965,4∶133-139.
[3]Aksel’rad E.L.,Emmerling F.A.Collapse load of elastic tubes under bending.Isr.J.Technol.1984,22∶89-94.
[4]A.A.Lakis,A.Selman and A.Toledano.Non-linear free vibration analysis of laminated orthotropic cylindrical shell.Elsevier Science Ltd,Quebec.1997,1∶27-49.
[5]Long-yuan Li.Nonlinear bending response and buckling of ring-stiffened cylindrical shells under pure bending.Birmingham B4 7ET,UK.1999,39∶765-781.
[6]高传宝,张维衡,戴起生.用波传播方法分析复合材料层合圆柱壳的振动[J].噪声与振动控制,2003,6:1-4.
[7]肖汉林,刘土光,张涛,等.复合材料纵横加筋圆柱壳自由振动分析[J].噪声与振动控制,2005,6:4-7.
[8]顾红军,郭盛鹏.受轴向冲击圆柱壳非对称屈曲分析[J].噪声与振动控制,2005,3:12-15.
[9]王巍.弹性圆柱壳结构振动有源控制理论分析[J].噪声与振动控制,2009,3:23-26.
Nonlinear Free Vibration of Thin-walled Cylindrical Shells under Pure Bending
GU Jian-zu1,OU Xiao-lin1,LI Long-yuan2,YUBo1,LIKang1
(1.School of Civil Engineering and Mechanics,Jiangsu University,Zhenjiang 212013,Jiangsu China; 2.School of Ocean Science and Engineering,University of Plymouth,Plymouth PL48AA,UK)
∶The non-linear free vibration of thin-walled cylindrical shells under pure bending is analyzed.Based on the modified Brazier simple theory,deformation of the shell subjected to pure bending can be simplified to two stages.One is that the sections of the shell become elliptic but its axis remains straight;the other is the transverse bending deformation with the shell regarded as a beam with variable elliptic sections.The strain energy of the shell can be obtained based on the Brazier simple theory,and the non-linear free vibration equation of the thin-walled cylindrical shells will be derived by the Lagrange equation.As a result,the free vibration frequency is obtained,and the linear and nonlinear solutions are compared mutually.
∶vibration and wave;free vibration;nonlinearity;Lagrange equation
O422.6< class="emphasis_bold">文献标识码:ADOI编码:
10.3969/j.issn.1006-1335.2014.06.007
1006-1355(2014)06-0029-04
2014-03-05
顾建祖(1961-),男,江苏大学土木工程与力学学院,副教授,主要从事振动测试、智能材料与结构的研究。
E-mail∶gjz@ujs.edu.cn

