复杂结构体的声辐射模态远场计算方法
鱼海涛,王英民,王 奇,苟艳妮
(1.西北工业大学 航海学院,西安710072;2.西安科技大学 理学院,西安710054)
复杂结构体的声辐射模态远场计算方法
鱼海涛1,2,王英民1,王 奇1,苟艳妮1
(1.西北工业大学 航海学院,西安710072;2.西安科技大学 理学院,西安710054)
声辐射模态在主动结构声控制领域取得了满意的噪声控制效果,但缺乏有效简便的远场测量或计算方法已成为其进一步发展的瓶颈。基于远场封闭包络与结构表面辐射声功率相等,借助声传递矩阵的概念,将声辐射模态的求解转换到流体域进行求解,获得了一种通用的任意结构远场声辐射模态求解方法。为了验证方法的可行性,利用不同的场点包络形状、不同距离的场点以及不同的场点数目对其性能进行分析,主要包括结构辐射声功率、声辐射模态幅值、声辐射模态效率。利用获得的声辐射模态计算脉动球的辐射声功率,并与其理论解进行比较,计算结果显示不同的场点状态对辐射声功率的影响较小,所获取的声辐射模态和辐射效率具有较高的可信度。同时,本方法可为远场测量声辐射模态提供理论参考。
声学;声辐射模态;声传递矩阵;边界元方法;辐射功率;辐射效率
声辐射模态(ARM)自20世纪90年代由Borgiotti[1]、Sarkissian[2]、Elliott[3]及Cunefare[4,5]等人提出以来,在主动结构声控制(Active Structural Acoustic Control,简称ASAC)领域取得了满意的噪声控制效果。与振动模态相比,因其仅与结构的形状、尺寸及研究频率有关,而与结构的材料、边界条件及激励力的属性无关,且消除了各阶声辐射之间的相互耦合[6],国内外学者对于ARM进行了持续的关注和研究。
姜哲[7]通过一线性自伴正算子确定了一组基函数作为声辐射模态,但其所构造的基函数仅对板状结构有明确的物理意义。由于边界元方法(Boundary Element Method,简称BEM)更适合任意三维结构的求解,基于BEM的声辐射模态计算方法得到了更多的关注。
黎胜等[8]将CHIEF方法用Moore-Penrose广义逆引入到声辐射模态公式中,给出了正方形封闭空间结构声辐射模态的辐射效率和形状。赵志高等[9]将边界元方法与广义特征值的理论结合研究了球体和立方体的声辐射模态。沈火明等[10]基于非协调边界元法研究了球体和立方体的声辐射模态。张晓宇等[11]采用对壳体两端分别延长2个肋位的方法,利用商业软件SYSNOISE分析比较了圆锥壳和圆柱壳的声辐射模态特性,但对于球体、立方体等无端或多端结构则无法采用此方法进行计算,同时由于几何形状受到延长肋位的影响,易造成声辐射模态形状及辐射效率的不准确。Peters等[12]则研究了采用边界元方法得到的不对称阻抗矩阵对三维结构声辐射模态的影响。吴海军等[13]使用快速多极子边界元方法分析了简支板的声辐射模态,主要的贡献在于提高运算速度和减小内存占用,为利用快速多极子边界元方法深入研究三维结构的声辐射模态奠定基础,但也指出[14],对于任意复杂结构,此方法输出一组非最有效的声辐射模态,因此不适合任意复杂结构的声辐射模态的求解。上述方法都是通过结构表面振速和结构表面声压获得辐射算子,进而获得声辐射模态。
吴卫国等人[15]则研究了简支板声辐射模态的远场获取方法,但不能够在远场计算任意复杂结构的声辐射模态,因此本文借助声传递矩阵(Acoustic Transfer Matrix,简称ATM)提出一种适用于任意复杂结构的远场声辐射模态求解方法,并分析了不同的场点形状、不同的场点距离及不同的场点数目对获取的声辐射模态的影响。
1 声辐射模态理论
1.1 结构的辐射声功率定义
任意复杂结构的辐射声功率P可由结构表面声压ps和表面法向振速vs表示[4]为

或由场点声压pf表示[4]为

式中Γ为结构表面,Ω为场点构成的曲面,()*表示()的复共轭,Re{}表示取实部,y为结构表面上一点,x为流体中一点。
1.2 BEM中结构表面声压和表面振速的表示
根据BEM可知,在辐射问题中,结构表面声压ps和结构表面法向振速vs满足

其中矩阵As和Bs分别由边界元积分核函数确定,称之为边界元系数矩阵,i为虚数,k为波数,z0=ρ0c0,为流体的特性阻抗,ρ0为流体密度,c0为流体中声速,Z称为声辐射阻抗矩阵。
将式(3)带入式(1),并离散化可得

1.3 声辐射模态及其辐射效率
对C进行特征值分解(Eigenvalue Decomposition,即EVD),有

其中若采用常单元进行计算,节点数目和单元数目相等,均为N,则Q为N×N阶实矩阵,由N个N阶特征向量qk(k=1,2,...,N)组成,Λ为特征值λk(k=1,2,...,N)构成的对角矩阵,qk表示一种可能的速度分布,代表了一种固有的辐射形式,即第k阶声辐射模态(Acoustic Radiation Mode,即ARM),第k阶声辐射模态的辐射效率定义[4,5]为

因上述的求解基于结构表面声压和结构表面法向振速求解,本文将此声辐射模态求解方法命名为ARM-SS(ARM on Structrue Surface)。
2 声辐射模态远场计算方法
任意结构声辐射在场点引起的声压,根据BEM有

令
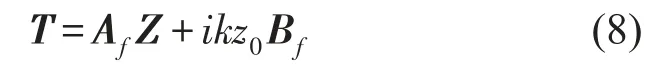
有

其中矩阵Af和Bf分别由边界元积分核函数确定,称之为边界元系数矩阵,T称为声传递向量(Acoustic Transfer Vector,即ATV,适用于单个场点)或声传递矩阵(Acoustic Transfer Matrix,即ATM,适用于多个场点),建立了辐射问题中场点声压与结构表面法向振速之间的映射关系。
同时注意到式(8)建立了矩阵T与声辐射阻抗矩阵Z之间的映射关系,而通过式(4)可知耦合矩阵C可通过声辐射阻抗矩阵Z获得,因此可通过声传递矩阵T计算耦合矩阵C。
在取多个场点时,T矩阵大小为Nf×N维,表示结构上每个小单元的法向振速与场点球面Ω上每个小单元声压之间的关系。一般地,场点单元数目Nf与结构单元数目N并不相等,因此矩阵T为长方形矩阵,不是方阵。
将式(2)离散化,可得

其中矩阵F为一对角矩阵,若用SΩi表示场点球面Ω上第i个小单元的面积,则

因此其大小为Nf×Nf维。
将式(9)代入式(10),有

若定义

则式(2)与式(4)最右端相等,且矩阵C大小为N×N维,可对式(13)中矩阵C进行如式(5)和式(6)的声辐射模态相关求解。
此方法计算耦合矩阵C所需矩阵T和F均为场点的相关参量,不需要在结构表面进行求解,因此属远场方法;同时,本方法基于声传递矩阵T进行计算,因此,将其称为ARM-ATM(ARM based on ATM)。另外声传递矩阵T可针对任意复杂结构体进行计算,因此本方法适合任意复杂结构体的声辐射模态求解,且可通过商业软件SYSNOISE或LMS Virtual Lab等获得,一旦声传递矩阵和场点面积对角矩阵获得,则结构的声辐射模态便可通过计算得到。
3 性能分析
由于脉动球辐射声功率具有理论解,为了验证ARM-ATM的正确性,选取半径a=1 m的脉动球壳进行验证。使用四边形映射网格划分为2 402个节点和2 400个单元。流体为水,其密度ρ0=1 000 kg/m3和声速c0=1 500 m/s,分别采用不同的场点形状、不同场点距离、不同场点数目,研究其对所获得的结构辐射声功率、声辐射模态形状、各阶声辐射模态效率的影响。
3.1 不同场点形状的影响
采用两种不同场点包络形状进行计算,球形包络和椭球形包络,其中:球面场点半径10 m,包含602个节点、600个单元;椭球场点由球面场点分别对x、y、z坐标放大1、1.5、2倍得到,同样包含602个节点、600个单元。
(1)辐射声功率:利用所获得的声辐射模态对脉动球不同波数下的辐射声功率进行计算,其相对误差及所需声辐射模态数目如表1所示。
可见,由ARM-SS和ARM-ATM方法获得的辐射声功率相对误差均在合理范围内,且相对误差随波数的增加而增大。椭球场点的相对误差比球状场点误差大约1%,其原因可归结为椭球包络与球状结构网格产生的一定程度的失配。对ARM-SS和ARM-ATM,两种方法在小波数下重新计算辐射声功率所需模态数目均为1,随着波数的增加,所需模态数目显著增加,且ARM-SS和ARM-ATM方法所需模态数目几乎一致。
(2)声辐射模态幅值:所获得声辐射模态形状,除第1阶模态外,与文献[5]具有极高的相似性,表2给出了k=0.1时第1阶模态的平均值、最大值及最小值比较。可见,通过ARM-SS和ARM-ATM方法获得的第1阶ARM的均值几乎相同,而无论对球形场点还是对椭球场点,ARM-ATM方法获得的最大值比ARM-SS方法稍大,但最小值却比ARM-SS方法小得多,其原因归结为场点网格面积的影响,且仅有四个单元的幅值为此最小值,大多数单元幅值等于或接近最大值。因此,ARM-ATM方法对声辐射模态形状影响不大。

表1 采用ARM-SS和ARM-ATM方法计算辐射声功率所需模态数目及对应相对误差
(3)声辐射模态辐射效率:两种方法在k=0.1和k=12时的各阶模态辐射效率比较如图1所示。
由图1(a)可见,在小波数情况下,根据ARM-SS和ARM-ATM方法获得的声辐射模态辐射效率具有如文献[5]所述明显的分组特性。同时,注意到其数量级,从第2阶模态开始,ARM-ATM方法获得的辐射效率比ARM-SS稍大,而球状场点的比椭球场点的稍大。但根据表1可知,在小波数情况下,辐射声功率的计算仅需要第1阶模态,因此对辐射声功率的计算不产生影响。

表2 k=0.1时第1阶模态平均值、最大值及最小值比较

图1 ARM-ATM与ARM-SS对辐射效率影响情况比较
由图1(b)可见,在较大波数情况下,对于中低阶模态而言,ARM-SS对应的辐射效率几乎不变,但ARM-ATM对应的辐射效率随着模态阶数有较小的变化,易见球状场点对应的辐射效率具有明显的分组特性,其原因为引入的场点对其产生了一定的影响。同时,ARM-ATM获得的辐射效率比ARM-SS获得的辐射效率稍大,从而解释了表1中椭球场点k=12和k=16所需模态数目稍少的原因。随着模态阶次的增加,不同方法间的辐射效率差异逐渐减小。
综上,不同场点包络形状对结构辐射声功率的计算及声辐射模态的获取影响不大。
3.2 不同场点距离的影响
为了研究场点在不同距离处对ARM-ATM的影响,3.1节中的球形场点被缩小或放大为半径R分别等于1.01 m、2 m、10 m、100 m和1 000 m的球形场点,其节点数目和单元数目仍然分别为602和600个。显然半径为1.01 m和2 m属于近场场点,而剩余三个为远场场点。
(1)辐射声功率:不同半径场点计算得到的辐射声功率相对误差及所需模态数目如表3所示,限于篇幅所限,将半径10 m和100 m的相应数据省略掉,其相对误差及所需模态数目均与1 000 m对应数据相同。可见,对辐射声功率的相对误差而言,不同半径的场点包络没有明显的区别,且辐射声功率相对误差均在合理范围之内。然而,在波数较大时,近场场点所需模态数目较远场场点要多,而此情况对R=1.01 m更甚,其原因在本节(3)中进行讨论。但远场场点则不受此影响,远场场点所需模态数目保持了良好的一致性。
(2)声辐射模态幅值:在3.1节已经对半径为10 m的球状场点和ARM-SS方法进行了比较,因此,本节将k=0.1时半径为10 m的球状场点所获得的前9阶声辐射模态作为基础进行比较。研究发现:对半径1 000 m的场点,第1阶模态的最大值、最小值与半径10 m处的相对误差达到了10-4的数量级,而第2阶—第8阶模态也保持在10-2的数量级,仅第9阶模态的相对误差稍大,但仍在正常范围内。尽管半径2 m的相对误差比半径1 000 m的误差稍大,但结果仍然可信。而由半径1.01 m场点计算的第1阶模态最小值误差相当的大,但其原因在3.1节(2)中已进行了讨论。同时第8阶及第9阶模态误差也相当大,但在计算辐射声功率时仅需第1阶模态,因此,不同场点位置对基于ARM-ATM计算的结构辐射声功率影响甚小。
(3)声辐射模态辐射效率:图2给出了不同场点距离处获得的声辐射模态辐射效率的比较,可见,R=1.01 m对应的辐射效率在小波数及大波数情况下均较其他距离处大。
在波数较小情况下,半径1 000 m场点和100 m场点对应的辐射效率完全重合,且从第2阶模态开始,同阶模态辐射效率随场点距离减小有所增大,但在小波数情况下,计算辐射声功率时仅需第1阶模态,因此对辐射声功率的计算没有影响。
在大波数情况下,除半径为1.01 m场点对应的辐射效率曲线,其他半径场点辐射效率曲线表现出了明显的聚类特性,这也就解释了表3中除R=1.01 m外,使用不同场点计算辐射声功率所需模态阶数大致相同的原因。需要注意的是,从理论上来说R= 1.01 m对应的辐射效率较大,则计算辐射功率理应需要更少模态数目,但从计算结果来看在频率稍高时,需要更多阶模态数目,其原因为:在R=1.01 m处求解,相当于在贴近结构表面计算,边界元计算过程中场点到单元的距离远小于单元特征长度导致的计算误差,不可避免地产生了大量近奇异积分,造成了积分结果的不准确,进而导致所获取的辐射模态幅值不准确。
因此,使用ARM-ATM计算结构的辐射声功率及声辐射模态,只要场点不紧贴结构表面,均可获得较理想的结果,而对于紧贴表面的测量与计算,采用ARM-SS则更经济、有效。
3.3 不同场点数目的影响
为了研究在不同场点数目对ARM-ATM的影响,3.1节中的球形场点分别被划分为24个、384个、600个及1 536个单元,用于验证其性能。
(1)辐射声功率:使用不同场点数目计算得到的辐射声功率相对误差及所需模态数目如表4所示,可见,使用单元数目较多的场点计算辐射声功率,从相对误差上来看没有明显的区别。但对于单元数目较少,如24个单元时,小波数和大波数对应的相对误差均较大,但仍在可容忍范围内,误差较大的原因归结为单元划分的粗糙程度,10 m的球形场点仅用24个单元进行表示,从图形上来看并不是球形,而是一个24面体,因此引入了较大的误差。但从大波数的分析来看,所需模态阶数有了大幅降低,因此其收敛性较好,即场点单元数目较少时适用于对测量误差要求不高的粗测。
(2)声辐射模态幅值:由于3.1节和3.2节已分别将半径R=10 m球状场点与ARM-SS和不同半径的球状场点进行了比较,本节将其作为基础进行对比,其单元数目为600个,研究发现:在球状场点单元划分数目不同时,除24个单元场点对应的第一阶模态的最小值以外(其原因在3.1节已进行过讨论),利用ARM-ATM方法获得的前7阶声辐射模态差异很小,而第8、9阶模态则差异较大,但在k=0.1等小波数情况下计算辐射声功率时仅与第1阶模态有关,因此对辐射声功率的计算影响很小。同时注意到,场点数目稍大会有利于声辐射模态的准确获取,其原因可理解为场点数目较多时,场点接受的信息冗余度增加,有助于信息的准确获取。

表4 采用不同场点数目时ARM-ATM方法计算辐射声功率所需模态数目及对应相对误差
(3)声辐射模态辐射效率:不同场点数目对辐射效率的影响如图3所示。可见,在小波数情况下4种场点划分方法获得的辐射效率具有很高的吻合度。但在大波数情况下,对辐射效率曲线而言,使用场点数目较少的单元划分方法大于场点数目较多的单元划分方法,如图3(b)所示,384个单元、600个单元及1 536个单元划分方法的辐射效率保持了较高的一致性,但24单元划分方法的辐射效率比前三者均高,解释了表4中24个单元划分方法用于求解辐射声功率所需模态数目少、收敛性好的原因。
因此,单元数目较多时对于声辐射模态的获取及辐射声功率的计算影响很小,而单元数目较少时适合测量要求不高的粗测。需要说明的是:高波数情形下远场声压变化比低波数情形要复杂,因此要获得足够准确的声场数据计算声辐射模态,就需要布置更多的场点,需要考虑声波的空间分辨率因素,即采样空间分辨率要满足声波的空间采样定律。

图3 不同场点数目对辐射效率的影响比较
4 结语
借助声传递矩阵将结构表面振速和场点声压联系起来的特性,将声传递矩阵引入到声辐射模态的求解当中,使在远场计算任意复杂结构的声辐射模态成为可能,给出了远场计算任意复杂结构体的声辐射模态的通用方法ARM-ATM,利用脉动球辐射声功率及声辐射模态幅值及效率进行性能验证,通过不同的场点包络形状、不同的场点距离及不同的场点数目的比较,对其性能进行了分析。结果表明:只要场点不贴近结构表面,ARM-ATM方法在不同场点包络、不同场点距离处及不同场点数目下均可获取较可信的结果。
[1]Borgiotti G V.The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements[J].The Journal of the Acoustical Society of America,1990,88(4)∶1884-1893.
[2]Sarkissian A.Acoustic radiation from finite structures[J].The Journal of the Acoustical Society of America,1991, 90(1)∶574-578.
[3]Elliott S J,Johnson M E.Radiation modes and the active control of sound power[J].The Journal of the Acoustical Society ofAmerica,1993,94(4)∶2194-2204.
[4]Cunefare K A,Currey M N.On the exterior acoustic radiation modes of structures[J].The Journal of the Acoustical Society ofAmerica,1994,96(4)∶2302-2312.
[5]Cunefare K A,Currey M N,Johnson M E,et al.The radiation efficiency grouping of free-space acoustic radiation modes[J].The Journal of the Acoustical Society of America,2001,109(1)∶203-215.
[6]桑艳平,姜哲,韦庆杰.基于声辐射模态的有源解耦控制的溢出问题及控制模型[J].噪声与振动控制,2012,32 (3):99-103.
[7]姜哲.声辐射问题中的模态分析:I理论[J].声学学报,2004,29(04):373-378.
[8]黎胜,赵德有.结构声辐射的振动模态分析和声辐射模态分析研究[J].声学学报,2004,29(03):200-208.
[9]赵志高,黄其柏.复杂结构的声辐射解耦及其声辐射效率分析[J].振动工程学报,2004,17(03):78-83.
[10]沈火明,张波,支伟.基于非协调边界元法的声辐射模态分析[J].噪声与振动控制,2011,31(06):104-108.
[11]张晓宇,陈美霞,魏建辉.圆锥壳和圆柱壳声辐射模态特性比较[J].舰船科学技术,2012,34(08):7-11.
[12]Peters H,Kessissoglou N,Marburg S.Enforcing reciprocity in numerical analysis of acoustic radiation modes and sound power evaluation[J].Journal of Computational Acoustics,2012,20(03)∶1250005.
[13]Wu H,Jiang W,Liu Y.Analyzing acoustic radiation modes of baffled plates with a fast multipole boundary element method[J].Journal of Vibration and Acoustics, 2013,135(1)∶011007-011007.
[14]Wu H,Jiang W,Zhang Y,et al.A method to compute the radiated sound power based on mapped acoustic radiation modes[J].The Journal of the Acoustical Society ofAmerica,2014,135(2)∶679-692.
[15]吴卫国,王贵成,马利杰.基于远场方法的结构声辐射模态研究[J].应用基础与工程科学学报,2006,14(1):93-99.
Far Field ComputationApproach ofAcoustic Radiation Modes forArbitrary Structures
YU Hai-tao1,2,WANG Ying-min1,WANGQi1,GOU Yan-ni1
(1.School of Marine Science and Technology,Northwestern Polytechnical University, Xi’an 710072,China; (2.School of Science,Xi’an University of Science and Technology,Xi’an 710054,China)
∶Acoustic radiation modes(ARM)have achieved satisfactory effects in adaptive noise control.However,lack of effective and convenient measurement or computation approach hinders them from their further development.Since the acoustic radiation power at the far field enclosed envelope is equal to that in structure surface,the solution of ARM can be converted to the computation in fluid domain with the help of the concept of acoustic transfer matrix(ATM).In this paper,a general far field computation approach for arbitrary structures is proposed.To validate the feasibility of this approach,the performance of acoustic radiation power of structure,amplitudes of ARM and efficiency of ARM are analyzed with different shapes of field point envelope,different radius field point envelopes and different numbers of field points.As an example, the acoustic radiation power of a pulsing sphere is calculated by using the ARM obtained at the far field,and is compared with the theoretical solution.The computation results show that the different field point conditions have only a little influence on the computation of acoustic radiation power,and the obtained ARM and its efficiency have high credibility.The proposed approach has provided a theoretical basis for measurement ofARM at the far field.
∶acoustics;acoustic radiation mode;acoustic transfer matrix;boundary element method(BEM);radiation power;radiation efficiency
TB535< class="emphasis_bold">文献标识码:ADOI编码:
10.3969/j.issn.1006-1335.2014.06.001
1006-1355(2014)06-0001-06
2014-05-06
国家自然科学基金项目(51309191);西安科技大学培育基金项目(201137)
鱼海涛(1979-),男,陕西长武人,博士生,主要研究方向:水下物理场与信息感知。
E-mail∶haitaoyu@xust.edu.cn
王英民(1963-),男,博士生导师。

