基于经验模态分解的桥式起重机振动模态分析

施科益 宁波市特种设备检验研究院

大吨位桥式起重机运行环境复杂，起重载荷、外部激励等因素所产生的振动对起重机结构、承轨梁及厂房造成了破坏。采用有限元分析方法可以有效分析桥式起重机的固有频率，使起重机避开其在使用过程中的外部激振频率[1-2]。该方法在起重机设计时具有较强的指导意义，但由于其计算精度不足和起重机实际制造水平的影响，有限元分析对于在用、维修和改造的起重机的模态分析结果并不理想。

对于复杂的起重机械，其振动信号往往存在非平稳特性。一般的平稳信号处理方法就不能胜任了。利用经验模态分解(Empirical Mode Decomposition，EMD)方法进行桥式起重机的模态分析具有较好的效果。EMD是一种自适应的时频处理方法，特别适用于非线性、非平稳信号的分析处理[3]。以模态分析理论为基础，通过对桥式起重机振动特性研究及其振动响应EMD分析，提出基于EMD的桥式起重机振动模态分析方法，并进行了仿真与实验研究，验证其在桥式起重机模态分析中的有效性。

1 机械系统模态分析理论

对于机械系统的振动问题，需要采用多自由度系统的振动理论分析。一个具有n个自由度的机械系统，在任一瞬时的运动形态要用n个独立的广义坐标描述，系统的运动微分方程一般是n个相互耦合的二阶常微分方程组成的方程组。对n自由度的无阻尼系统而言，具有n个固有频率，当系统按其中任意一个固有频率作自由振动时，系统的运动是一种同步运动，称为主振动。系统作主振动时所具有的振动形态称为主振型，或称为主模态[4]。对于多自由度的振动分析，通常采取振型叠加法，即选取主坐标，将n自由度系统的振动视为n个单自由度系统振动的叠加。

根据牛顿第二定律，建立n自由度机械系统的固有振动方程：

式中：M——n阶质量矩阵；

K——n阶刚度矩阵。

根据振型叠加法，主振动可设为

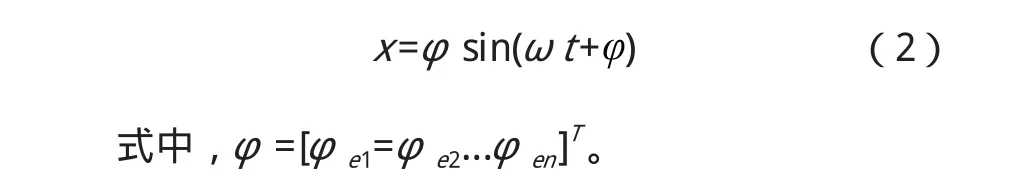
将式（2）代入式（1），根据正定系统的振动特点，可解得

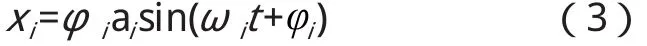
式中：φi称为第i阶主振型，也称作主模态；ai为常数；ωi为第i阶固有频率。

式（3）称为第i阶主振动模式。与固有频率一样，系统的主振型仅取决于系统的质量矩阵M、刚度矩阵K等物理参数。

当式（3）中i由1取到n时，就得到了系统的n个主振动模式，因此，n自由度系统的固有振动即为n个主振动模式的叠加，即

式(4)中，ai、为待定常数，由初始条件确定。

2 经验模态分解法

EMD方法的基本思想是将原始信号分解成一系列固有模式函数（Intrinsic Mode Function，IMF）的组合，然后根据实际需要，对各个IMF利用进行后续的处理分析。

EMD方法建立在以下的假设基础之上[3,5]：(1）信号至少有两个极值点，一个极大值和一个极小值；(2）特征时间尺度通过两个极值点之间的时间长度定义；(3）若信号数据缺乏极值点，但存在变形点，则可通过数据微分获得极值点，然后再通过积分来获得分解结果。一个IMF必须满足两个条件：(1）整个数据长度中极值点和过零点的数目必须相等或至多相差一个；(2）在任意数据点，局部极大值的包络和局部极小值的包络的均值须为零，即信号关于时间轴局部对称。

EMD的分解过程，可以描述如下[6]：

(1）确定信号x(t)的局部极大值和极小值，将所有极大值和极小值用三次样条插值函数插值形成数据的上下包络线，上下包络线的平均值记为m1(t)，求得：

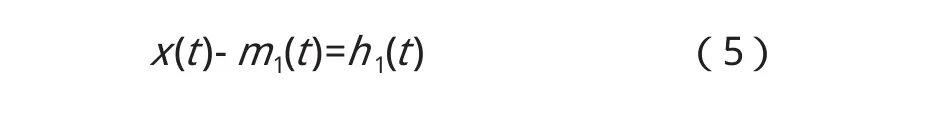
如果h1(t)是一个IMF，那么h1(t)就是x(t)的第一个分量；

(2）一般h1(t)不满足IMF条件，此时把h1(t)作为原始数据，重复步骤(1)，反复筛选k次，得到h1k(t)=h1k-1(t)-m1k(t)，使得h1k(t)满足IMF条件，记c1(t)=h1k(t)，称c1(t)为信号x(t)的第一阶IMF；

(3) 将c1(t)从x(t)分离出来，得到残余量r1(t)=x(t)-c1(t)，把r1(t)作为原始数据重复步骤(1)、(2)，从高频至低频可依次得到多阶固有模态分量ci(t)和残余量rn(t)。

整个过程遇到如下一个准则即终止：(1）分量cn(t)或残余量rn(t)足够小；(2）当残余量rn(t)作为一个单调函数不能再提取满足IMF时。最终原始信号x(t)可表示如下式：

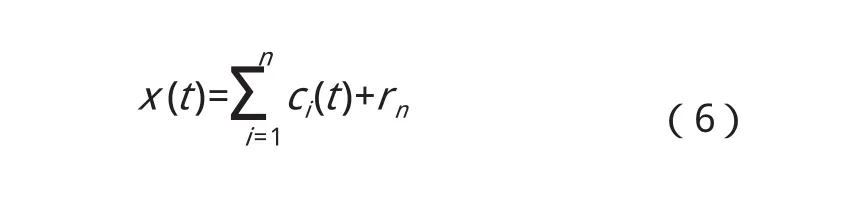
因此可以把任何一个信号x(t)分解成为n个IMF和一个残余量之和，固有模态分量分别包含了信号从高到低不同频率段的成分，且具有自适应性。

3 桥式起重机的EMD分析

以桥式起重机为对象，采用EMD方法进行振动模态分析。将桥式起重机简化为一匀质等截面的简支梁模型[7]，两端支撑限制垂直位移，一端同时限制水平位移，如图1所示。

图1 桥式起重机简化模型

以y=y(x,t)表示梁的振动位移，以ρ A表示梁单元长度的质量，EI为截面抗弯刚度，设梁上作用有单位长度的分布力F(x,t)，如图2所示。

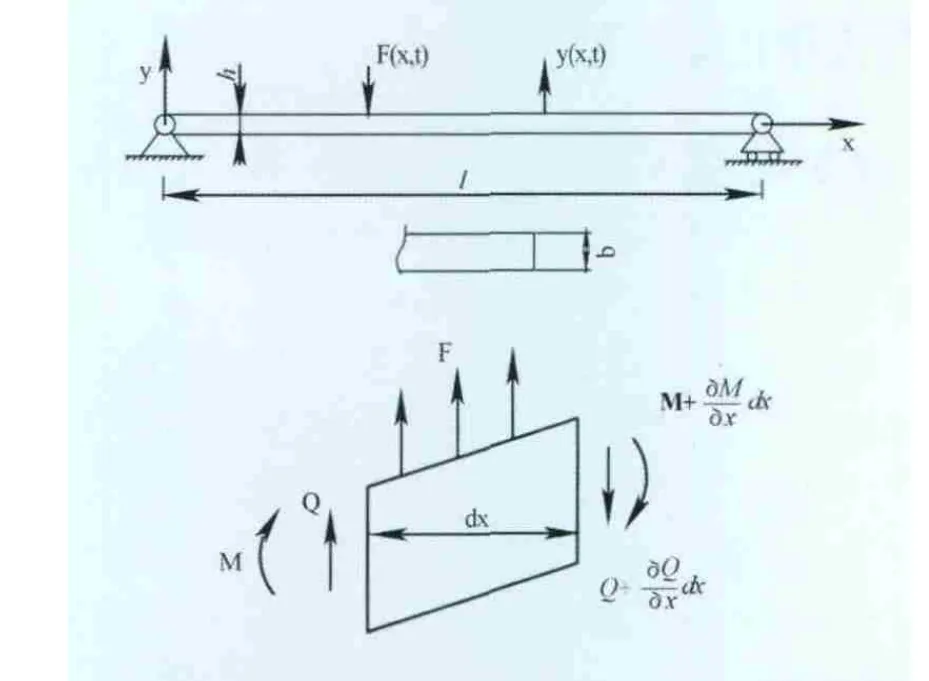
图2 简支梁振动模型

在梁的任意截面x处取一微段dx，其质量为ρAdx。受剪力Q(x,t)、弯矩M(x,t)和分布激扰力F(x,t)dx的作用。根据牛顿第二定律，在y方向的运动方程为：

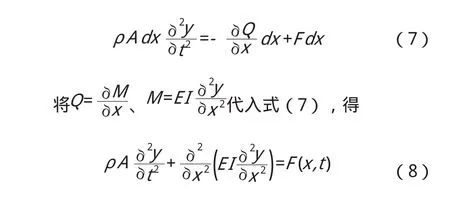
对于自由振动，设F(x,t)=0，求解系统各阶主振动为：

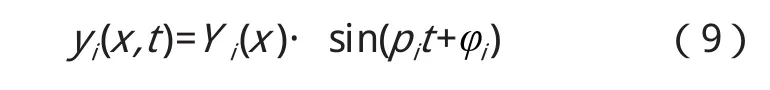
式中，Yi(x)为各阶振型函数。固有频率为：

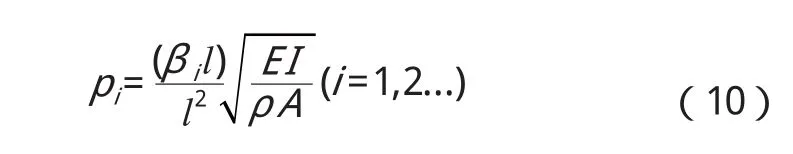
根据边界条件Y(0)=Y(l)=0,Y(0)=Y(l)=0,可求得 Yi(x)=Ci·sinβix，其中Ci为常数，βil=iπ(i=1,2...)。对于任意位置x0，其自由振动响应。

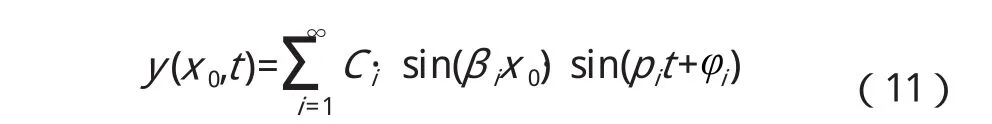
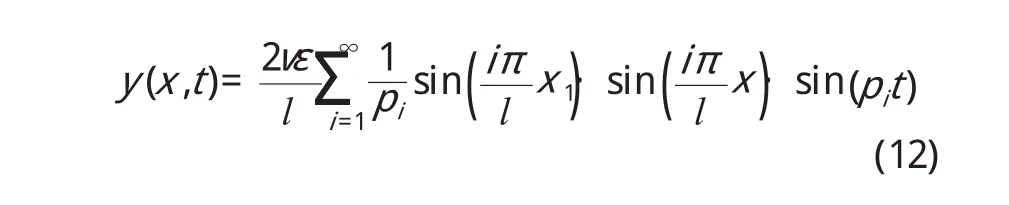
由于各阶振型的幅值与i2成反比，故会有低阶振型起主导作用，则在处的前三阶振动响应为：

对于式（13)，给定常数取值，其时域波形和各阶主振动模式分别见图3和图4所示。

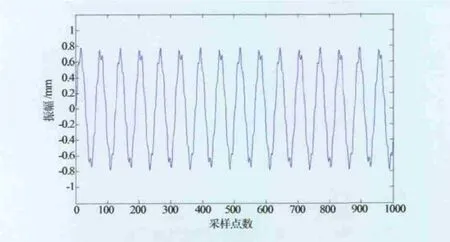
图3 简支梁振动响应时域波形

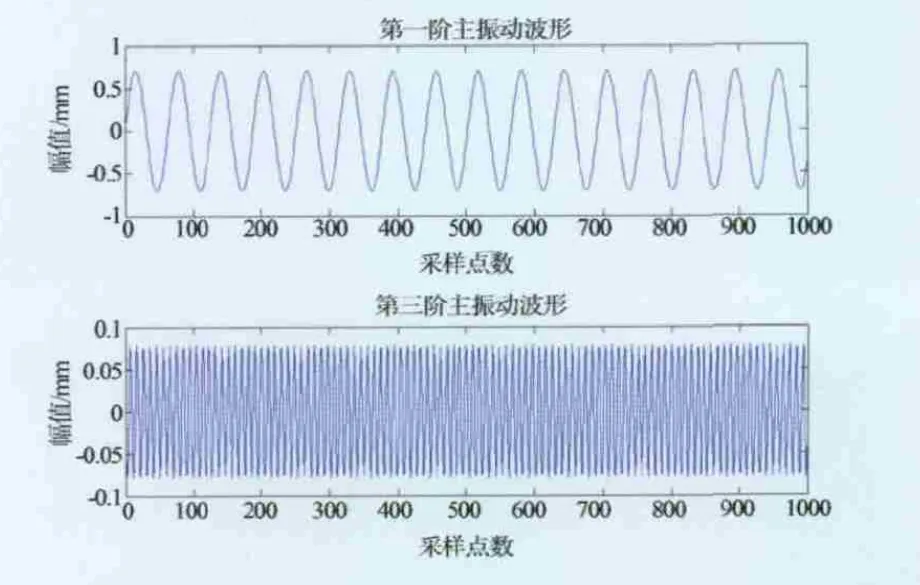
图4 主振动组成

对图3所示的简支梁振动响应进行EMD分解，结果如图5所示。

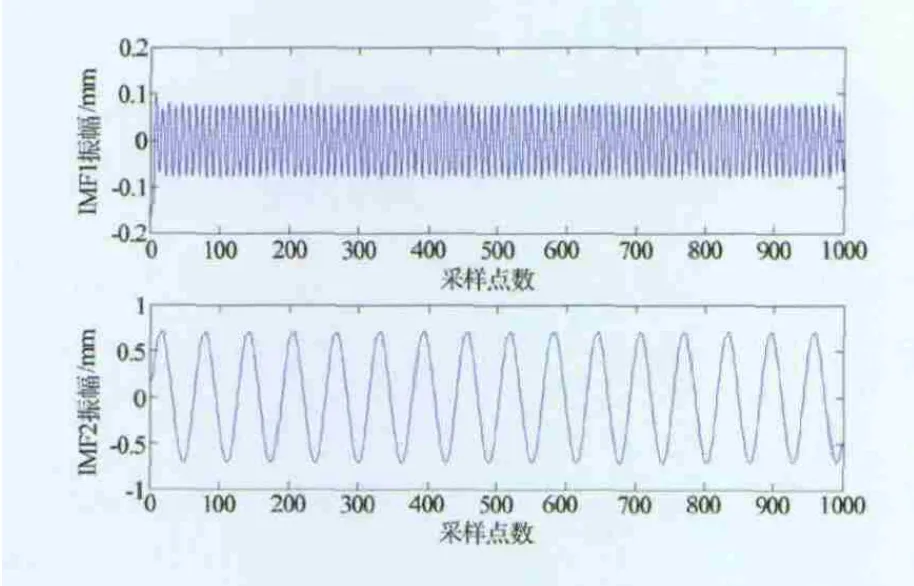
图5 EMD分解结果

对比分析图4和图5，可清晰地看出经EMD分解的得到的IMF1对应了第三阶主振动模式，IMF2对应了第一阶主振动模式，分解结果中并没有第二阶主振动模式，这也与理论分析结果相一致。计算IMF1与第三阶主振动模式和IMF2与第一阶主振动模式的误差及相关系数，结果分别见图6和表1。

图6 IMF与振动模式函数的误差曲线

表1 IMF与振动模式函数之间的相关系数

从图6中可见，固有模式函数与系统主振动模式函数之间的误差很小，远远小于振动幅值。且从表1中的相关系数可见，固有模式函数与系统主振动模式函数之间的相关性接近于1。这说明，简支梁的自由振动响应经EMD分解得到的固有模式函数与系统的主振动模式函数之间存在着物理对应关系。

4 简支梁振动实验

简支梁振动实验通过共振法激发简支梁的各阶振动模式，获得对应的振动信号，验证本文所提出的桥式起重机EMD模态分析方法的有效性。

如图7所示为简支梁振动实验装置的示意图。激振器激发简支梁振动，通过传感器采集振动信号进入PC机分析[8-9]。该简支梁参数为：l=60cm、b=5cm、h=0.8cm、E=2×105MPa。根据式（10）计算得到三阶振动固有频率分别为ω1=50.5Hz，ω2=201Hz，ω3=450Hz。

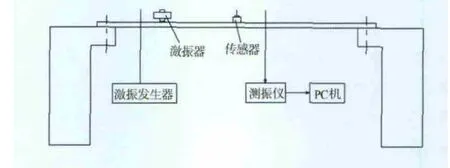
图7 实验装置示意图

调整激振频率，使得简支梁发生共振，测得一阶共振信号和二阶共振信号如图8、图9所示。将振动信号分别进行EMD分解，结果如图10、图11所示。

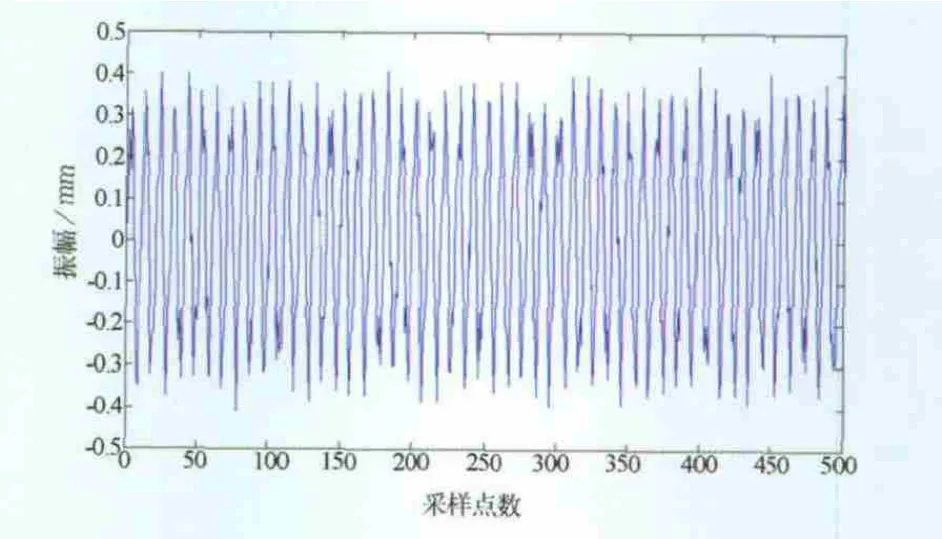
图8 一阶共振信号

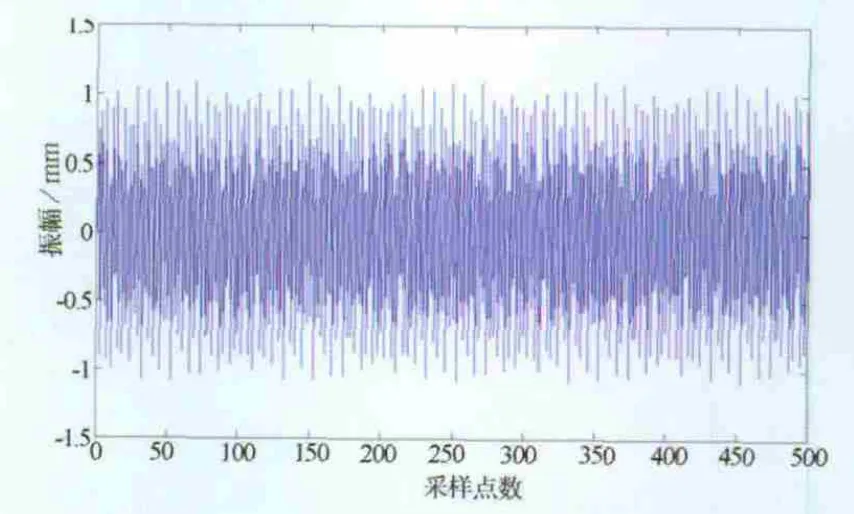
图9 二阶共振信号

图10 一阶共振信号EMD分解

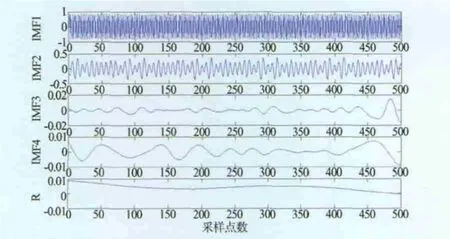
图11 二阶共振信号EMD分解

从图10、图11中可以看出IMF1与IMF2明显是系统振动模式。分别计算一阶、二阶的IMF1与IMF2的傅氏谱，结果如图12、图13所示。可见一阶和二阶共振频率包含于IMF1与IMF2的频率成分中，且与理论计算值也较为吻合。

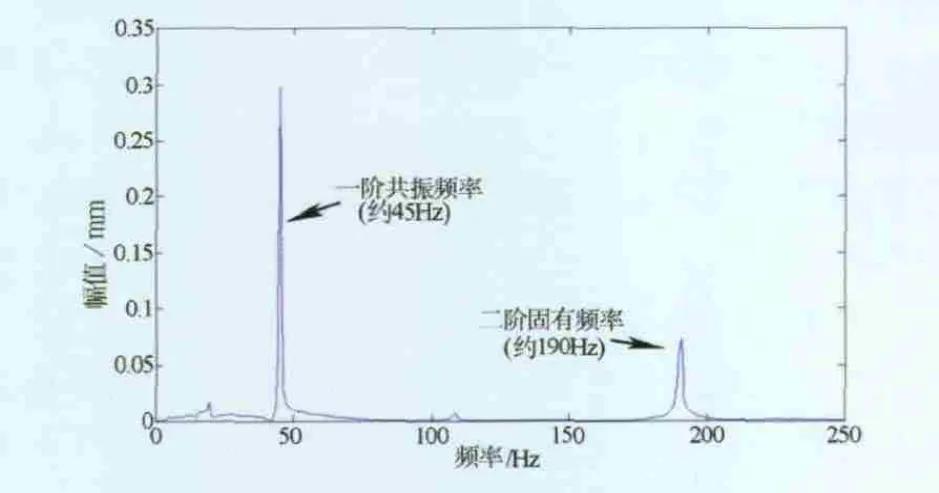
图12 一阶固有函数傅氏谱

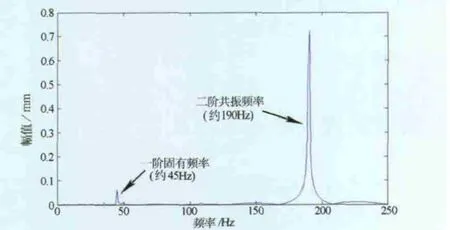
图13 二阶固有函数傅氏谱

实验结果表明简支梁振动信号经EMD分解得到的IMF和模态理论的振动模式之间保持较好的对应性，证实了桥式起重机EMD模态分析方法的可实现性。

5 结论

桥式起重机的振动模态分析是桥式起重机结构设计和制造的重要技术手段，将桥式起重机简化为简支梁模型，分析该模型的振动响应特性，应用EMD方法分析桥式起重机的振动信号，得到的IMF与振动模式之间有着高度的一致性。仿真分析与简支梁振动实验结果均表明基于EMD的桥式起重机振动模态分析是有效可靠的。

基于EMD的桥式起重机模态分析方法特别适用于在用、维修和改造的桥式起重机的模态分析，具有较高的分析准确性，为起重机的设计和安全运行提供参考依据。

1 杨明亮,徐格宁,常争艳,晋民杰.基于有限元法的桥式起重机桥架模态分析.机械科学与技术,2012,31(1):135－137

2 张学良,王家营,连晋华.基于ANSYS的桥式起重机主梁模态分析.起重运输机械,2007,(11):56－58

3 Norden E.Huang,S.Z.,Long SR.A new method for nonlinear and nonstationary time series analysis.4th international conference on stochastic structural dynamics,1999:559－564

4 李德葆,陆秋海.工程振动试验分析.北京:清华大学出版社有限公司,2004

5 Kejian Guo,Xingang Zhang.Application of EMD method to friction signal processing. Mechanical System and Signal Processing,2008,20(1):248－259

6 曹冲锋.基于EMD的机械振动分析与诊断方法研究.杭州:浙江大学,2009

7 J.D.Yau,Y.B.Yang.Vertical accelerations of simple beams due to successive loads traveling at resonant speeds.Journal of Sound and Vibration,2006,289,210－228

8 陈会莲,池丹丹,张明.机械设备状态监测虚拟仪器系统的研究.噪声与振动控制,2009,29(3):47－49

9 姜忠宇,赵转哲,毕海斌.简支梁振动实验台载荷识别的测试.试验技术与试验机,2007,47(3):26－29