虚拟试衣系统中的模型变形

杨晨晖，陈 辰

（厦门大学信息科学与技术学院，福建 厦门361005）

在虚拟试衣环境中，输入的数据都是通过摄像头等视频设备得到的二维图像或者图像序列.这些图像是仅有的包含了用户信息的数据，利用这些数据得到用户参数并生成个性化的三维人体模型的过程与基于图像建模的方法非常相似.基于图像的建模研究是使用二维图像生成或者修改三维模型，通过这样一种更自然的方式，使得三维建模的过程更加直观和高效.

根据建模过程中二维图像的不同种类，可以分为基于草图／手绘图的建模［1］和基于单张／多张图片的建模.其中基于草图／手绘图的建模主要关注通过用户使用笔型输入设备以传统绘图的方式构建三维模型，例如文献［2］中提到的利用手绘笔画对模型进行局部调整的方法，该方法能够快捷自然地修改模型，但是此方法需要人工标注模型轮廓线，且必须事先定义影响区域（ROI），操作复杂；文献［3－4］中介绍的草图建模方法使用了手绘线条的方式生成复杂模型，但是要使生成的模型准确，则需要绘制大量不同角度的线条来控制生成过程.基于单张／多张图片的建模目的在于从图像中重构出物体的三维模型，文献［5］中提出了一种从单张图片中生成三维模型的方法，但是生成的模型细节程度并不高；文献［6］使用了高斯过程隐变量模型方法从一组不同姿势的同一种物体的三维模型中训练得到人体模型姿势和体型的参数，并用来合成新的人体模型.

综合来说，基于草图的建模方法因其大量的交互操作并不能直接应用于虚拟试衣中，而基于图片的建模过程需要使用大量的同类模型作为训练集，而虚拟试衣中的人体模型是通过特殊的建模工具得到并绑定了衣物信息，难以得到同类的训练样本集.本文提出的变形算法通过均值坐标保存模型表面细节，使用人体轮廓图像与三维人体模型的匹配作为变形的约束，整个变形过程只需求解一个能量函数的最小二乘.无需任何人工交互，也不需要前期的预计算和学习过程.

1 虚拟试衣中的模型处理

在虚拟试衣系统中，我们使用工具制作身着衣物的人体模型，如图1（a）所示.这个人体模型被映射上用户的体型以及动作并在物理仿真阶段用作支撑衣物模型，但在渲染时并不被送入管线，所以最后用户只会看见衣物，如图1（b）所示.简单的说，人体模型就是用户的“替身”.为了使衣服能匹配用户体型，需要对人体模型进行变形，使其尽量能与用户体型对应.

2 三维模型变形方法流程

如图2所示，输入为原始三维网格模型M和二维轮廓图C，输出为新的网格M′.期间经过了模型编码、对应关系寻找、模型简化、模型变形和顶点恢复等阶段.

图1 用户模型替换人体模型Fig.1 The user′s body replace human model

图2 模型变形算法流程Fig.2 The process of model deformation

3 网格模型的编解码与轮廓点的匹配

3.1 网格模型编码与解码

本文使用一种基于均值坐标的形状编码对原始模型进行重新编码［7］.

锚点是网格上由用户指定的少数几个特殊顶点，通过移动锚点来控制整个网格的变形效果，如图3.

图3 原网格与变形后的网格Fig.3 Original model and twisting model

网格M由顶点集V和边集E组成.为了计算这个编码，使用这个顶点vi和它的邻接顶点vj1，…，vjm建立一个局部坐标系.其中vj1，…，vjm按顺时针排列.定义一个投影平面Pi：

其中平面的法线为ni＝（nx，ny，nz），di表示了从这些顶点到局部坐标系原点的平均距离.

均值编码中，每个顶点的编码包括两部分：正切部分wij和法线部分bij.其中正切部分是基于顶点在投影平面投影点，法线部分基于顶点对投影平面的距离偏移.

给定了这个投影平面后，将顶点vi和其邻接点vj都投影到此平面上：

最后得到

其中γij为角为角为‖v′

法线部分bij首先计算边（v′i，v′j）与法线ni的余弦值得到：

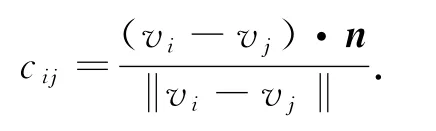
然后计算角度的余切值即该顶点编码的法线部分：

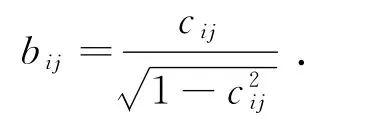
综上，得到了一个顶点均值编码的两部分：｛wij｜（i，j）∈E｝和｛bij｜（i，j）∈E｝.

通过顶点vi的均值编码和vi所有邻接顶点vj的坐标可以还原出vi的位置.根据文献［7］中的推导，vi可由以下解码公式得到：

其中Ni是一个3×3的矩阵：

在给出了单个顶点的解码方法后，对于整个网格，可以通过设置一个能量函数，并求解非线性最小二乘来得到变形后的网格：

其中V′＝V＼Va·Va表示网格中锚点的集合.

以上阐述了如何为网格编码，并通过解码得到变形后的网格.变形过程由网格上的锚点来控制，下面将说明如何得到锚点.

3.2 寻找轮廓点与三维模型匹配关系

在虚拟试衣系统中从外部输入设备提取用户人体轮廓作为人体三维模型变形的依据，将原始的人体三维模型变形为与用户体型相符的人体模型，为此必须将离散的二维轮廓点与三维网格模型的顶点对应起来，将这些对应后的网格顶点作为锚点向轮廓点移动以带动三维人体模型整体变形，如图4.本文使用基于隐马科夫链模型的笔画与模型匹配算法来建立人体轮廓与人体模型的对应关系.

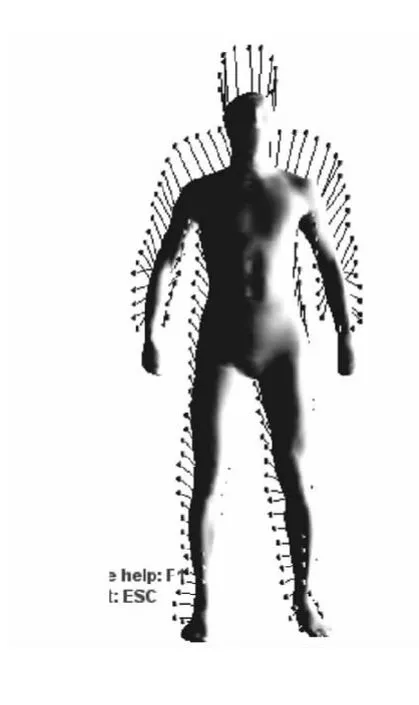
图4 轮廓点与模型顶点的对应关系Fig.4 The correspondence of outline and model′s vertex

3.2.1 局部相似性的量度

首先我们定义一些衡量的手段，使用两个量来界定轮廓点与模型顶点的性质：

其中np为轮廓点的法线，因为轮廓点在二维图像空间中建立时并没有法线信息，所以定义轮廓点的法线为np＝（（pi－pi－1）＋（pi＋1－pi）⊥（图5）.nv为三维模型顶点的法线.dp定义了一种轮廓点与模型顶点在距离上的量度，而dN从朝向上衡量点之间的相似性.

3.2.2 基于隐马科夫链模型的匹配

在给出了衡量轮廓与模型局部相似度方法之后，我们的目标就是求出使这些度量值的和最小的匹配.为了得到最优解，我们使用一种动态规划的方式来测试所有的匹配可能.这种动态规划解法建立在隐马科夫链模型的基础之上［8］.

在隐马科夫链模型中，输入是一组观察结果的状态序列，而目标是根据状态间的发散概率和转移概率找到一组最有可能产生这组观察序列的隐藏状态序列.在轮廓点与模型顶点匹配时，将轮廓顶点作为观察结果

图5 轮廓点的法线Fig.5 The normal of outline vertex

某组模型顶点序列作为隐藏状态

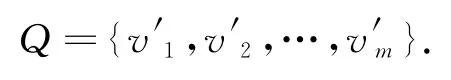
同时用局部相似性的量度定义发散概率和转移概率：

本文采用基于动态规划的Viterbi算法来求解.从第一个轮廓点p1开始，计算每一个隐藏状态vi产生当前的观察结果pj的概率P（pj｜vi），然后迭代计算在此基础上下一个隐藏状态vi＋1产生下一个观察结果pj＋1的概率P（vi＋1｜vi）×P（pj＋1｜vi＋1），最后回溯求得最优的隐藏状态序列.设ψc（i）为迭代至轮廓点pc，且状态序列为v′1，v′2，…，vi时产生观察结果p1，p2，…，pc的概率值；φc（i）则记录了迭代至pc且状态序列为v′1，v′2，…，vi时vi的前一个状态，记录了迭代的每一步并在最后用于回溯得到最优的状态序列.算法的步骤如下.

1）初始化：

ψ1（i）＝max1≤j≤nP（pj｜vi），1≤i≤n

φ1（i）＝0

2）迭代：

ψc（i）＝max1≤j≤n（ψc－1（j）P（pc｜vi）），1≤i≤n，2≤c≤m

φc

3）回溯：

由于模型顶点的数量可能非常巨大，在算法中需要直接过滤那些发射概率小于某个阈值的模型顶点，防止循环次数过多.而算法最后得到的轮廓点与模型顶点的匹配可能出现多对一的情况，因此在结束算法前还需进行后处理，根据发射概率将多对一简化为一对一.例如：p2和p3同时匹配到了v1，这时需比较v1对p2和v1对p3的发射概率，假设对p2发射概率为0.5而对p3概率为0.4，则选取概率值高的p2作为与v1的匹配轮廓点，剔除p3.造成多对一匹配的原因是网格顶点密度与轮廓点密度不相称，轮廓点的密度过大，所以此时并不需要将所有的轮廓点都匹配到模型顶点之上，而是将多余的轮廓点剔除.回溯之后得到的模型顶点序列v′1，v′2，…，v′m就是与轮廓点序列匹配的最优结果，如图6.

图6 匹配结果（局部）Fig.6 The result of match（partial）

4 网格模型简化

解码实际上是对一个非线性最小二乘问题进行求解，其解空间的维度为3×模型的顶点数，当需要变形的人体模型顶点数为1 000时，求解过程中使用的雅克比矩阵就高达上万维，直接导致算法效率低下.为了使解码过程更有效率，本文采用一种类似于文献［7］中使用的层次编码技术在编解码过程中引入网格简化操作，大幅减少解码阶段求解非线性最小二乘问题的规模.

4.1 三维模型的网格简化

在建立轮廓点与模型顶点的匹配后，得到V′＝｛v′1，v′2，…，v′m｝为网格上与轮廓匹配的顶点，同时也是控制整个网格变形用的锚点，¯V＝V－V′为非锚顶点.然后通过移除部分非锚顶点生成一个简化的网格.本文中使用了一种较为简单的网格简化方法，该方法基于文献［9］的顶点移除网格简化算法.流程如下.

1）计算顶点误差Ev＝｛ei，e2，…，en｝，

2）移除顶点vi，其中i＝argmaxi（Ev），

3）更新网格三角布局，更新vi邻接点的误差值，

4）如果maxi（Ev）或者‖Ev‖小于某个阈值时，则结束，否则执行步骤2）.

顶点的误差值代表了移除这个顶点之后的新网格与原网格的误差大小，而误差值可以根据顶点包含的局部细节程度定义，某个顶点越“尖锐”则其包含的细节程度越高，移除该顶点后造成的网格几何信息的损失也越大.每次移除时都选择误差值最小的顶点，以此在简化过程中保持模型的几何特征.如文献［10］中所提到的，可以根据顶点与其邻接三角面的平均距离计算该顶点的误差值，通过为每个顶点计算一个误差矩阵，可以很快地从某个顶点与其邻接顶点的误差矩阵中得到顶点误差值.具体的计算过程见文献［10］.

4.2 网格变形过程的改进

在通过移除顶点的方式来简化网格的同时，每次移除操作之前先计算该顶点的均值编码并储存起来.移除的模型顶点为Vr＝｛Vr1，Vr2，…，Vrn｝∈¯V，最后剩余的顶点为¯V∪V′，包括小部分非锚顶点和全部的锚点，且‖¯V∪V′‖＜‖V‖，简化后的网格模型为M′.然后对网格M′编码解码，其中解码过程由于简化了大量的顶点，因此计算速度得以提升.加入网格简化之后的模型变形详细流程如图7.

图7 结合网格简化的变形流程Fig.7 The deformation process with simplified mesh

在变形过程中加入模型简化操作，虽然使得编码过程需要更多的时间，但是大大加快了解码时计算非线性最小二乘优化的速度，且对于每个模型，只需要进行一次编码并保存均值编码和顶点移除的顺序，每次变形均可使用，这样整体变形过程将大大加快.

5 实验结果

本实验使用Visual Studio 2008软件环境，运行平台硬件环境为Pentium（R）Dual－Core 3.20GHz／DDR2 2.0G／Intel G41集成显示芯片组.实验结果如图8～10.对于球体模型，通过均值编码配合模型简化，最终能够很好得到纺锤状的三维模型，并保持了球体特征；而对于人体模型，使用变形算法生成了不同体型的模型.图10展示了不同身材的人穿着绿色衣服的效果.表1分别对比了球体与人体模型在未使用简化操作和使用简化操作的情况下变形算法执行情况，可以发现使用了简化操作之后算法效率大大提高.

图8 原模型的网格经过简化以及变形Fig.8 The mesh of original model have been simplified and deformed

图9 对人体模型变形后得到的不同体型的人体模型Fig.9 Different shape model of human body after deformation

6 讨 论

图10 不同身材的人试穿同款衣服Fig.10 Different men wear the same clothes

表1 网格变形算法结果Tab.1 The result of mesh deformation

本文介绍了三维网格变形的过程以及其在虚拟试衣中的应用.首先描述了网格模型的编码与解码，然后建立轮廓点与模型点的匹配关系，并利用轮廓点控制网格的变形，最后通过网格简化操作提高变形算法的效率.

在以后的工作中，我们将提高模型变形的精度，并将此模型变形算法应用到其他领域.

［1］Olsen L，Samavati F F，Sousa M C，et al.Sketch－based modeling：a survey［J］.Computers＆Graphics，2009，33（1）：85－103.

［2］Nealen A，Sorkine O，Alexa M，et al.A sketch－based interface for detail－preserving mesh editing［C］∥ACM Siggraph 2007Courses.New York：ACM，2007：42.

［3］Cherlin J J，Samavati F，Sousa M C，et al.Sketch－based modeling with few strokes［C］∥Proceedings of the 21st Spring Conference on Computer Graphics.New York：ACM，2005：137－145.

［4］Schmidt R，Wyvill B，Sousa M C，et al.shapeshop：sketchbased solid modeling with blobtrees［C］∥ACM Siggraph 2006Courses.New York：ACM，2006：14.

［5］Cashman T，Fitzgibbon A.What shape are dolphins？Building 3Dmorphable models from 2Dimages［J］.IEEE Trans Pattern Anal Mach Intell，2013，35（1）：232－244.

［6］Chen Y，Kim T K，Cipolla R.Inferring 3Dshapes and deformations from single views［C］∥Computer Vision—ECCV 2010.Berlin Heidelberg：Springer，2010：300－313.

［7］Kraevoy V，Sheffer A.Mean－value geometry encoding［J］.International Journal of Shape Modeling，2006，12（1）：29－46.

［8］Kobbelt L，Campagna S，Vorsatz J，et al.Interactive multi－resolution modeling on arbitrary meshes［C］∥Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM，1998：105－114.

［9］Botsch M，Kobbelt L.A remeshing approach to multiresolution modeling［C］∥Proceedings of the 2004Eurographics／ACM Siggraph Symposium on Geometry Processing.New York：ACM，2004：185－192.

［10］Garland M，Heckbert P S.Surface simplification using quadric error metrics［C］∥Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM Press／Addison－Wesley Publishing Co，1997：209－216.