基于Sparse K－SVD学习字典的语音增强方法

黄 玲，李 琳，王 薇，易才钦，郭东辉

（厦门大学信息科学与技术学院，福建 厦门361005）

语音信号增强是指从带噪信号中获取有用的语音信号，抑制噪声干扰，提升语音自然度和清晰度，常用的语音增强方法有谱减法［1］、小波阈值法［2］、卡尔曼滤波法［3］等.近年来，基于信号稀疏表示的语音增强算法［4］也受到广泛关注.

基于冗余字典的信号稀疏表示方法最早由Mallat和Zhang提出，一个可压缩信号在某一空间上可用极少的观测样本信号以高概率重构.基于信号的稀疏表示进行信号压缩、图像增强、语音增强、人脸识别等信号处理［4－6］，已取得了较好的成果.稀疏表示方法主要分为两个部分，冗余字典的构建和目标函数的优化.Zhang等［7］通过实验证明，稀疏表示方法改善信号处理性能的关键在于冗余字典的构建.目前主要有2种字典构建方法：固定字典法和字典训练法［8－10］.但这两种方法训练出的字典前者对信号的自适应性不佳，后者结构松散，字典规模受限，且运算量大.

为了解决上述问题，Rubinstein等［11］提出了一种新的字典学习方法——Sparse K－SVD算法，对冗余字典D进一步进行稀疏分解，使用小波变换或离散余弦变换建立一个基字典B，并寻找一个稀疏表示系数矩阵A，使得D＝BA.Sparse K－SVD算法通过对字典的稀疏表示，使得字典D具有良好的自适应性，同时降低了字典构建的计算复杂度，能够得到一个结构紧密的字典，利于进行更高维度、更大规模信号的稀疏表示.

本文提出一种基于稀疏表示的语音增强算法，采用Sparse K－SVD算法训练自适应的冗余字典，再应用正交匹配追踪（OMP）算法进行稀疏编码来重构纯净语音.在主观质量和客观指标上，基于稀疏表示的语音增强方法（分别使用Sparse K－SVD算法和K－SVD算法训练字典）比传统语音增强方法（小波法、谱减法、改进谱减法）获得更优的性能.在字典训练时间方面进行分析发现，相对于K－SVD字典训练算法，Sparse KSVD算法大幅度提高了计算效率.

1 语音信号的稀疏表示原理

任意长度为N的一维离散语音信号Y∈RN，通过冗余字典D∈RN×K可稀疏表示为：

式中：α为信号的稀疏表示系数，为K×1的向量，dk为给定冗余字典D中的一个原子，αk为α向量中与dk相对应的值.语音信号的稀疏表示是从冗余字典中选择具有最佳线性组合的若干原子来表示信号，实际上是一种逼近过程.从稀疏逼近角度出发，希望在逼近残差达到最小的情况下得到α最稀疏的一个解.这等同于解决下述问题［12］：

式中：‖‖0是l0范数，即不为零的元素个数，表示Frobenius范数的平方.

考虑语音噪声为加性噪声，其带噪语音模型如下：

其中，Y为带噪语音，X为原始语音，n为噪声.根据式（2）从冗余字典D中选取最佳线性组合的若干原子来表示带噪信号Y，当逼近残差足够小时，利用式（2）求解的稀疏表示矩阵，通过重构的和原始信号X近似，从而把纯净信号从带噪语音中分离出来，实现整个语音信号的增强.对于一个冗余字典D，式（2）的求解是个稀疏分解的过程.本文采用正交匹配追踪（OMP）算法进行稀疏分解，从而减少迭代次数.

2 双重稀疏的字典训练算法——Sparse K－SVD

Sparse K－SVD算法是在K－SVD算法的基础上，将字典D中原子由基字典稀疏表示：D＝BA，其中B是基字典，A是字典稀疏表示的系数矩阵.用Y，Γ分别为训练信号和训练信号的稀疏表示.从线性组合角度看，Sparse K－SVD算法是在式（2）的基础上，构建一个目标函数，针对目标函数进行最优化求解.其目标函数可表示为［11］：

其中，αi，∂j分别是Γ和A的任意列向量，t，p分别是αi和∂j中非零元素的个数.

字典的更新是逐列进行的.首先，假设系数矩阵Γ和字典D都是固定的，将要更新字典的第k列为dk，令系数矩阵Γ的第k行为αk，dk＝B∂k，∂k为矩阵A的第k列，此时，式（4）中的惩罚项可表示为：

上式中，乘积BAΓ被分解成N个矩阵和.每次逐列更新字典时，式（5）中项是固定的，所剩的一项，也就是要处理的第k项B∂k0αk0.矩阵Ek0代表去掉原子dk的成分所造成的误差.直接更新∂k0和αk0，得到的更新后的αk0是满向量，使得更新后的αk0中非零元素的位置和数量和未更新前的位置和数量不同，会出现发散.为了解决此问题，仅保留αk0中的非零值.因此，目标函数变为：

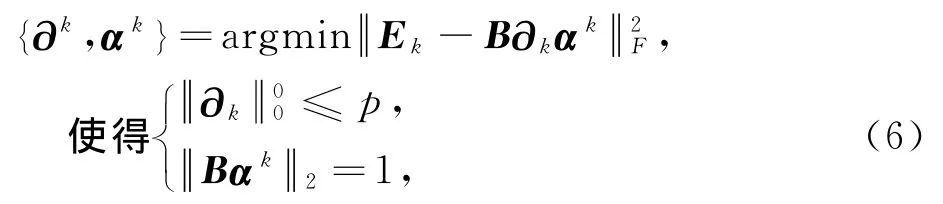
其中，Ek和αk分别是Ek0和αk0去掉零输入后收缩的结果.对于上式的第二个限制条件可在∂kαk保持不变时，通过调整∂k和αk的能量来满足.因此，式（6）可简化为；

接着优化αk：

从而式（7）可改写为：

式（10）与式（2）结构相似，Ekαk相当于式（2）中的Y，B相当于式（2）中的D.因此，问题变得更简单，方便计算.Sparse K－SVD算法完整的算法步骤如下所示：

输入：信号Y，基字典B，初始字典A.目标原子的稀疏度t，目标信号的稀疏度p，迭代次数L.

输出：字典的稀疏表示矩阵A，信号的稀疏表示矩阵Γ.

步骤：初始化：A＝A0

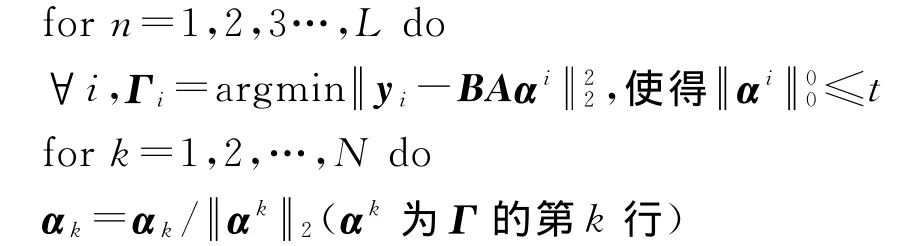
Ekαk＝（XI－BAΓI）αk（I为信号Y中用来表示αk的索引号）

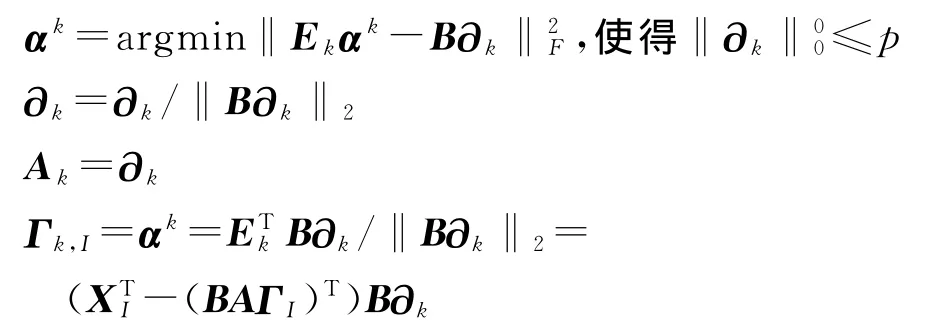
3 基于稀疏表示的语音增强方法

本文利用语音信号的稀疏性，进行语音增强处理，采用Sparse K－SVD算法训练冗余字典，式（2）可改写为：

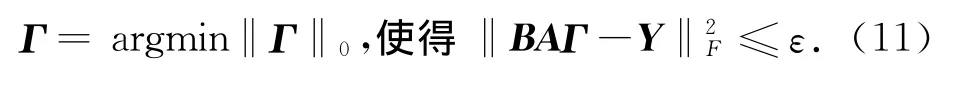
B是固定的基字典，很明显上式中有两个是未知的：字典的稀疏表示矩阵A和信号的稀疏表示矩阵Γ.

首先对带噪语音初始化，用冗余余弦字典初始化基字典B，用单位矩阵初始化A，利用OMP算法可以寻找到一个最优的Γ.然后，再通过Sparse K－SVD算法训练得到字典稀疏表示的系数矩阵A.不断迭代优化A和Γ，具体步骤如下所示：

1）初始化

对带噪语音进行分帧，帧长为N（如N＝128），同时构建一个冗余的余弦基字典B，这个基字典的大小为N×4N，A矩阵的初始值为单位矩阵.

2）稀疏编码

先假设BA是固定的，根据式（11）求解每帧信号稀疏系数矩阵.然后再利用OMP算法不断优化Γ，直到的值小于ε为止.

3）训练字典

每次更新A中的一个原子，在更新A的同时，也更新了信号稀疏表示的系数矩阵Γ.根据Sparse KSVD算法，用大量的帧长为M的语音训练字典系数A.由于A是字典D的稀疏表示系数，需要更新的原子数量相较于K－SVD算法大幅度减少.

4）语音重构

利用更新后的字典D＝BA和Γ，根据＾Y＝D＾α一帧一帧地重构原始语音信号.然后，对每帧重叠的部分采用均值化处理，从而实现整个语音信号的增强.

4 实验结果及分析

为了评价本文所提出的基于稀疏表示的语音信号增强方法的性能，本文对叠加高斯白噪声后，信噪比分别为－5，0，5，10，15dB的带噪语音进行主观质量和客观指标上的测试.本实验所用的原始语音文件来自NOIZEUS语音库［12］，下面实验除波形观察外，其他结果都是对NOIZEUS语音库里30个语音文件实验后所得的平均结果.实验的硬件平台为戴尔Inspiron1440型号PC机（2.2GHz主频），软件平台为MATLAB R2009b.本文所采用的基于Sparse K－SVD算法的语音增强方法和基于K－SVD算法的语音增强方法都是对带噪语音逐帧进行增强.每帧帧长128个样点，帧间重叠1个样点.K－SVD算法的初始字典是一个冗余的DCT字典，而在Sparse K－SVD算法中，也采用冗余的DCT字典作为基字典B，并把初始A矩阵设为单位矩阵.稀疏优化停止的条件是平均误差小于阈值ε.实验表明，当ε＝1.12σ时有更好的性能，这里的σ表示噪声的标准差.

4.1 主观质量的评价

随机选取NOIZEUS语音库中的一段语音“sp04.wav”，采样频率为8kHz，字长为16bit，其波形图如图1（a）所示.叠加信噪比为0dB的高斯白噪声，得到信噪比为0dB的带噪语音（图1（b））.采用不同方法进行语音增强后的波形图如图1所示.

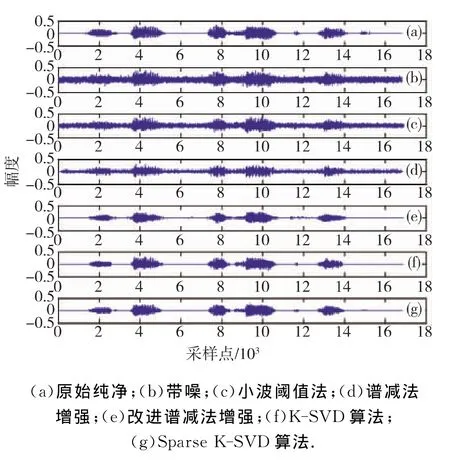
图1 sp04.wav的波形图Fig.1 Waveform of sp04.wav

由图1可知：1）被严重污染的带噪语音，经过基于稀疏表示的方法去噪后如图1（f）和（g）所示，噪声被大量消除，并且能很好地恢复原始语音的信息，而传统的语音增强方法（如图1（c）～（e）所示）去噪后还残留着许多未被消除的噪声；2）采用Sparse K－SVD算法的语音增强方法和采用K－SVD算法的一样有良好的降噪性能.另外，听音结果也显示基于稀疏表示的去噪结果能很好地分辨出原始语音信号，可懂度和清晰度均良好，而传统方法去噪结果的清晰度受到影响.

4.2 客观指标的评价

信号近似的准确率可以用重构误差ε来评价，它的定义如下式所示：

其中，s′（i）为增强语音的第i帧信号，s（i）为原始语音的第i帧信号.增强后的信号如果越接近原始信号，则ε的值越小.不同方法进行增强的重构误差如图2所示.从图2可知，当带噪语音的信噪比从－5dB变化到15 dB时，采用基于稀疏表示的增强方法（采用Sparse KSVD算法和采用KSVD算法）的重构误差很接近，都比传统增强方法的重构误差低.当叠加的噪声强度越大时，不同增强方法重构误差的差异就越明显.

图2 重构误差比较图Fig.2 Comparison of reconstruction error

本文还从信噪比和语音质量两个方面对不同增强方法的性能进行了对比，分别如表1和2所示.其中信噪比的定义如下：

表1 采用不同方法增强后信噪比的比较Tab.1 Output SNR for different enhancement methods dB

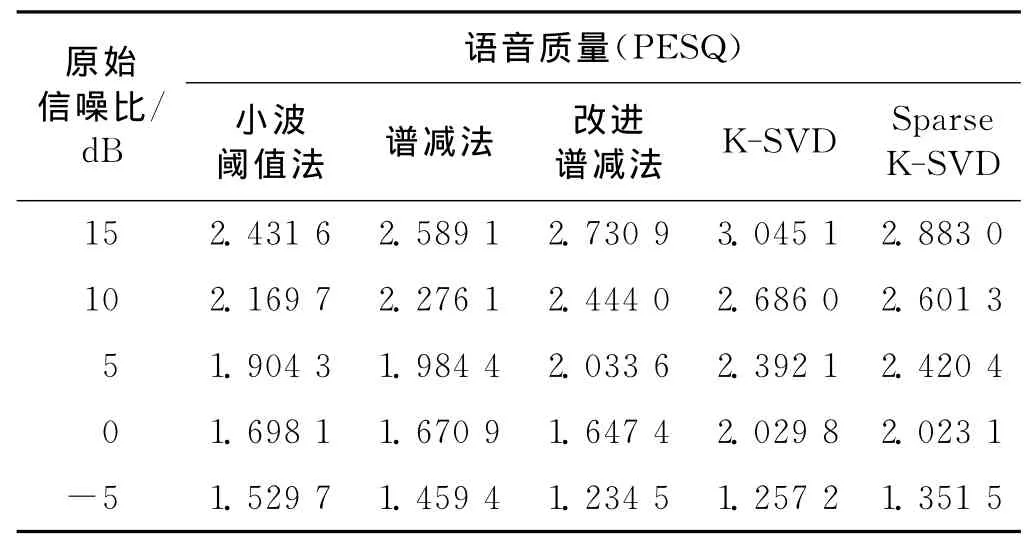
表2 采用不同方法增强后语音质量的比较Tab.2 PESQ scores for different enhancement methods

式中，s′（i）为增强语音的第i帧信号，s（i）为原始语音的第i帧信号.由表1可知，当带噪语音的原始信噪比从－5dB变化到15dB时，这几种增强方法在一定程度上都提高了信噪比和语音质量.不过，基于稀疏表示的增强算法（采用 K－SVD算法或Sparse K－SVD算法）的性能提高得更显著.

对采用不同字典训练算法（K－SVD和Sparse KSVD）的信号增强效果进行比较，基于Sparse K－SVD的稀疏表示法和基于K－SVD的稀疏表示法的增强性能不相上下.

4.3 语音增强方法计算时间的比较

对几种语音增强方法的计算时间进行了统计，如表3所示，可知，小波阈值法的计算时间最短，谱减法和改进谱减法的次之，而基于稀疏表示的语音增强方法（分别使用Sparse K－SVD算法和K－SVD算法训练字典）则消耗较长的时间.这是由于基于稀疏表示的语音增强方法训练大规模的字典（如字典原子数为512）耗时较长.由本文4.1节和4.2节的实验结果可知，在主观质量和客观指标上，采用Sparse K－SVD算法和K－SVD算法的语音增强性能都优于传统的语音增强方法.可见，语音增强处理中增强质量和计算时间是个权衡关系，需根据实际需求选择合适的语音增强方法.

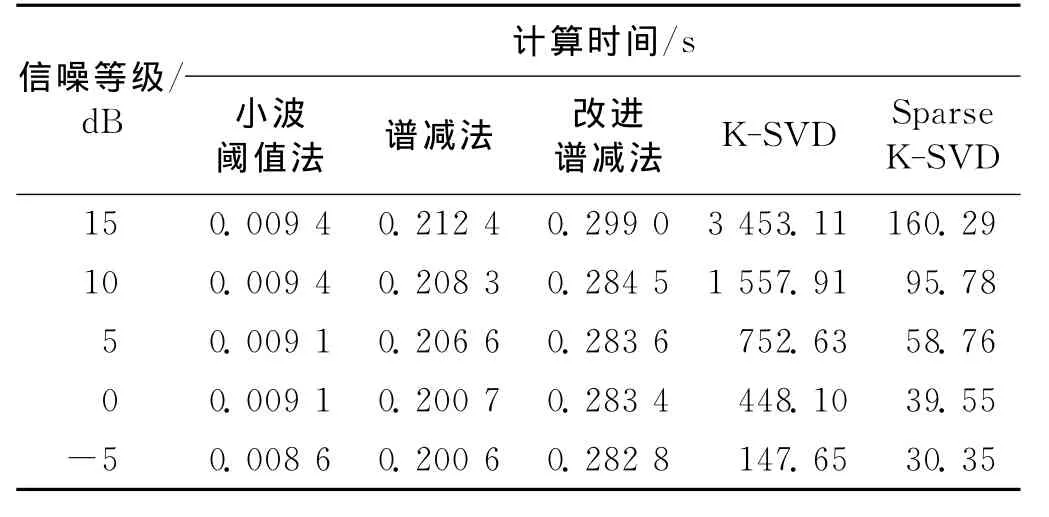
表3 语音增强方法计算时间的比较Tab.3 Time consumption for different enhancement methods

表3显示在相同噪声等级下，Sparse K－SVD算法训练字典的计算效率远高于K－SVD算法.尤其在15 dB噪声环境下，Sparse K－SVD算法的计算速度提高了二十几倍.可知，与K－SVD学习字典方法相比，基于Sparse K－SVD学习字典的语音增强算法能够在保证语音增强性能的前提下大幅度节省计算时间.

5 结 论

本文基于语音信号的稀疏表示理论，提出了一种采用Sparse K－SVD算法训练冗余字典的语音增强方法，不仅进一步优化了语音增强性能而且提高了计算效率.采用Sparse K－SVD算法训练出的字典结构紧凑，可用于处理大规模的语音数据.基于Sparse K－SVD的稀疏表示方法不仅可实现语音增强，还适合于其他的信号处理应用，如说话人识别、人脸识别、盲源分离等.

［1］Boll S.Suppression of acoustic noise in speech using spectral subtraction［J］.IEEE Transactions on Acoust，Speech，Signal Process，1979，27（2）：113－120.

［2］Vetterli M.Wavelets，approximation，and compression［J］.IEEE Signal Processing Magazine，2001，18：59－73.

［3］Paliwal K，Basu A.A speech enhancement method based on Kalman filtering［J］∥IEEE International Conference on A－coustics，Speech，and Signal Processing，1987，12：177－180.

［4］Zhao N，Xu X，Yang Y.Sparse representations for speech enhancement［J］.Chinese Journal of Electronics，2011，19（2）：268－272.

［5］Wright J，Yang A Y，Ganesh A，et al.Robust face recognition via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31：210－227.

［6］Elad M，Aharon M.Image denoising via sparse and redundant representations over learned dictionaries［J］.IEEE Transactions on Image Processing，2006，15：3736－3745.

［7］Zhang L，Yang M，Feng X C.Sparse representation or collaborative representation：which helps face recognition？［C］∥2011IEEE International Conference on Computer.Barcelona：IEEE，2011：471－478.

［8］Vidal R，Ma Y，Sastry S.Generalized principal component analysis（GPCA）［J］.IEEE Transactions on Image Process，2005，14（4）：423－438.

［9］Engan K，Aase S O，Hakon Husoy J.Method of optimal directions for frame design［C］∥IEEE International Conference on Acoustics，Speech，and Signal Processing.Phoenix，AZ：IEEE，1999，5：2443－2446.

［10］Aharon M，Elad M，Bruckstein A.K－SVD：design of dictionaries for sparse representation［C］∥Proc of the Workshop on Signal Processing with Adaptive Sparse Structured Representations（SPARS′05）.［S.l.］：SiteSeerX，2005：9－12.

［11］Rubinstein R，Zibulevsky M，Elad M.Double sparsity：learning sparse dictionaries for sparse signal approximation［J］.IEEE Transactions on Signal Processing，2010，58：1553－1564.

［12］Hu Y，Loizou P.Subjective comparison of speech enhancement algorithms［C］∥2006IEEE International Conference on Acoustics，Speech，and Signal Processing.Toulouse：IEEE，2006：153－156.