Friction Characteristics of Space Lubricating Oil No. 4129 in Rolling and Sliding Contact

Wang Yanshuang; Cao Jiawei; Li Hang; Li Pu; Yuan Qianqian

(Henan University of Science and Technology, Luoyang 471003)

Friction Characteristics of Space Lubricating Oil No. 4129 in Rolling and Sliding Contact

Wang Yanshuang; Cao Jiawei; Li Hang; Li Pu; Yuan Qianqian

(Henan University of Science and Technology, Luoyang 471003)

The friction coefficients between the surfaces of a ball and a disc lubricated by a space lubricating oil No.4129 were measured at various operating conditions on a ball-disc friction test rig. Friction characteristic curves were obtained under sliding and rolling movements at point contact. A new model for calculation of the friction coefficient was presented. The results show that the bigger the load is, the larger the friction coefficient becomes. The rolling speed ranging from 1 m/s to10 m/s has an important effect on the friction coefficient. The friction coefficient increases with the increase in sliding speed and the decrease in rolling speed. The linear variation region of the friction coefficient versus the sliding speed at high rolling speed is wider than that at low rolling speed. The model for calculation of the friction coefficient is accurate for engineering use.

lubricating oil; friction coefficient; rolling and sliding contact; friction characteristic

1 Introduction

The technologies for evaluating the performance of lubricating oils and greases include physicochemical performance evaluation and mechanical property evaluation. Physicochemical performance tests are quite mature technically. However, the mechanical performance tests are still not perfect. The mechanical properties of lubricants are mainly measured by means of the simulation test machine which is widely used for studying the friction characteristics of rolling bearings. The movement of the rolling elements relative to the raceway of a rolling bearing covers rolling and sliding. The rolling bearings are often in the regime of elastohydrodynamic lubrication. The routine friction and wear tester used widely in the present time, such as the four ball friction and wear tester, can only simulate the pure sliding movement and the boundary lubrication conditions. Jia Chao[1], Guo Feng[2]and Muraki[3]studied the variations in friction coefficient of a lubricating oil against the sliding speed and the load. There is a phenomenon which shows that although the properties of two different lubricants being measured in the routine friction and wear tester are similar, they could have great difference in practical applications. So the performance parameters which are obtained by the routine friction and wear tester cannot provide enough information for deciding if the lubricant can be adapted to the practical operating conditions. Pepper and Kingsbury developed a spiral trajectory friction meter[4-5], which can be used to measure the friction coefficient when the friction pair is in the state of rolling, sliding and spinning. However, it can only be used to measure the friction characteristics in the boundary lubrication regime. Lafountain[6]and Querlioz[7]studied the traction characteristics of several synthetic lubricants in the elastohydrodynamic lubrication condition. But these experiments can simply reflect the friction characteristics of the lubricants in the low rolling speed domain. The friction characteristics of an aviation lubricating oil in rolling/sliding contact were discussed in Refs.[8-10]

In this paper, the friction coefficients between the surfaces of a ball and a disc lubricated by a space lubricating oil No. 4129 were measured in broad operating conditions on a self-made friction test rig. The lubricating oil No. 4129 to be tested is suitable for lubricating the long-life and high-accuracy oil-impregnated bearings used in the gyro motor and the momentum wheel of the inertial navigationsystem in the aviation and space aircrafts. It is also applied to the high-precision bearings in other industrial sectors. The self-made friction test rig can simulate the actual working conditions of bearings and gears, and specifically it can be used to simulate the working conditions when the shear strain rate exceeds 106s-1. According to the experimental data, the variations in friction coefficient against the rolling speed, sliding speed and normal load were obtained. Meanwhile, a model for calculating the friction coefficient was established. The research results in this paper are important for the design of space bearings and the development of space lubricating oils.

2 Experimental

2.1 Test rig

The friction experiment was carried out on an improved ball-disc test rig which was designed and built by the Henan University of Science and Technology, as shown in Figure 1[11-12]. The test rig is made up of a ball specimen, a disc specimen, a power system, an oil feeding device of the loading system with a hydrostatic bearing, a test oil feeding system, a temperature controller, a cooling system, a friction measurement system, a normal load measurement system, and a data acquisition system.

The working principle of the ball-disc test rig is as follows: The ball and the disc are controlled by a horizontal Motor I and a vertical Motor II which are driven by two frequency changers. Various rolling speeds can be obtained by regulating the frequency changers. The load is applied to the rotating ball and the disc through a hydrostatic shaft which supports the Motor I. There is a load sensor under the hydrostatic shaft that can transmit the load to a deformeter. The test oil feeding system can spray the test oil into the contact region in order to develop a film with a certain thickness. The sliding speed, which is the speed difference between the disc and ball specimen, can be generated by adjusting the rotating speeds of the two motors. The sliding speed shears this oil film to create a friction force. The friction force makes the ball together with the Motor I rotate around the axis of the hydrostatic shaft to press the friction force sensor. The friction force can be picked up by the friction force sensor and the data acquisition system.

2.2 Experiment method

When the normal loadW, rolling speedU(U=(U1+U2)/2, whereU1andU2are the linear velocities on the surfaces of the ball and the disc specimens, respectively）and lubricant inlet temperatureTare adjusted to the specified values, the Motor I and the Motor II can be adjusted to obtain the different sliding speeds ΔU=U1-U2. The friction forceFcan be measured at each sliding speed ΔU. The curves in the form of the friction coefficient against the sliding speed for all the operating conditions can thereby be generated.

The following is the experimental conditions: 1) The range of the rolling speed is between 1 m/s and 20 m/s; and the rolling speed can be changed steplessly；2) The maximum Hertzian contact pressurep0ranges from 0.8 GPa to 1.5 GPa, and the corresponding normal loadWranges from 20 N to 135 N; 3) The lubricant inlet temperatureTis the ambient temperature (15 ℃); 4) Both the ball and disc are made of GCr15 steel and their average surface roughness is less than 0.02 µm. The diameter of the ball and the disc is 20 mm and 80 mm, respectively, with their surface hardness equating to HRC60—64.

Among the experimental conditions, the lowest speed is 1 m/s, and the maximum pressure is 1.5 GPa, while the computed minimum lambda ratio is 10.6＞3. It indicates that the surfaces of the friction pair are within the regime of the elastohydrodynamic lubrication.

2.3 The physical and chemical properties of the space lubricating oil No. 4129

The lubricating oil No. 4129 is mainly used in the precision bearings such as gyro motor and momentum wheel which are used in spacecraft, with its main charactersitics presented in Table 1.

Table 1 The charactersitics of lubricating oil No. 4129

Figure 1 Ball-disc test rig

2.4 Test results

The curves describing the friction coefficient versus the rolling speed can be obtained when the sliding speed ΔUis 0.04, 0.08, 0.12, and 0.19, respectively. Several representative test results are shown in Figures 2—4.

Figures 2—4 show that the friction coefficient of the No. 4129 space lubricating oil is very large when the rolling speed is 1 m/s. The friction coefficient decreases with the increase in rolling speed. When the rolling speed is in the range of 1 m/s—3 m/s, the friction coefficient decreases greatly with an increasing rolling speed. A subsequent increase in the rolling speed gives rise to a slow decrease in the friction coefficient which, at a certain point, reaches a critical value. A further increase in the rolling speed leads to a constant value or slight decrease in the friction coefficient. A higher rolling speed yielding a more heat can result in a viscosity decrease coupled with the increase in rolling speed. So the friction coefficient decreases with the increase in the rolling speed.

Figures 2—4 indicate that the rolling speed ranging from 1 m/s to 10 m/s has an important impact on the friction coefficient of the lubricating oil No. 4129. When the rolling speed surpasses 10 m/s, the friction coefficient keeps a constantly lower value with the increasing rolling speed. So the lubricating oil No. 4129 can adapt to the operating condition when the rolling speed exceeds 10 m/s.

Figure 2 Variation in friction coefficient (µ) with rolling speed (U) at different ΔU when P0=1.0 GPa , T=15 ℃

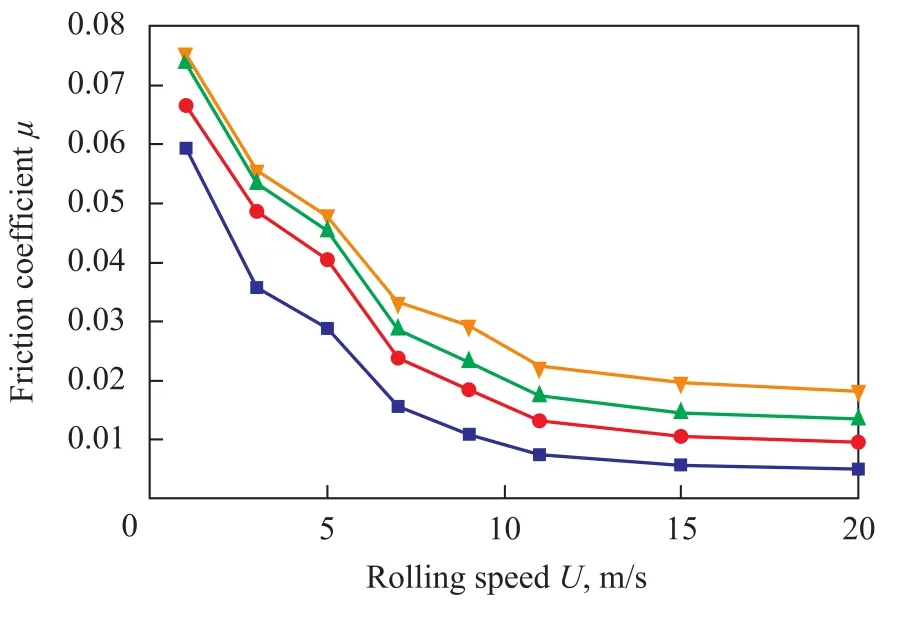
Figure 3 Variation in friction coefficient (µ) with rolling speed (U) at different ΔU when P0=1.2GPa , T=15 ℃

Figure 4 Variation in friction coefficient (µ) with rolling speed (U) at different ΔU when P0=1.35 GPa , T=15 ℃

It can be seen from Figures 5—7 that the friction coefficient increases with the increase in the sliding speed at different contact pressures. These curves have a common feature: the friction coef ficient increases linearly with the sliding speed when the sliding speed is low. A continuous increase in sliding speed gives rise to a progressive nonlinear increase in the friction coef ficient which, at a certain point, reaches a maximum value. The friction coef ficient is basically unchanged with a further increase in the sliding speed. The increase in the sliding speed can resultin an increase in the internal friction between the oil film layers, so the bigger the sliding speed is, the greater the friction coefficient would be. It also can be seen from Figures 5—7 that the larger the load is, the larger the friction coefficient would be. It shows that the oil is suitable for a low load. As it can be seen from Figures 5—7, the linear variation region at high rolling speed is wider than that at low rolling speed. When the rolling speed reaches 3 m/s, the friction coefficient increases linearly with the sliding speed rising from 0 to 0.05 m/s. When the rolling speed is 15 m/s, the friction coefficient increases linearly with the sliding speed increasing from 0 to 0.25 m/s.

Figure 5 Variation in friction coefficient (µ) with sliding speed (U) at different P0when T=15 ℃, U=3 m/s

Figure 6 Variation in friction coefficient (µ) with sliding speed (U) at different P0when T=15 ℃, U=7 m/s

Figure 7 Variation in friction coefficient (µ) with sliding speed (U) at different P0when T=15 ℃, U=15 m/s

3 Model for Calculation of Friction Coefficient

The apparently similar shapes of these experimental friction curves make it possible to relate the friction coeff icient (µ) against sliding speed (ΔU) by

whereAandBare the undetermined coefficients which vary with the operating conditions.

The coef ficientsAandBcan be obtained by a nonlinear regression analysis to minimize the squared deviation between the computed data and the corresponding experimental data. Upon using this method, each optimum solution of the coef ficientsAandBis obtained by a computer program at any given normal load and rolling speed.

It is noteworthy that the two coefficients,AandB, can be expressed by the non-dimensional variablesThese equations include:

P—Normal load;

E*—Equivalent modulus of elasticity;

R—Equivalent radius of curvature;

η0—Dynamic viscosity.

Fortunately, by taking logarithm on both sides, the ternary simple nonlinear equations can be transformed into linear ones. In a similar way, a linear regression analysis is performed. The fitting results are shown in Table 2.

According to the fitting results, the friction coefficient calculation formula can be obtained as follows:

Table 2 Regression of the coefficientsAandBin the fitting formula

It can be seen that the fits between the measured data and the values predicted by the formulae shown above is fairly good as evidenced by Figures 5—7, in which the lines represent the formulae predictions and the points represent the experimental data. The computed results show that the errors of the predicted results by the formulae relative to the measured data range from 1% to 10%. So the friction coefficient model can meet the needs of practical application.

4 Conclusions

The friction curves were obtained under sliding and rolling movements at point contact, by which the friction characteristics of a space lubricating oil No. 4129 were evaluated and analyzed. The bigger the load is, the larger the friction coefficient would be. The oil is suitable for the low load operating conditions.

The friction coefficient increases with the decrease in rolling speed. The rolling speed ranging from 1 m/s to 10 m/s has an important effect on the friction coefficient of the lubricating oil No. 4129. When the rolling speed surpasses 10 m/s, the friction coefficient keeps a constantly lower value with the increasing rolling speed. So the lubricating oil No. 4129 can adapt to applications at a rolling speed in excess of 10 m/s.

The friction coefficient increases linearly with the sliding speed when the sliding speed is low. A continuous increase in sliding speed gives rise to a progressive nonlinear increase in the friction coefficient. The friction coefficient is basically unchanged with a further increase in the sliding speed. The linear variation region of the friction coefficient versus sliding speed at high rolling speed is wider than that at low rolling speed.

The friction coefficient model is reasonable, and the correlation coefficient is greater than 0.9.

Acknowledgement:The Project is supported by the National Science Foundation of China (51105131) and the Excellent Youth Foundation of Henan Scientific Committee (12410050002) and the Creative Talent Foundation at Universities of Henan Province (2011HASTIT1016).

Reference

[1] Jia Chao, Guo Feng, Fu Zhongxue. Experimental study on the stribeck curve of EHL contacts under conditions of wall slippage[J]. Lubrication Engineering, 2010, 35(1): 33-36

[2] Guo Feng, Wong Pat Lam, Fu Zhongxue. Experiment observation of elastohydrodynamic lubrication films under conditions of wall slippage[J]. Chinese Journal of Mechanical Engineering, 2007, 43(10): 36-40 (in Chinese)

[3] Masayoshi Muraki, Eiji Tominaga. Friction properties of some additives for sliding guide way lubricants in a sliding speed range between 0.002 and 1.5 m/s with a thrust collar friction tester[J]. Tribology, 2001, 34: 437-442

[4] Pepper S V, Kingsbury E. Spiral orbit tribometry-Part I: Description of the tribometer[J]. Tribology Transaction, 2003, 46 (1): 57-64

[5] Pepper S V, Kingsbury E. Spiral orbit tribometry-Part II: Evaluation of the three liquid lubricants in vacuum[J]. Tribology Transaction, 2003, 46 (1): 65-69

[6] Lafountain A. R. and Johnston G. J. The elastohydrodynamic traction of synthetic base oil blends[J]. Tribology International, 2001, 4: 648-656

[7] Querlioz E., Ville F. and Lubrecht T. Experimental investigations on the contact fatigue life under starved conditions[J]. Tribology International, 2007, 40: 1619-1626

[8] Wang Yanshuang, Deng Sier, Yang Haisheng, et al. Analysis for traction characteristics of HKD aviation lubricating oil in rolling/sliding contacts[J]. Acta Armamentarii, 2009, 30(7): 958-961 (in Chinese)

[9] Meng Qingzhong, Yang Boyuan. The analysis of traction behavior of the new type high-speed aerial lubricating oil by the T-J model[J]. Machinery Design and Manufacture, 2006 (3): 9-11 (in Chinese)

[10] Chen Guoding, Wang Buying, Zhou Hong, et al. On the traction characteristics analysis of synthetic lubricants in rolling/sliding contacts[J]. Journal of Northwestern Polytechnical University, 1992, 10(3): 330-336

[11] Wang Yanshuang, Yang Boyuan. Investigation into the traction coefficient in elastohydrodynamic lubrication[J]. Tribotest Journal, 2004, 11(2): 113-124

[12] WANG Yan-shuang, YANG Bo-yuan, WANG Li-qin, et al. Traction Behavior of No. 4106 Aviation Lubricating Oil[J]. Tribology, 2004, 24(2): 156-159

Recieved date: 2013-11-29; Accepted date: 2014-03-17.

Wang Yanshuang, E-mail: hkd_wang_ yan_shuang@126.com.