连杆驱动的曲柄摇块机构综合设计的解析方法*

郑相周，罗红汉，傅国栋，李 慧

(1.华中农业大学 工学院, 湖北 武汉 430070； 2.华中农业大学 图书馆, 湖北 武汉 430070)

连杆驱动的曲柄摇块机构综合设计的解析方法*

郑相周1，罗红汉2，傅国栋1，李 慧1

(1.华中农业大学 工学院, 湖北 武汉 430070； 2.华中农业大学 图书馆, 湖北 武汉 430070)

曲柄摇块机构是一种应用广泛的典型的平面机构。将连杆作为主动件可使曲柄在一定角度范围内摆动。对于给定的曲柄摆动，有多种机构综合方法。笔者使用解析方法，以Jacob系数为指标对基于奇异构型、最大平均输出力矩和保证最小输出力矩等机构设计方法进行了分析和比较，使得能够更加深入地了解该机构的运动学特点，并为曲柄摇块机构的工程应用提供帮助。

曲柄摇块机构；机构综合；Jacob系数

Abstract: Based on criteria of maximum moment, crank rocker mechanisms driven by rocker with hydraulic cylinder are analyzed with analytical method in this paper. Optimized with this criteria, crank will output maximum moment when crank is in middle of its swing angle. The maximun average output moments in the crank swing scope will be got based on this criteria. The crank rocker mechanisms optimized with this criteria have a good force transmission ratio.

Key words: crank rocker mechanisms; mechanism synthesis; maximum output moment; force transmission ratio

0 引 言

曲柄摇块机构作为一种典型的平面机构，具有广泛的应用背景[1]。如图1所示，将连杆OB作为主动件，由移动副驱动。当连杆OB的长度变化时，曲柄BA在∠B1AB2范围内摆动。

图1 曲柄摇块机构

对于相同的曲柄摆动范围，使用不同的设计准则，可得到不同的构件尺寸，对应着不同的力学性能。压力角和传动角可用来表征曲柄摇块机构的传动特性分析[1]，但进行综合设计却不方便。笔者使用解析方法以Jacob系数为指标对基于奇异构型、最大平均输出力矩和保证最小输出力矩等机构设计方法进行分析和比较。

1 曲柄摇块机构Jacob系数

如图1，令l=OB，a=OA，r=AB。在△OAB中应用余弦定理，有:

a2+r2-2arcos (π-α)=l2

即:a2+r2+2arcosα=l2

(1)

式中：a、r均为常量。

对时间求导，并整理，得:

(2)

(3)

其中：

(4)

或者

(5)

令k=r/a，式(5)可写作为：

(6)

式(3)中负号表明当连杆伸长时，曲柄顺时针转动。式(3)表明了主动件运动速度到从动件运动速度的映射关系，J是速度变换系数，是Jacob矩阵在单自由度情形下的退化，称为Jacob系数。如果连杆中移动副的作用力为F，曲柄输出力矩为M，由静平衡下的虚功原理[4]有:

(7)

JM=F或者M=J-1F

(8)

显然，式(3)是机构主动力到输出力矩的映射。因此Jacob系数J不仅反映机构的运动关系也反映静力学关系。当J为0或∞时，机构均不可控；当J为除此之外的有限值时，其大小也反映驱动的速度和力变换情况，因此将VR=J称为速度变换系数，将FR=J-1称为力变换系数。Jacob系数J是机构力学性能的重要指标。

2 几种设计方法比较

对式(6)中α求导，有：

欲求J的极值，需解超越方程：3k+kcos 2α+2(1+k2)cosα=0。因此对机构进行运动或静力学优化设计，以J的极值作为目标几乎是不可能的，尤其是在工程应用中更加如此。

简而化之，从直观上提出了多种方法来进行曲柄摇块机构的综合，包括远离奇异构型、最大平均输出力矩和保证最小输出力矩方法等。

远离奇异构型设计方法以α=π/2处的曲柄作为摆角的角平分线，以使机构在运动过程中尽可能原理奇异构型；最大平均输出力矩方法将与连杆垂直的曲柄作为摆角的角平分线，曲柄在摆动范围内能够获得最大平均输出力矩；而保证最小输出力矩方法则使两个极限位置的连杆共线，可保证在两个极限位置处具有相同的输出力矩。这3种方法对应的机构综合简图如图2所示。

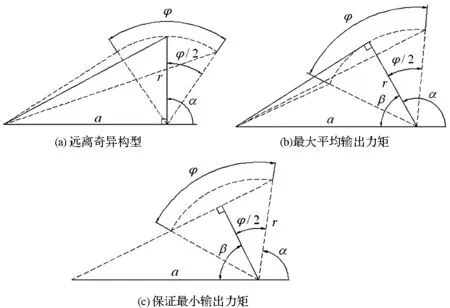
图2 曲柄摇块机构设计原则

给定曲柄摆角φ，可使用上述方法根据机构的几何特点确定构件尺寸a、r和连杆的行程。对应的方程如下：

(1) 远离奇异构型

(9)

(2) 最大平均输出力矩

(10)

(3) 保证最小输出力矩

(11)

式中：c为油缸结构参数[5]，L0为油缸行程，如图3。

图3 典型液压缸结构参数

这3种方法都需要根据应用要求先指定其中一个量，将该量作为参数再确定其他尺寸。它们的区别是，使用远离奇异构型和最大平均输出力矩需要用数值方法解非线性方程组，而保证最小输出力矩方法不需要解方程，仅使用代数方法就可得到结果。

对于所确定的机构性能优劣，可进一步使用Jacob系数来评价。在摆角范围内，Jacob系数使用式(5)或(6)计算，其中α值的变化范围表述如下：

(1) 远离奇异构型

(2) 最大平均输出力矩

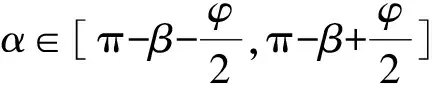
(3) 保证最小输出力矩

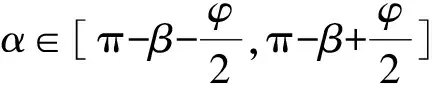
3 实例分析

某机械手中的一个关节采用曲柄摇块机构实现，连杆使用油缸驱动，油缸结构参数c=200。给定摆角φ=2π/3。在采用上述3种方法进行机构综合时，均给定曲柄长度，所得到的机构综合结果如表1。从表中知，这3种方法得到的构件尺寸只有微小的差别，其对应的Jacob系数及力传递率分别如图4和5所示。

表1 机构综合(r=70,φ=2π/3)

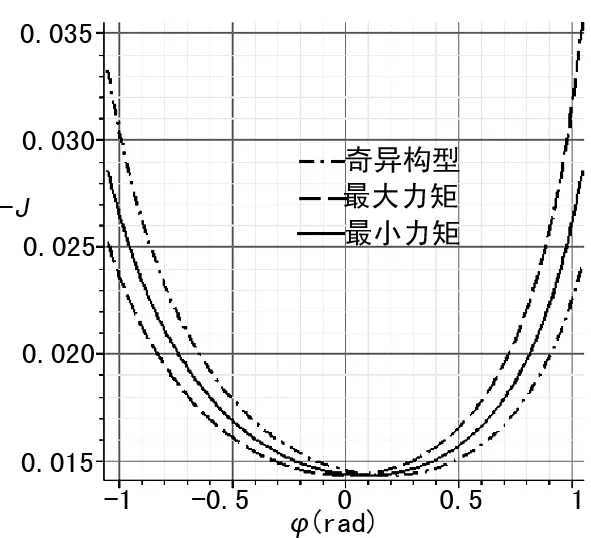
图4 Jacob系数

从图4、5可知，远离奇异构型和最大平均输出力矩方法使得Jacob系数在曲柄的两个极限位置有较大的差别，这会导致极限位置处的运动和受力有较大的变化；而保证最小输出力矩的方法在两个极限位置处的Jacob系数基本相同，有利于保证机构的工作性能。

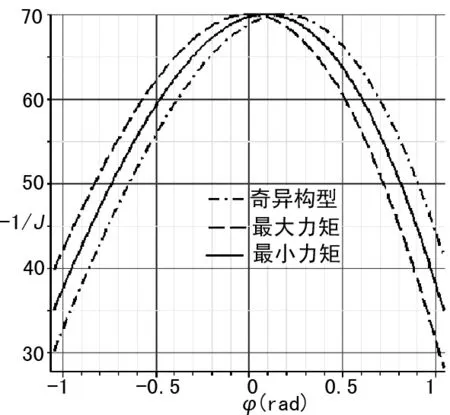
图5 力传递率

4 结 语

针对典型的以连杆为主动件、曲柄在一定范围内摆动的曲柄摇块机构，笔者使用Jacob系数对远离奇异构型、最大平均输出力矩和保证最小输出力矩3种设计方法进行了分析。分析结果表明，虽然3种方法得到的构件尺寸差别不大，但保证最小输出力矩设计方法可以使曲柄摇块机构的力学性能得到优化。使用保证最小输出力矩设计方法更便于工程设计。

[1] 彭文生，李志明，黄华梁. 机械设计[M]. 北京：高等教育出版社, 2002.

[2] Gosselin C, Angeles J. Singularity Analysis of Closed-loop Kinematic chains[J]. IEEE Transactions on Robotics and Automation, 1990,6(3):281-290.

[3] 郑相周,唐国元. 机械系统虚拟样机技术[M]. 北京：高等教育出版社, 2010.

[4] 程燕平. 理论力学[M]. 哈尔滨：哈尔滨工业大学出版社, 2008.

[5] 许福玲,陈尧明. 液压与气压传动[M]. 北京：机械工业出版社, 2008.

Analytical Synthesis Methods of Crank Rocker Mechanisms

ZHENG Xiang-zhou1, LUO Hong-han2, FU Guo-dong1, LI Hui1

( 1.SchoolofEngineering,HuazhongAgriculturalUniversity,WuhanHubei430010,China; 2.LibraryofHuazhongAgriculturalUniversity,WuhanHubei430010,China)

2014-07-03

郑相周(1963-)，男，河南温县人，副教授，博士，研究方向：先进制造技术和多体系理论。

TH111

A

1007-4414(2014)04-0018-03